Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Сформулируйте правило Лопиталя раскрытия неопределенностей. Объясните его применение при вычислении пределов функций в случаях разных видов неопределенностей.Неопределенность вида 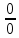 1)функции f (x) и g(x)и определены в промежутке [a, b) 2) 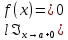 . . 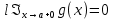 3) cуществуют в промежутке [a, b) конечные производные f ‘(x) и g’(x) 4) существует (конечный или бесконечный) предел 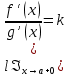 Тогда существует Тогда существует 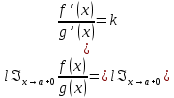 Пример 1: 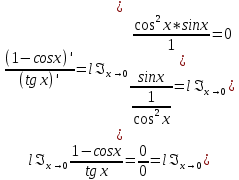 Неопределенность вида 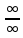 1)функции f (x) и g(x)и определены в промежутке [a, b) 2) 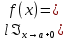 ∞. ∞. 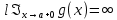 3) cуществуют в промежутке [a, b) конечные производные f ‘(x) и g’(x) , причем g’(x)≠0 ; 4) существует (конечный или бесконечный) предел 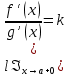 Тогда и Тогда и 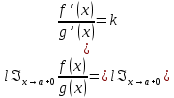 Пример 1 : 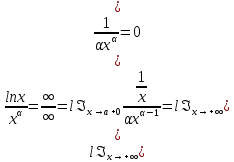 (α >0) Другие виды неопределенностей (0*∞), 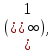 ( (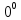 ), ), 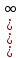 ) )При раскрытии других видов неопределенностей следует сначала свести  их к виду 0 их к виду 00 или ∞, а затем применить правило Лопиталя.  Приведите вывод формулы Тейлора для произвольной функции с остаточным членом в форме Лагранжа. Объясните получение формулы Маклорена.Rn(x)- остаточный члент формулы Тейлора Пусть f(x) – дифф-ма в т. x0 и имеет производные до порядка (n+1) включительно, тогда : Rn(x)= 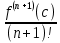 * (x-x0)n+1 – остаточный член ϕ1 в формуле Лагранжа * (x-x0)n+1 – остаточный член ϕ1 в формуле ЛагранжаС-точка между x и x0 f(x)=f(x0) + 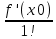 (x- x0) + (x- x0) + 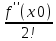 (x- x0)2 +…+ (x- x0)2 +…+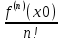 (x- x0)n + (x- x0)n + 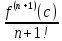 (x- x0)n+1 - формула Тейлора с остаточным членом в форме Лагранжа . (x- x0)n+1 - формула Тейлора с остаточным членом в форме Лагранжа .Pn(x)=Pn(0) + 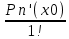 (x- x0) + (x- x0) + 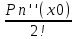 (x- x0)2 +…+ (x- x0)2 +…+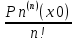 (x- x0)n - формула Тейлора для многочлена. (x- x0)n - формула Тейлора для многочлена.Если x0=0, то получаем Pn(x)=Pn(0) + 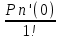 x + x + 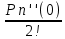 x2 +…+ x2 +…+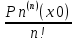 xn xnОбъясните разложение основных элементарных функций (𝑒𝑥, sin 𝑥, cos 𝑥, ln 𝑥, 𝑎rctg 𝑥) по формуле Маклорена.f(x)=ex. Так как f(x)=f '(x)= f '' (x)=…= f(n+1)(x)=ex ; f(0)=f '(0)= f '' (0)=…= f(n+1)(0)=1, то формула Маклорена имеет вид 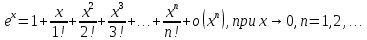 f(x)=sinx. Так как f(n)(x)=sin(x+n 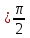 ); f(n)(0)=sin(n ); f(n)(0)=sin(n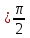 )= )=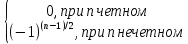 , то формула Маклорена имеет вид sinx= , то формула Маклорена имеет вид sinx=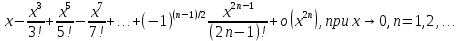 f(x)=cosx. Так как f(n)(x)=cos(x+n 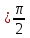 ); f(n)(0)=cos(n ); f(n)(0)=cos(n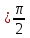 )= )=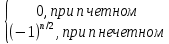 , то формула Маклорена имеет вид cosx= , то формула Маклорена имеет вид cosx=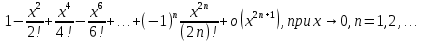 f(x)=ln(1+x). Так как f(n)(x)= 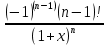 ; f(n)(0)= ; f(n)(0)=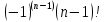 , то формула Маклорена имеет вид ln(1+x)= , то формула Маклорена имеет вид ln(1+x)=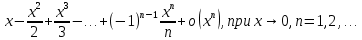 f(x)=arctgx, то формула Маклорена имеет вид arctgx= 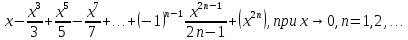 |
