Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Сформулируйте и докажите теорему о среднем значении для интеграла Римана, приведите её геометрическую интерпретацию.Теорема: Теорема о среднем. Если функция f(x) непрерывна на [a,b], то существует такая точка ξ ∈[a,b], что 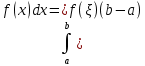 , , 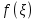 - среднее значение функции на отрезке - среднее значение функции на отрезкеДоказательство: Пусть a ≤ 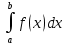 ≤ М ≤ М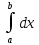 m 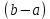 ≤ ≤ 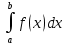 ≤ М ≤ М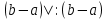 m≤ 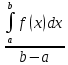 ≤ М ≤ Мm≤ η ≤ М Между наименьшим и наибольшими значениями функции по т.Коши о промежуточных значениях функции обязательно найдется ξ ∈[a,b]= η f(ξ )= 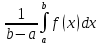 , следовательно , следовательно 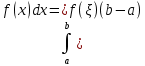 Геометрически: для площади криволинейной трапеции ограниченной сверху непрерывной кривой всегда существует равновеликий ей прямоугольник с тем же основание, а высота его равна одной из ординат этой кривой. Введите понятие определенного интеграла с переменным верхним пределом. Сформулируйте его свойства и одно из них докажите.Пусть функция f(x) интегрируема на отрезке [a, b],тогда по свойству 3 она интегрируема и на любом отрезке [a, х], где  Функция F определена на отрезке [a, b] и называется интегралом с переменным верхним пределом. Геометрически функция F(х) представляет собой площадь заштрихованной криволинейной трапеции , если F(х)>0.  Свойства интеграла с переменным верхним пределом. Теорема 1. Пусть интегрируема на Доказательство. Пусть Функция ограничена на Следовательно Теорема 2. Пусть функция интегрируема на Теорема 3.Пусть функция непрерывна на |
