Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Опишите понятия верхней и нижней сумм Дарбу. Сформулируйте их свойства. Введите понятия верхнего и нижнего интегралов Дарбу. Сформулируйте критерий интегрируемости Дарбу.Пусть f(x) определена и непрерывна на отрезке [a,b]. Пусть 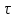 – некоторое разбиение отрезка [a,b] точками – некоторое разбиение отрезка [a,b] точками 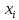 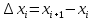 , i=0,1,2,... n-1 , i=0,1,2,... n-1Тогда по теореме Вейерштрасса f(x) ограничена на [a,b] и достигает на нем своей верхней и нижней граней, а значит она ограничена и на любом частичном отрезке [ 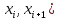 разбиения. разбиения.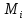 =sup f(x), =sup f(x), 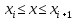 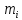 = inf f(x), = inf f(x), 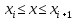 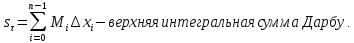 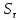 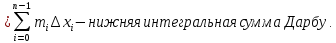 Свойства: 1. Если f-ограничена, то при любом разбиение 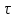 суммы, суммы, 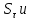 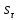 определена. определена.2.Для любого разбиения 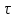 при любом выборе точек при любом выборе точек 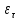 на [ на [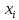 , , 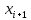 ] ]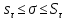 3. Если 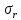 –какая-либо интегральная сумма Римана, соответствующая разбиению –какая-либо интегральная сумма Римана, соответствующая разбиению 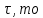 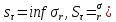 4. При измельчении разбиения верхняя сумма Дарбу не возрастает, а нижняя сумма не убывает. 5. 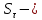 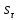 = = 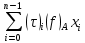 , где , где 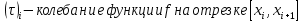 Множество{S} всех верхних сумм Дарбу отвечающих разбиению 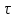 на отрезке ограничено снизу, а множество всех нижних сумм Дарбу ограничено сверху. на отрезке ограничено снизу, а множество всех нижних сумм Дарбу ограничено сверху.Таким образом, существует точная нижняя грань множества всех верхних сумм и точная верхняя грань  = inf = inf 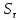 , , 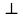 = sup = sup 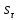  – верхний интеграл Дарбу – верхний интеграл Дарбу 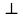 – нижний интеграл Дарбу. – нижний интеграл Дарбу.Теорема (Критерий Дарбу) Для того, чтобы существовал интергал от функции на необходимо и достаточно, чтобы были равны верхний и нижний интегралы дарбу 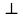 = = . При этом I= . При этом I=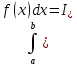 = = 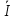 Сформулируйте критерий интегрируемости по Риману и следствие из него. Сформулируйте и докажите интегрируемость по Риману функции, непрерывной на отрезке и функции, монотонной на отрезке.Теорема (Критерий Римана) Для того чтобы ограниченная на отрезке (а,b), функция была интегрируема (по Риману) на этом отрезке, необходимо и достаточно, чтобы  Следствие. Если функция f интегрируема, то не только ее интегральные суммы Римана, но также и интегральные суммы Дарбу стремятся к ее интегралу, когда мелкость разбиения λ стремится к нулю. Теорема. Если функция f(х) непрерывна на отрезке (a,b), то она интегрируема на этом отрезке. Доказательство. Ограниченность По теореме Кантора эта функция равномерно непрерывна на отрезке . Значит, для любого найдется такое , что для любых и , принадлежащих отрезку , из неравенства следует неравенство Возьмем такое разбиение Отсюда следует, что Значит, Теорема. Если функция f(х), монотонна на отрезке (a,b), то она интегрируема на этом отрезке. Доказательство. Ограниченность на отрезке следует из свойств непрерывных функций. Пусть возрастает на отрезке , т.е. В силу монотонности имеем Тогда
Свойства определенного интеграла: Для любой функции f положим по определению: 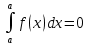 , а для функции, интегрируемой на отрезка [a,b]: , а для функции, интегрируемой на отрезка [a,b]: 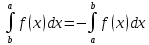 , a , a 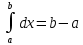 Если функция f(x) интегрируема на [a,b], то она интегрируема на [с,d] ⊂[a,b] Аддитивность. Пусть a Постоянный множитель можно вынести за знак определённого интеграла 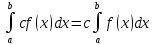 Определенный интеграл от алгебраической суммы равен алгебраической сумме их интегралов Если функция f(x) интегрируема на [a,b], неотрицательна(f(x) ≥0) и a Если функции f и g интегрируемы на [a,b], для всех x∈[a,b] f(x) ≥g(x), то 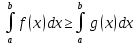 , то ест неравенство можно почленно интегрировать , то ест неравенство можно почленно интегрироватьЕсли функция f(x) интегрируема на [a,b], a Если функция f(x) интегрируема на [a,b], a f(x) 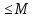 для любого x из [a,b], то для любого x из [a,b], то m(b-a) 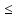 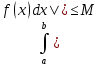 (b-a). Следствие: Если во всем промежутке имеет место неравенство (b-a). Следствие: Если во всем промежутке имеет место неравенство 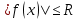 , то | , то |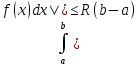 Пусть функция y=f(x) определена на отрезке [-a,a] и четна на этом отрезке. Тогда ее график симметричен относительно оси Oy. Если функция y=f(x) непрерывна на отрезке [-a,a] и является четной, то 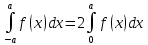 Пусть функция y=f(x) определена на отрезке [-a,a] и нечетна на этом отрезке. Тогда ее график симметричен относительно оси начала координат. Если функция y=f(x) непрерывна на отрезке [-a,a] и является нечетной, то 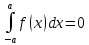 |
