Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Сформулируйте и докажите достаточное условие существования экстремума в терминах второй производной. Опишите условия его применимости и проиллюстрируйте на примере.В случае когда исследование знака I-ой производной слева и справа от точки x0 (возможного экстремума) затруднено, целесообразно использовать 2-ое достаточное условие , которое предполагает существование в точке x0 , конечной II-ой прозводной, отличной от нуля. Теорема (Второе дост-ое усл-е экстремума в терминах второй пр-ой): 1) Пусть x0 - стац. точка f(x), т.е. f ′ (x0) = 0 2) f(x) имеет в т. x0 конечную 2-ую производную f ′′ (x0), тогда если f ′′ (x0) < 0, то в т. x0 имеем максимум, а если f ′′ (x0) > 0 , то минимум Док-во: По опр-ю производной имеем:f ′′ (x0) = 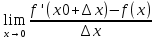 = = 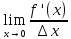 = = 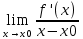 1) По условию f ′′ (x0) > 0 , функция ( по теореме о пределах) приобретает знак своего предела, то есть функция 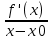 приобретает знак своего предела,то есть знак f ′′ (x0) . f ′′ (x0) > 0 ,тогда приобретает знак своего предела,то есть знак f ′′ (x0) . f ′′ (x0) > 0 ,тогда 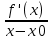 , слева от т x0 , x-x0 <0, тогда f ′ (x) должно быть меньше 0, чтобы , слева от т x0 , x-x0 <0, тогда f ′ (x) должно быть меньше 0, чтобы 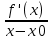 > 0 . Справа от т. x0 , x - x0 >0 , тогда f ′ (x) должна быть больше 0 , чтобы > 0 . Справа от т. x0 , x - x0 >0 , тогда f ′ (x) должна быть больше 0 , чтобы 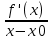 > 0 → (по теореме 3) в т. х0 имеем минимум. ч.т. д. > 0 → (по теореме 3) в т. х0 имеем минимум. ч.т. д.Правило Если f ′′ (x0) > 0 , то имеем в т. х0 -минимум, а если f ′′ (x0) < 0 , то имеем в т. х0 -максимум Это правило имеет более узкий круг применения. Оно не применимо к тем точкам, где не существует I-ой конечной производной. Не применимо к тем точкам , где II-ая производная равна нулю. Сформулируйте теорему, выражающую достаточные условия экстремума функции, не дифференцируемой в данной точке. Приведите пример.Экстремум функции, не дифференцир-ой в данной точке Теорема 5. Пусть f(x) дифференц-ма всюду в некоторой окрестности т х0 , кроме самой т. х0, в которой она однако непрерывна. Тогда,если слева от т. х0 f ′ (x) > 0 (соответственно f ′ (x) < 0 ), а справа от т. х0 f ′ (x) < 0 (соответственно f ′ (x) > 0 ), то т. х0  максимум (соотв-но минимум). максимум (соотв-но минимум).Пример 1. у= ǀ х ǀ - исследовать на экстремум. 1) х >0 , y= x, тогда у′ =1 > 0 (справа от т. 0 ) 2) x<0 , y= -x, тогда у′ = - 1 < 0 (слева от т. 0 ) (по теореме 5) в т. х0 = 0 у = ǀ х ǀ - имеет минимум
Пусть f(x) определена в некоторой окрестности точки х0, тогда точка х0 называется точкой возрастания(убывания) функции, если существует такое δ>0 что при х0- δ<x<x0 (т.е. слева от точки х0) f(x)>f(x0), а справа от т.х0 при х0<x<x0+ δ f(x)<f(x0), Точка возрастания -характеризуется тем, что при переходе через неё приращение функции  f меняет знак с - на + . Точка убывания с + на - f меняет знак с - на + . Точка убывания с + на - Достаточные условия экстремума в терминах высших производных Пусть в т. х0 у функции f(x) существуют все производные до порядка n включительно, причем: f ′ (x0) = f ′′ (x0) = f ′′′ (x0) = ... = f(n-1) (x0 ) = 0 , a f(n) (x0 ) 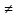 0 0 Тогда, если n - четное, то в т. х0 есть экстремум, а именно если f(2k) (x0 ) > 0 , то минимум , а если f(2k) (x0 ) < 0 , то максимум. Если n – нечетное, то в т. х0 экстремума нет, а т. х0 будет точкой возрастания (убывания), если f 2k+1 (x0 ) > 0 (f 2k+1 (x0 ) < 0 ) Если f ′ (x0 ) > 0, то х0 является точкой возрастания функции. Если f ′ (x0 ) < 0, то х0 являыется точкой убывания функции. Если f ′ (x0 ) = 0, а f ′′ (x0 ) 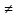 0 , то в т. х0 есть экстремум, а именно, если f ′′ (x0 ) > 0 , то минимум. 0 , то в т. х0 есть экстремум, а именно, если f ′′ (x0 ) > 0 , то минимум.Пример: f(x) = 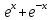 + 2 cos x - исследовать на экстремум + 2 cos x - исследовать на экстремумРешение: 1) f ′ (x) = 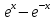 + 2 sin x = + 2 sin x = 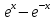 - 2 sin x - 2 sin x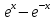 - 2 sin x = 0 x0 = 0 - стационарная точка - 2 sin x = 0 x0 = 0 - стационарная точка2)f ′′ (x) = 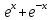 - 2 cos x , f ′′ (x0 ) = 0 - 2 cos x , f ′′ (x0 ) = 03)f ′′′ (x) = 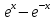 + 2 sin x , f ′′′ (x0 ) = 0 + 2 sin x , f ′′′ (x0 ) = 04)f ′′′′ (x) = 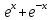 + 2 cos x f ′′′′ (x0 ) = 4 > 0 → по теореме 6 х0 - точка минимума. + 2 cos x f ′′′′ (x0 ) = 4 > 0 → по теореме 6 х0 - точка минимума. |
