Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Введите понятие монотонной функции. Сформулируйте и докажите признак монотонности функции, объясните его геометрический смысл. Проиллюстрируйте его применение на конкретном примере.Функция называется монотонной на промежутке, если она на этом промежутке или возрастает, или убывает. Функция называется монотонной на какой-то области, если ее приращение не меняет знак и остается постоянным (по знаку) всегда на этой области. Признак монотонности. Пусть функция f(x): непрерывна на некотором промежутке x с концами a и b; дифференцируема во всех внутренних точках (a, b) тогда для того чтобы y=f(x) возрастала(убывала) ⇔чтобы f ’(x) ≥0 (неотрицательна) (f ’(x) 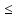 0 (неположительна)) во всех внутренних точках промежутка x на (a,b). Если во всех внутренних точках x f ’(x)>0(f ’(x)<0), то f(x)- строго возрастает(убывает). 0 (неположительна)) во всех внутренних точках промежутка x на (a,b). Если во всех внутренних точках x f ’(x)>0(f ’(x)<0), то f(x)- строго возрастает(убывает).Доказательство: 1. Необходимость. Пусть f(x) возрастает(убывает) на х с концами (a,b). По определению, если х1< х2, то f(х1)< f(х2). Пусть х0∈Х, возьмем ∆х такое, что ∆х>0 и U(x0+∆х) ∈Х ⇒ x0+∆х>х⇒ т.к. f(x)-возрастает(убывает), то f(x0+∆х)-f(x0)>0 (f(x0+∆х)-f(x0)<0). Рассмотрим отношение 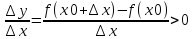 ( (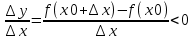 ). ). Переходя к пределу имеем 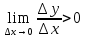 ⇒f ’(x)>0( ⇒f ’(x)>0(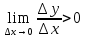 ⇒f ’(x)<0) чтд. ⇒f ’(x)<0) чтд.2. Достаточность. Пусть х1< х2 , х1 и х2∈Х, тогда по формуле Лагранжа имеем: f(x2)- f(x1)=f ’( 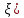 ( х2 -х1). Нам дано f ’(x) ≥0 ⇒ f ’( ( х2 -х1). Нам дано f ’(x) ≥0 ⇒ f ’(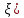 ≥0 ⇒ f(x2)- f(x1) ≥0 ⇒ f(x2) ≥f(x1) ⇒ f(x)-возрастает на Х.(аналогично f ’(x) ≥0 ⇒ f(x2)- f(x1) ≥0 ⇒ f(x2) ≥f(x1) ⇒ f(x)-возрастает на Х.(аналогично f ’(x) 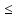 0) 0)Если f ’(x) 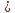 0 ⇒ f ’( 0 ⇒ f ’(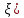 >0 ⇒ f(x2)- f(x1) >0 ⇒ f(x2) >f(x1) ⇒ f(x)-строго возрастает на Х. (аналогично f ’(x) >0 ⇒ f(x2)- f(x1) >0 ⇒ f(x2) >f(x1) ⇒ f(x)-строго возрастает на Х. (аналогично f ’(x) 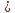 0) 0)f (x) –возрастает (угол острый) f (x) –убывает (угол тупой)
Пусть функция определена в некоторой окрестности точки х0. Тогда х0 называется точкой максимума(минимума) функции если существует δ окрестность точки х0(х0-δ, х0+δ), такая, что для любого x∈(х0-δ, х0+δ) выполняется неравенство f ’(x) 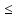 f(x0) (соответственно f ’(x) ≥f(x0)). f(x0) (соответственно f ’(x) ≥f(x0)).Точки минимума и максимума называются точками экстремума. Необходимое условие экстремума. Пусть х0 является точкой экстремума функции f, определенной в некоторой окрестности точки х0. Тогда либо производная f ’(x) не существует, либо равна 0. Достаточное условие экстремума. Пусть точка х0 является точкой возможного экстремума(критической). f(x) дифференцируема всюду в некоторой окрестности точки х0. Тогда если в этой окрестности слева от точки х0 выполняется неравенство f ’(x)>0 а справа f ’(x)<0, то в точке х0 функция имеет максиму, а если при х0-δ< х<x0 выполняется неравенство f ’(x)<0, а при х0 < х<x0+δ неравенство f ’(x)>0, то х точка минимума. Доказательство(для максимума): Пусть f ’(x)>0 при x∈(х0-δ, х0) и f ’(x)<0 при x∈(х0, х0+δ). Надо доказать, что f ’(x)-наибольшее значение в окрестности x0. Достаточно доказать, что f(x0)-f(x)>0 при любых х∈(х0-δ, х0+δ). Функция дифференцируема в U(х0,δ) ⇒непрерывна в U(х0,δ) и в частности на [x0,x]. f(x0)-f(x)= f ’( 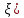 ( х0 -х) ⇒ f(x0)-f(x)>0, т.е. f(x0) >f(x), т.е. f(x0)- наибольшее значение(максимум). ( х0 -х) ⇒ f(x0)-f(x)>0, т.е. f(x0) >f(x), т.е. f(x0)- наибольшее значение(максимум).Если f ’(x) не меняет знак f(x0)-f(x)= f ’( 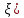 ( х0 -х) -( х0-δ, х0) ⇒ f(x0) >f(x) ( х0 -х) -( х0-δ, х0) ⇒ f(x0) >f(x)f(x0)-f(x)= f ’( 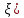 ( х0 -х) -( х0,х0+δ) ⇒ f(x0) ( х0 -х) -( х0,х0+δ) ⇒ f(x0) |
