Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Сформулируйте и докажите достаточные условия перегиба графика функции в терминах второй производной и в терминах третьей производной. Проиллюстрируйте их на примерах.Теорема (первое достаточное условие точки перегиба). Пусть функция y=f(x) имеет вторую производную в некоторой окрестности точки х0 и f’’(x0)=0. Тогда, если в пределах указанной окрестности вторая производная f’’(x0)=0 имеет разные знаки слева и справа от x0, то график этой функции имеет перегиб в точке М(х0,f(x0)). Теорема. (второе достаточное условие точки перегиба в терминах третьей производной).Если функция y=f(x) имеет в точке х0 конечную третью производную и при этом 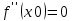 а а 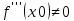 , то график этой функции имеет перегиб в точке M(x0,f(x0)) , то график этой функции имеет перегиб в точке M(x0,f(x0))Доказательство: Пусть 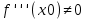 пусть пусть 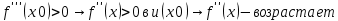 Так как 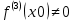 то по теореме о строгом возрастании (убывании) функции то по теореме о строгом возрастании (убывании) функции 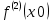 либо строго возрастает, либо строго убывает в точке х0 . По условию либо строго возрастает, либо строго убывает в точке х0 . По условию 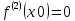 поэтому поэтому 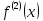 имеет разные знаки на интервалах имеет разные знаки на интервалах 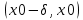 и и 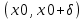 при некотором при некотором 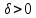 откуда используя теорему о первом достаточном условии наличия точек перегиба, заключаем что х0 точка перегиба функции f(x). откуда используя теорему о первом достаточном условии наличия точек перегиба, заключаем что х0 точка перегиба функции f(x).
Говорят, что х=а является вертикальной асимптотой графика функции у=f(x), если хотя бы один из пределов 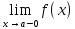 или или 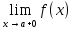 был равен был равен 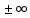 . .Говорят, что прямая у=kx+b является наклонной асимптотой графика функции у=f(x) при х 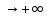 , если f(x) представима в виде: f(x)=kx+b+ , если f(x) представима в виде: f(x)=kx+b+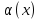 , где , где 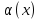 , бесконечно-малая функция, т.е , бесконечно-малая функция, т.е 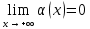 . .Теорема (о существовании наклонной асимптоты) Для того чтобы график функции у=f(x) имел при х 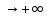 наклонную асимптоту необходимо и достаточно, чтобы существовали два предела: наклонную асимптоту необходимо и достаточно, чтобы существовали два предела: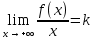 (1) (1)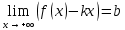 (2) (2)Доказательство: Необходимость. Пусть график функции у=f(x) имеет наклонную асимптоту. Нужно доказать, что существуют два предела (1) и (2). По определению наклонной асимптоты имеем: f(x)=kx+b+ 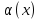 , где , где 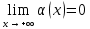 . Найдем: . Найдем: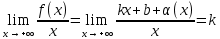 (1) (1)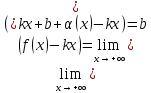 (2) (2)Достаточность. Даны два предела (1) и (2). Нужно доказать, что f(x)=kx+b+ 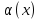 . Из (2) . Из (2)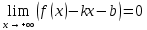 , означает что , означает что 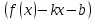 – бесконечно малая функция. Обозначим ее через – бесконечно малая функция. Обозначим ее через 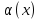 = =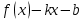 . Следовательно, f(x)=kx+b+ . Следовательно, f(x)=kx+b+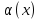 , откуда следует, что у=f(x) – имеет наклонную асимптоту. , откуда следует, что у=f(x) – имеет наклонную асимптоту. Опишите схему полного исследования функции с помощью производной и построения её графика. Схему полного исследования функции с помощью производной и построения её графика. Найти область определения ф-ции и, если возможно, область изменения ф-ции. Исследовать ф-цию на четность, нечетность, периодичность. Найти точки пересечения графика ф-ции с осями координат и интервалы знакопостоянства ф-цию. Исследовать функцию на непрерывность. Найти точки разрыва (если они существуют) и установить их характер. Исследовать поведение ф-ции на концах области определения. Определить интервалы монотонности (возрастания и убывания) ф-ции: найти точки экстремума и ф-ции. Определить интервалы выпуклости вниз и выпуклости вверх графика ф-ции; найти точки перегиба и значения ф-ции в этих точках. Найти асимптоты графика ф-ции (вертикальные, горизонтальные, наклонные y=kx+b) 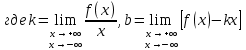 Взять несколько контрольных точек. Построить график ф-ции.
Пусть в некоторой окрестности точки (х0,y0,z0) задана функция u=u(х,y,z), фиксируя переменные y и z: y=y0, z=z0 , получим функцию одной переменной х: u=u(х,y0,z0). Обычная производная этой функции по х в точке х0 называется частной производной функции. 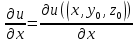 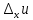 = u(x0+ = u(x0+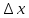 , y0,z0)-u(х0,y0,z0) – приращение функции u по переменной x , y0,z0)-u(х0,y0,z0) – приращение функции u по переменной x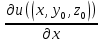 = =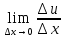 Пусть u=u(х,y,z), тогда выражение вида 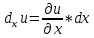 – называется частным дифференциалом функции u по переменной x. – называется частным дифференциалом функции u по переменной x.Сумма всех частных дифференциалов функции– называется полным дифференциалом функции: du= 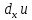 + +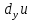 + +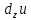 . .Примеры: Частные производные: u= 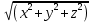 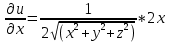 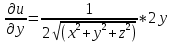 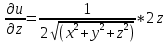 Частные дифференциалы: все тоже самое, умноженное на dx. |
