Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Введите понятие частных производных второго и третьего порядков (чистых и смешанных). Приведите примеры нахождения частных производных второго и третьего порядков.Пусть задана функция f(х,y,z), найдем ее частные производные: 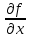 , , 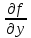 , ,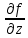 , тогда выражение вида : , тогда выражение вида : 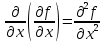 –называется чистой частной производной второго порядка, –называется чистой частной производной второго порядка, 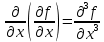 – чистая частная производная третьего порядка. – чистая частная производная третьего порядка.Пусть задана функция f(х,y,z), найдем ее частные производные: 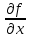 , , 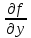 , ,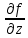 , тогда выражение вида: , тогда выражение вида: 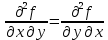 – называется смешанной частной производной второго порядка, – называется смешанной частной производной второго порядка, 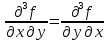 – смешанная частная производная третьего порядка. – смешанная частная производная третьего порядка.Примеры: f(x,y,z)= 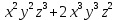 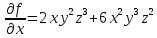 – частная производная по Х. – частная производная по Х.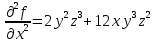 – частная производная второго порядка по Х. – частная производная второго порядка по Х.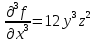 – частная производная третьего порядка по Х. – частная производная третьего порядка по Х.Сформулируйте теорему о равенстве смешанных частных производных второго порядка. Приведите примеры.Теорема (о равенстве смешанных производных) Пусть f(x.y) – определена вместе со своими частными производными 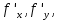 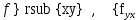 в некоторой окрестности точки (х0,у0), причем в некоторой окрестности точки (х0,у0), причем 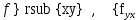 непрерывны в этой точке, тогда: непрерывны в этой точке, тогда: 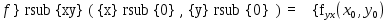 . .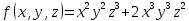 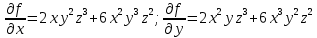 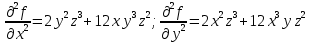 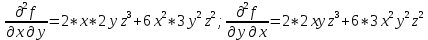 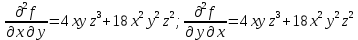 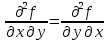
Дифференциалом функции z=f(x,y) называется сумма произведений частных производных этой функции на приращения независимых переменных Функция z=f(x,y) называется дифференцируемойой в точке (х,у), если ее полное приращение может быть представлено в виде Дифференциалом 2го порядка функции z=f(x,y) называют дифференциал от дифференциала 1го порядка. 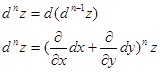 Рассмотрим сложную функцию у=f(u) , u=u(x), то есть у= f(u(х))= f(х). Тогда по определению дифференциала имеем dy=fх’(x)dx. Но поскольку производная сложной функции равна fх’= fu’*ux’,то dy= fu’ *ux’ dx. Используя равенство ux’ dx=du, получим dy= fu’(u) du. Сформулируйте необходимые условия существования экстремума функции двух переменных в точке. Опишите достаточные условия строгого экстремума функции двух переменных в точке. Объясните алгоритм нахождения экстремума функции двух переменных в точке. Необходимое условие экстремума. Если точка Введем обозначения Достаточное условие экстремума. Пусть функция 1) если то точка 2) если то в точке 3) если то экстремум может быть, а может и не быть. Шаг 1. Находим частные производные 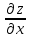 и и 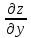 Шаг 2. Составляем систему уравнений из равенств этих производных нулю (их равенство нулю и есть необходимый признак существования экстремума): 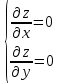 Решения этой системы уравнений (xk: yk) являются точками возможного экстремума - критическими точками. Шаг 3. Пусть M0(x0; y0) является критической точкой, найденной на шаге 2. Чтобы убедиться, что в ней существует экстремум функции двух переменных, находим частные производные второго порядка 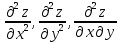 как частные производные от частных производных первого порядка, найденных на шаге 1. Шаг 4. Присваиваем частным производным второго порядка, найденным на шаге 3, буквенные обозначения: 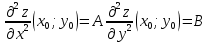 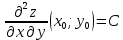 Находим определитель 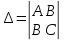 и проверяем достаточный признак существования экстремума. и проверяем достаточный признак существования экстремума.Если , 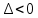 то экстремума в найденной критической точке нет, то экстремума в найденной критической точке нет,если 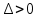 , то экстремум в найденной критической точке есть, , то экстремум в найденной критической точке есть,если 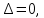 то то требуются дополнительные исследования. то то требуются дополнительные исследования.Если экстремум в найденной точке есть и если 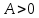 , то в этой точке существует минимум функции двух переменных, если , то в этой точке существует минимум функции двух переменных, если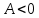 , то максимум. , то максимум.Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных z = z(x; y) и получаем значение экстремума функции двух переменных (минимума или максимума). Примеры начнём с более сложного, в котором составленная система уравнений имеет несколько решений, а, значит, найдено несколько критических точек.
Основная задача дифференциального исчисления: отыскание производной данной функции Дано: f(x). Найти: f ’(x) Обратная задача отыскание функции по ее производной (задача восстановления) Дано: F’(x). Найти: f(x), т.е. восстановить функцию по ее производной. Обратная задача к основной задаче является задачей дифференциального исчисления.
Пусть f(x) определена на некотором промежутке Е (конечный или бесконечный, замкнутый или незамкнутый).Тогда F(x) называется первообразной функцией для f(x) на Е, если F′ (x) = f(x). Основное свойство первообразных (2 формулировки). А) Любая первообразная для функции f(x) на промежутке Е может быть представлена в виде: F(x)+С. Доказательство. Пусть F(x)- первообразная f(x) →(по определению) F′(x)= f(x), пусть Ф(х)- первообразная f(x) →(по определению) Ф′ (x)= f(x). Докажем, что Ф(х)= F(x)+С. (Ф(х)– F(x))′ = Ф′ (х)– F′ (x)= f(x)– f(x)=0 Ф(х)– F(x)=С→ Ф(х)= F(x)+С ч.т.д. Б) Если в некотором Е функция f(x) имеет первообразную F(x), то F(x±С) – также является её первообразной. Доказательство. Пусть F(x)- первообразная f(x) →(по определению) F′ (x)= f(x). Проверим: (F(x)+С)′ = F′ (x)+C′= f(x)+0= f(x) ч.т.д. Правила нахождения первообразных. 1) Если F(x)- первообразная f(x), а G(x)- первообразная g(x), то (F(x)+ G(x)) – первообразная для (f(x)+ g(x)). (F(x)+ G(x))′ = F′ (x)+ G′ (x)= f(x)+g(x). 2) Если F(x)- первообразная f(x), а k – постоянная, то kF(x)- первообразная kf(x). 3) Если F(x)- первообразная f(x), а k, b – постоянные, причем k≠0, то 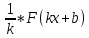 - первообразная для f(kx+b). - первообразная для f(kx+b). |
