Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Введите понятие неопределенного интеграла и объясните его геометрический смысл. Сформулируйте и докажите основные свойства неопределенного интеграла.Если F(x)-первообразная функции f(x) на промежутке Е, то F(x)+C, где С-произвольная постоянная называется неопределенным интегралом от функции f(x). 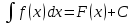 , где f(x)dx называется подынтегральным выражением, функция f(x) - подынтегральной функцией. , где f(x)dx называется подынтегральным выражением, функция f(x) - подынтегральной функцией.Геометрический смысл неопределенного интеграла Геометрически, неопределенный интеграл представляет собой семейство интегральных кривых на плоскости, полученных путем параллельного переноса графика функции y=f(x) вдоль оси ординат (рис. 3). Основные свойства неопределённого интеграла Свойство 1. Производная неопределенного интеграла равна подынтегральной функции: Доказательство. Свойство 2. Дифференциал неопределенного интеграла равен подынтегральному выражению: Доказательство. Свойство 3. Неопределенный интеграл от дифференциала функции равен этой функции плюс const: Доказательство. Свойство 4.Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от этих функций: Доказательство. пусть F(x) и G(x) – первообразные для функций f(x) и g(x) соответственно, т.е. Следовательно, 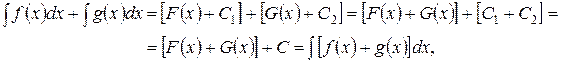 где – произвольная постоянная. Отметим, что данное свойство справедливо для любого конечного числа слагаемых функций. где – произвольная постоянная. Отметим, что данное свойство справедливо для любого конечного числа слагаемых функций.Свойство 5.Постоянный множитель можно выносить за знак интеграла: Доказательство. пусть F(x) – первообразная для функции f(x) , т.е. Отсюда следует, что
Интегрирование с помощью замены переменной (или интегрирование подстановкой). Теорема. Пусть функции f(u), и u = ϕ(x) определены на некоторых интервалах так, что имеет смысл сложная функция f(ϕ(x)) и функция ϕ(x) непрерывно дифференцируема. Тогда, если функция f(u) имеет первообразную F(u), то есть существует: ∫f(u)du =F(u) + C, то функция f(ϕ(x)) имеет первообразную F(ϕ(x)) и, значит, ∫ f(ϕ(x))*ϕ′(x)dx = F(ϕ(x)) + C. ∫ f(ϕ(x))*ϕ′(x)dx = ∫f(u)du – интегрирование подстановкой. 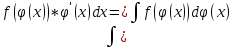 – формула подведения под знак дифференциала. – формула подведения под знак дифференциала.Интегрирование по частям. Теорема. Если функции u(x) и v(x) дифференцируемы на некотором промежутке и существует интеграл ∫u*du, то существует и интеграл ∫u*dv, справедливо равенство: ∫ u*dv = u*v− ∫ v*du Доказательство. Вычислим дифференциал произведения функций u(x)*v(x). d(u(x)*v(x)) = v(x)du(x) + u(x)dv(x) или u(x)dv(x) = d(u(x)*v(x))−v(x)du(x). Если дифференциалы функций равны, то, очевидно, их неопределенные интегралы, как множества функций, совпадают; поэтому ∫ u(x)dv(x) =∫ d(u(x)*v(x))− ∫ v(x)du(x). Основные группы интегралов, которые берутся посредством интегрирования по частям. 1 группа. Интегралы, подынтегральная функция которых в виде множителя содержит: ln x, arcsin x, arccos x, arctg x, arctg x2 и др., при этом оставшаяся часть функции является производной известной функции. 2 группа. 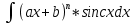 , ,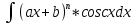 , , 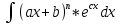 и др. За u=ax+b и путем n-кратного интегрирования по частям получаем результат. и др. За u=ax+b и путем n-кратного интегрирования по частям получаем результат.3 группа. 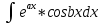 , ,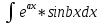 , ,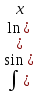 , ,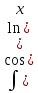 и др, берутся путем двухкратного интегрирования по частям и приведения интеграла к самому себе. и др, берутся путем двухкратного интегрирования по частям и приведения интеграла к самому себе.Обозначаем данный интеграл за I и интегрируем по частям. Приходим к линейному уравнению относительно I, решая его, находим I (приведение интеграла к самому себе).
Рациональной дробью с действительными(вещественными) коэффициентами называется отношение двух алгебраических многочленов Pn(x)/Qm(x) с действительными коэффициентами. Если n Элементарными дробями называются дроби 4 типов: 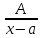 2) 2) 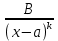 3) 3) 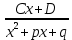 4) 4) 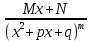 Теорема. Каждая правильная дробь может быть представлена в виде суммы конечного числа элементарных дробей. Метод неопределенных коэффициентов. Установить, что дробь правильная Если правильная разложить знаменатель Представить подынтегральную дробь в виде элементарных дробей с буквенными коэффициентами Привести к общему знаменателю и опустить его Приравнять коэффициенты при одинаковых степенях Подставить вместо А,B,C числа и проинтегрировать |
