Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Сформулируйте и докажите теорему, выражающую необходимые и достаточные условия дифференцируемости функции в точке.Теорема Для того чтобы функция f(x) была дифференцируемой в некоторой точке х0, необходимо и достаточно, чтобы функция f(x) имела в этой точке производную f’(x) и тогда: dy= f’(x)*dx. Доказательство: Необходимость. Пусть f(x) – дифференцируема в точке х0, тогда по определению: 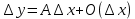 , , 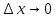 . Разделим обе части на . Разделим обе части на 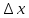 . . 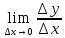 = =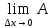 + +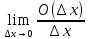 . .Следовательно f’(x0)=А+0, откуда f’(x)=А. Достаточность. Пусть f’(x0) =(по опр) 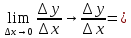 f’(x0)+ f’(x0)+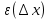 , где , где 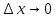 . .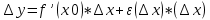 . Полагая, что . Полагая, что 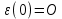 , получим , получим 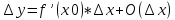 при при 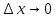 ., ., 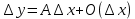 при при 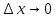 Следовательно f(x) дифференцируема в точке х0. Следовательно f(x) дифференцируема в точке х0.
Опр1. Если существует (конечный предел k(Δх)) 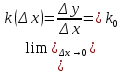 , то прямая определенная уравнением y=k0(x-x0)+y0 называется наклонной касательной к графику функции y=f(x) в точке x0. , то прямая определенная уравнением y=k0(x-x0)+y0 называется наклонной касательной к графику функции y=f(x) в точке x0.Уравнение касательной y=f’(x0)(x-x0)+f(x0) в случае конечной производной в точке. Если 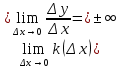 , то в этом случае существует вертикальная касательная х=х0. , то в этом случае существует вертикальная касательная х=х0.Опр2. Предельное положение секущей М0М при Δх→0 или, что то же при М→М0 называется касательной к графику функции f в точке М0. F’(х0)=tgφ – геометрический смысл производной в точке х0 есть tg угла, образованного касательной с положительным направлением оси Ох. Y=y0+f’(x0), (y0=f(x0)) – уравнение касательной y-y0=f’(x0) 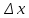 ( (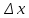 =dx) =dx)У-у0=dy – геометрический смысл дифференциала – это есть прирощение ординаты касательной, проведенной к графику функции в точке М0 с абсциссой х0. Физический смысл производной и дифференциала. 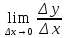 - скорость изменения одной переменной величины относительно другой (у относительно х) в точке х0. - скорость изменения одной переменной величины относительно другой (у относительно х) в точке х0.На интерпретации производной, как скорости изменения величины, относительно другой и основано в применении производной при изучении физических явлений и процессов. Дифференциал. Δу=А* Δх+0(Δх), Δх→0 У*у0 ≈dy 0(Δх)- погрешность Применение дифференциала функции в физике основано на том, что замена приращения функции дифференциалом позволяет заменить любую дифференцируемую в точке х0 функцию, линейной. |
