Mat_analiz_k_ekzamenu_Avtosokhranenny (копия). 9. Введите понятие производной второго, третьего и т д
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
Сформулируйте и докажите теорему, выражающую правила вычисления производной. Приведите примеры. Опишите свойства дифференциала функции.Теорема1. Пусть y1=f1(x) и y2=f2(x) – имеют производные в точке х0 и определены в U(x0), тогда у1+у2; у1*у2;у1/у2 также имеют производные в точке х0 и они равны. (y1+y2)’=y1’+y2’ (1) (y1*y2)’=y1’*y2+y1*y2’ (2) (y1|y2)’=(y1’*y2-y1*y2’)/у2 (3) Следствие 1. (с*у)’=c*y’ (4) Следствие 2. Пусть yk=fk(x) – имеют производные в точке х0, тогда производная линейной комбинации этих функций существует и она равна (с1у1+с2у2+…+сnyn)’=c1y1’+c2y2’+…+cnyn’ Доказательство: 1 часть. Пусть y1=f1(x), y2=f2(x) – определены в U(x0) и х0+Δс∈U(x0) Δy1=f1(x0+Δx)-f1(x0) Δy2=f2(x0+Δx)-f2(x0) 1)Если у=у1=у2 то Δу=(у1+Δу1+у2+Δу2)-(у1+у2)=Δу1+у2 Если Δх 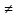 0, то разделим обе части на Δх. 0, то разделим обе части на Δх.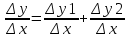 (переходя к пределу при Δх→0) (переходя к пределу при Δх→0)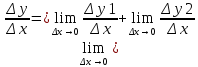 следовательно по определению y’=y1’+y2’, ч.т.д. следовательно по определению y’=y1’+y2’, ч.т.д.Пример. (tgx)’=( 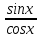 )’= )’=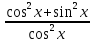 =1/cos2x =1/cos2xПравила вычисления дифференциалов. 1)d(y1+y2)=dy1+dy2 2)d(y1*y2)=y1dy2+y2dy1 3)d(c*y)=cdy 4)d(y1/y2)=(y2dy1-y1dy2)/y22 Доказательство: Пусть у=у1*у2 Dy=y’dx=(y1*y2)’dx=(y1’*y2+y1*y2’)dx=y2y1’dx+y1y2’dx=y2dy1+y1dy2
Теорема 2. Пусть f(x)=y – непрерывна и строго монотонна в некоторой окрестности точки х0 U(x0) и пусть при х=х0 существует производная 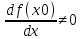 , тогда обратная функция x=f-1(y) имеет производную в точке у0=f(x0) и она равна , тогда обратная функция x=f-1(y) имеет производную в точке у0=f(x0) и она равна 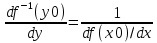 Теорема. Производная обратной функции равна обратной величине производной данной функции. Геометрический смысл теоремы. df(x0)/dx=tgα df-1(y0)/dy=tgβ,уголβ между касательной и осью Оу Β=π  /2-α /2-αdf-1(y0)/dy=tgβ=1/ctgβ=1/ctg( 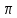 /2-α)=1/tgα=1/ /2-α)=1/tgα=1/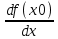 Пример. Y=arcsinx, x=siny, - π/2≤у≤π/2, -1≤х≤1 Применяя теорему 2 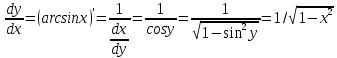 Y=arctgx, x=tgy, - π/2<у<π/2 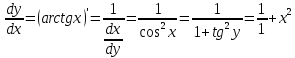 ч.т.д. ч.т.д.Сформулируйте теорему о производной сложной функции одной переменной. Приведите примеры её применения. Объясните инвариантность формы первого дифференциала.Теорема. Пусть у=f(x) имеет производную в т. x0, функция z=F(y) имеет производную в т. у0=f(x0) тогда сложная функция Ф(x)=F(f(x)) имеет производную при x=x0 и она равна Ф’(x0)=F'(y0) *f '(x0) Ф'(x0)=F'(f '(x0)) *f '(x0) 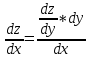 Пример: y=ex2, y’= ex2*(x2)’= ex2* 2x Следствие (инвариантность формы первого дифференциала относительно преобразования независимой переменной). dz=F’(y0)dy= Ф'(x0)dx. В этой формуле dy=f ’(x)dx является дифференциалом функции, а dx функцией независимой переменной. Таким образом, форма дифференциала сохранилась (т.е осталась инвариантной): дифференциал функции имеет один и тот же вид : произведение производной функции по какой-либо переменной на дифференциал этой переменной не зависимо от того является ли эта переменная функции или независимой переменной, т.е аргументом. Опишите способы нахождения производной степенно-показательной функции. Объясните логарифмическое дифференцирование и проиллюстрируйте его на примере. y=uv Чтобы найти производную степенно-показательной функции достаточно продифференцировать ее как показательную, а затем как степенную и полученный результат сложить. y’= uv*ln u*v’+v uv-1*u’ Логарифмическое дифференцирование: на примере y=xsin(x+1) Логарифмируем обе части. ln y=sin(x+1)*ln x Дифференцируем обе части, считая, что y’=y(x). 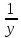 *y’=cos(x+1)*ln x+sin(x+1)* *y’=cos(x+1)*ln x+sin(x+1)*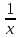 Выражаем у’. y’= xsin(x+1)( cos(x+1)*ln x+ 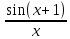 ) )
Пусть функция f(x), определена на интервале (а,b) имеет в каждой точке x∈(а,b) производную f”(x) и пусть x0∈(а,b). Если при x=x0 у производной f ’(x) существует производная, то она называется второй производной функции f(x) или производной второго порядка. Производную от второй производной называют производной третьего порядка. Аналогично определяется производная y(n) любого порядка, n=1,2,3…,если существет производная y(n-1) . Производной нулевого порядка считается сама функция. Производной n-ого порядка f(n)(x0)= 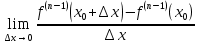 Теорема. Пусть у1=f1(x) и у2=f2(x) имеют производные n-ого порядка, тогда функция у1+у2= f1(x)+f2(x), а функция у1*у2= f1(x)*f2(x) также имеют производные n-ого порядка в т x0 и они равны: (у1+у2)(n)= у1(n)+ у2(n) (у1*у2)(n)= у1(n) у2+n у1(n-1) у2(1) 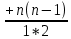 у1(n-2) у2(2) у1(n-2) у2(2)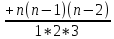 у1(n-3) у2(3)+…+ у1у2(n)-Формула Лейбница у1(n-3) у2(3)+…+ у1у2(n)-Формула Лейбница
Значение дифференциала d(dy), то есть дифференциала от первого дифференциала, в некоторой точке х0 называется вторым дифференциалом функции f в этой точке и обозначается через d 2y (читается: d два у), то есть d 2y = f "(x0)dx2. d ny = d(d n-1y) или dny = yndxn,n = 1,2,... Док-во (методом математической индукции) : Для n=1, n=2-доказано d(dy)= d 2y. Пусть верно для n-1 т.е. dn-1y = yn-1dxn-1. d(dn-1y )= d(yn-1dxn-1)= yndxn таким образом d(dn-1y )= yndxn Свойства дифференциалов высших порядков dn(y1+y2)=dny1+dny2 dn(cy) = cdny, с —постоянная. Dn(y1y2) = (dy1 + dy2){n} (это означает, что данная формула записывается по аналогии с биномиальной формулой). (a+b)n=an+nan-1b+ 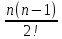 an-2b2+…+ bn an-2b2+…+ bn |
