Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения
 Скачать 4.57 Mb. Скачать 4.57 Mb.
|
4.3. Синтез алгоритмов выдерживания ограничений в рамках диапазона высот и скоростей полетаВ первом разделе было показано, что с точки зрения безопасности полетов наиболее опасен выход на рассматриваемое пространство состояний не является метрическим; одна из координат подлежащих ограничению, в частности скорость является "управлением" (входит в правую часть уравнения высоты) для другой. Первая трудность может быть устранена нормированием пространства. Вторая же вносит неоднозначность в выбор параметров управления ограничения. Произведем вывод основных зависимостей алгоритма ограничения с учетом изложенных особенностей. Пусть движение летательного аппарата описывается следующей системой дифференциальных уравнений 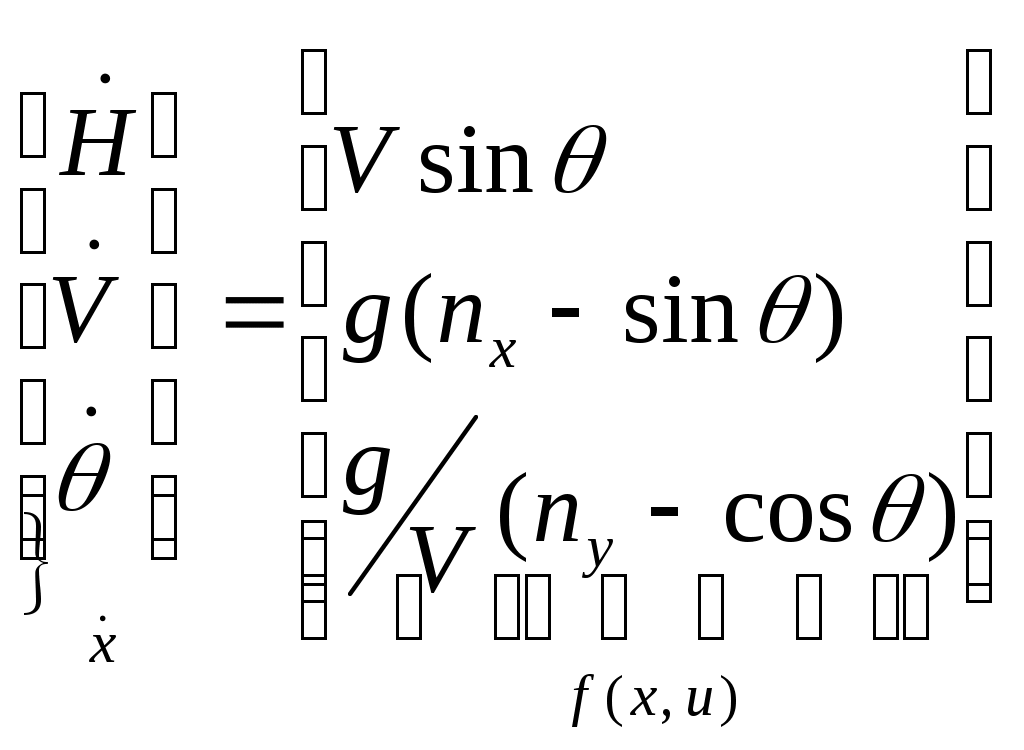 . (4.36) . (4.36)Границу ограничения (см. рис.4.13) зададим в срезе пространства Х для относительных координат 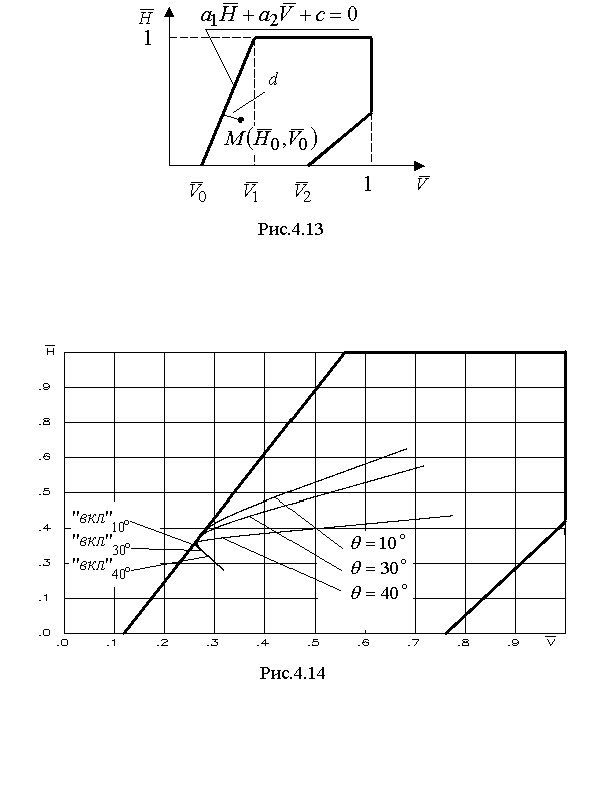 Рис.4.13 Рассмотрим случай приближения точки где в соответствии с рис.4.13: Как было изложено ранее, расстояние до границы диапазона (4.37) определится в виде В (4.38) 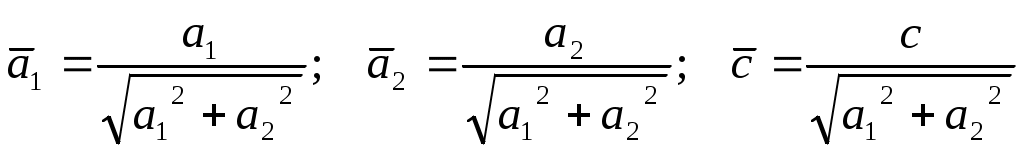 . .Возьмем почленно первую и вторую производные по времени t от расстояния d и проанализируем полученные выражения. Итак, с учетом того, что для составляющей изменения расстояния по высоте имеем Соответственно, первая и вторая производная от составляющей по скорости равны Анализ полученных выражений, и в частности, (4.40), (4.42) показывает, что общим управлением, влияющим на ускорение торможения Таким образом, для объекта, описанного расширенной системой уравнений (4.36), управление ограничения будет задано вектором Тогда расстояние до границы ограничения, при котором необходимо включить в работу алгоритм ограничения, и компенсационное управление определится следующими выражениями 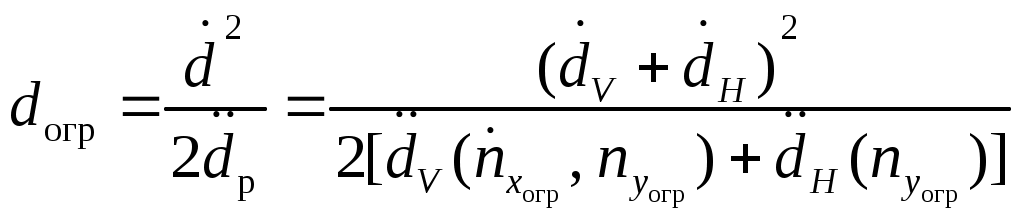 ; (4.44) ; (4.44)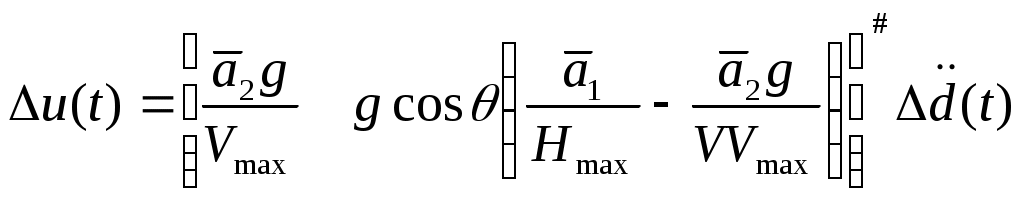 . (4.45) . (4.45)На рис.4.14 приведены результаты моделирования процесса ограничения в рамках диапазона высот и скоростей полета при выходе самолета на левую границу диапазона, описанную выражением (4.38).  Рис.4.14 Исходный режим полета: H=2км, V=1300км/ч. Исследовался набор высоты с различными углами наклона траектории и потерей скорости. Налицо адаптивные свойства алгоритма к начальным условиям. Так увеличение угла наклона траектории приводит к более раннему срабатыванию алгоритма ограничения. |
