Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения

• Название: Адаптивность к свойствам объекта, форме поверхности ограничения
• Анкор: Системы ограничения
• Дата: 28.03.2022
• Размер: 4.57 Mb.
• Имя файла: Текст монографии.doc
• Тип: Анализ; #422574
• страница: 16 из 22

4.2.2. Увод самолета в горизонтальной плоскости

Пусть движение самолета в горизонтальной плоскости описывается системой уравнений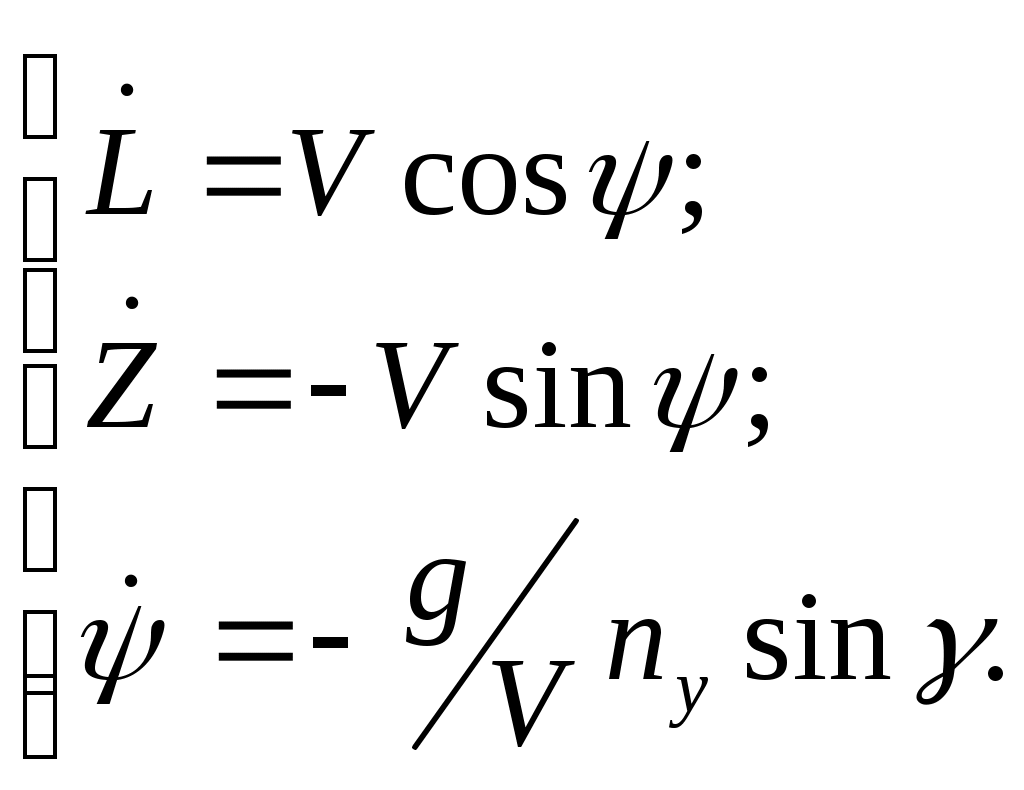

(4.29)

Ограничение в координатах OLZ представлено линией (см. рис.4.9)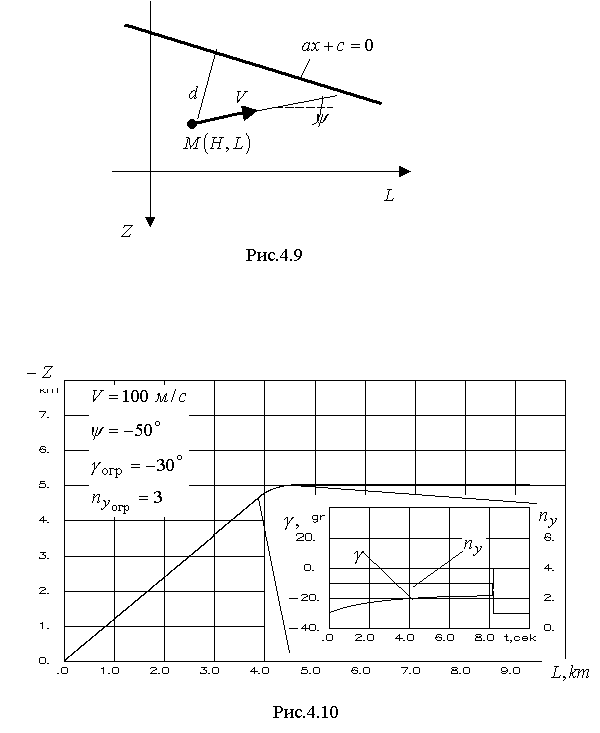

. (4.30)



Рис.4.9

Нетрудно заметить, что выражение (4.30) является развернутым представлением уравнения (4.12) при условии, что .

Схема постановки данной задачи представлена на рис.4.9.

Для синтеза алгоритмов ограничения воспользуемся подходом, изложенным в параграфе 4.1. В соответствии с ним, представим систему уравнений (4.29) в виде (4.2), обозначив вектор состояния , вектор псевдоуправления , вектор управления . Задавшись управлением ограничения и формально используя выражения (4.6 – 4.9) после несложных преобразований получим

• 
  кратчайшее расстояние от самолета до линии ограничения
  

, (4.31)

где .

• 
  скорость приближения самолета к ограничению
  

; (4.32)

• 
  располагаемое ускорение торможения самолета при условии срабатывания системы ограничения
  

; (4.33)

• 
  коррекция управления на этапе ограничения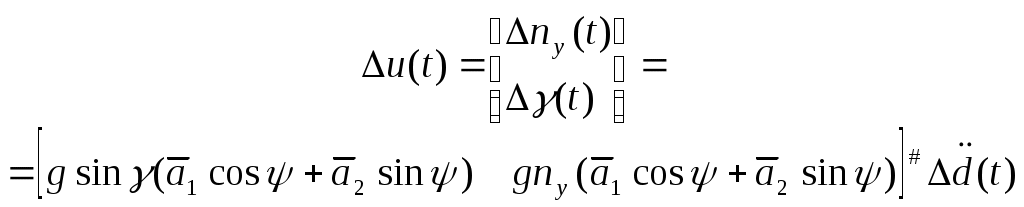
  

. (4.34)

В итоге можно записать выражение для дальности срабатывания системы ограничения в виде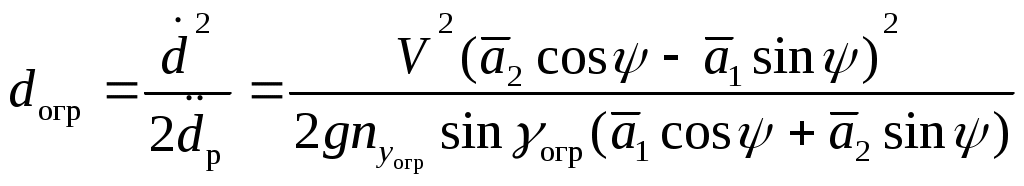

. (4.35)

Необходимо отметить следующий очевидный факт, касающийся задания управления ограничения. Для того, что бы самолет выполнял маневр увода строго в горизонтальной плоскости перегрузка увода и крен должны быть связаны зависимостью

.

Если же на перемещение самолета в вертикальной плоскости при выполнении увода в "горизонте" специальных условий не накладывается, то и могут быть заданы из неких других соображений.

Анализ (4.35) показывает, что дальность срабатывания растет с увеличением скорости полета и тем меньше, чем больше заданное управление ограничения. Результаты моделирования процесса увода в горизонтальной плоскости по приведенному алгоритму представлены на рис.4.10 – 4.12. Линия ограничения при моделировании задавалась следующими параметрами

.

На рис.4.10 выносками показан переходный процесс изменения угла крена и нормальной перегрузки на участке увода. Из него видно, что в первоначальный момент времени алгоритм реализует заданное управление ограничения. Далее, для поддержания при изменении курсового угла ψ, производится сброс управления с незначительной коррекцией управления .



Рис.4.10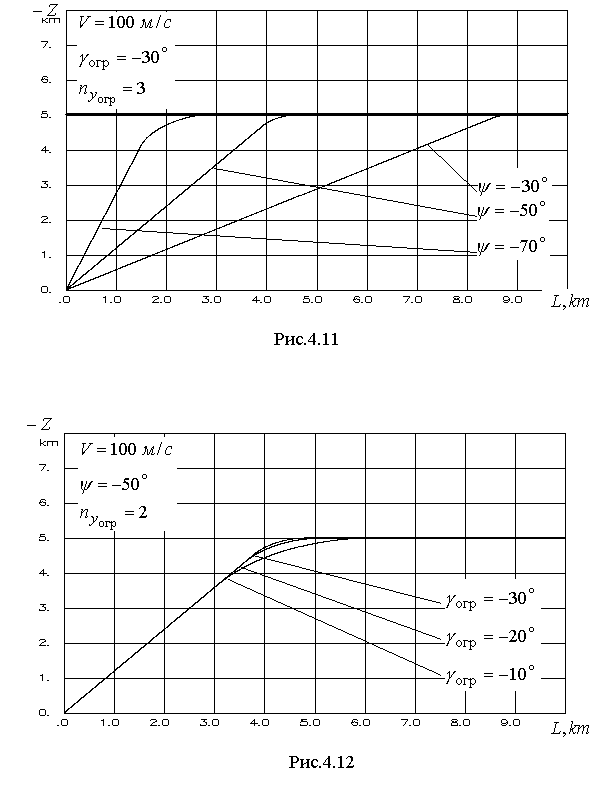



Рис.4.11



Рис.4.12

На рисунках 411 и 4.12 иллюстрируются свойства адаптивности алгоритма к изменению углов подхода самолета к линии ограничения, а также к настройкам управления ограничения при постоянном значении .