Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения

• Название: Адаптивность к свойствам объекта, форме поверхности ограничения
• Анкор: Системы ограничения
• Дата: 28.03.2022
• Размер: 4.57 Mb.
• Имя файла: Текст монографии.doc
• Тип: Анализ; #422574
• страница: 19 из 22

5.2. Алгоритмы расчета углов положения самолета в пространстве при уводе его от препятствия

Очевидно, что угловое положение самолета в пространстве при уводе лежит в прямой зависимости от ориентации плоскостей U и K, определяемых, в частности, углами ζ и η (см. рис.5.2), которые в свою очередь зависят от вида поверхности ограничения и положения точки Т на ней.

Координаты точки Т определяются путем совместного решения уравнений поверхности (5.1) и линии, содержащей вектор скорости самолета. Каноническое представление последней имеет вид

. (5.2)

Здесь - проекции вектора скорости на оси рассматриваемой системы координат.

Тогда плоскость, касательная к поверхности ограничения в точке Т, может быть представлена уравнением

, (5.3)

где , , – значения частных производных поверхности ограничения в точке Т(X,Y,Z) по соответствующим параметрам.

В случае рассмотрения в качестве поверхности ограничения вогнутой поверхности (здесь под вогнутой поверхностью понимается поверхность, все точки которой относительно точки Т касательной поверхности в некоторой заданной окрестности находятся на меньшем расстоянии от ЛА, чем точка Т). Из физических соображений, плоскость К необходимо строить используя информацию о координатах трех близлежащих к ЛА точек на поверхности ограничения. Данные точки могут быть получены с помощью бортовых средств самолета. Тогда уравнение плоскости К будет иметь вид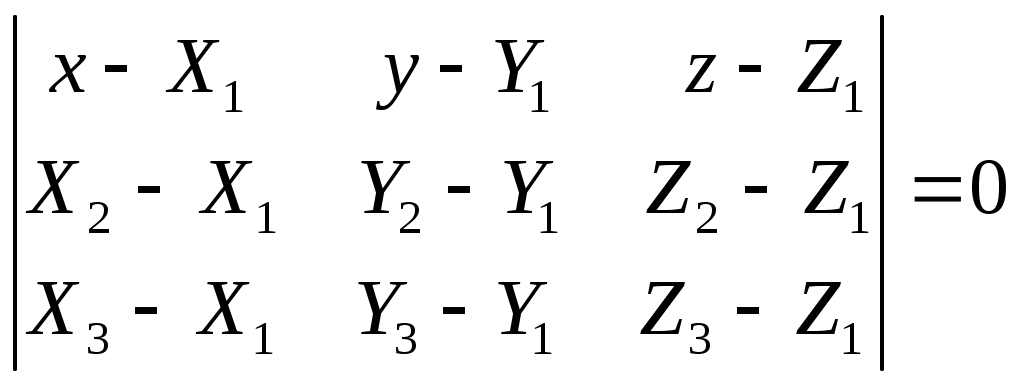

(5.4)

Для удобства дальнейших преобразований запишем уравнения (5.3) и (5.4) в виде

, (5.5)

где для уравнения (5.3)

, , ,

а в случае использования уравнения (5.4)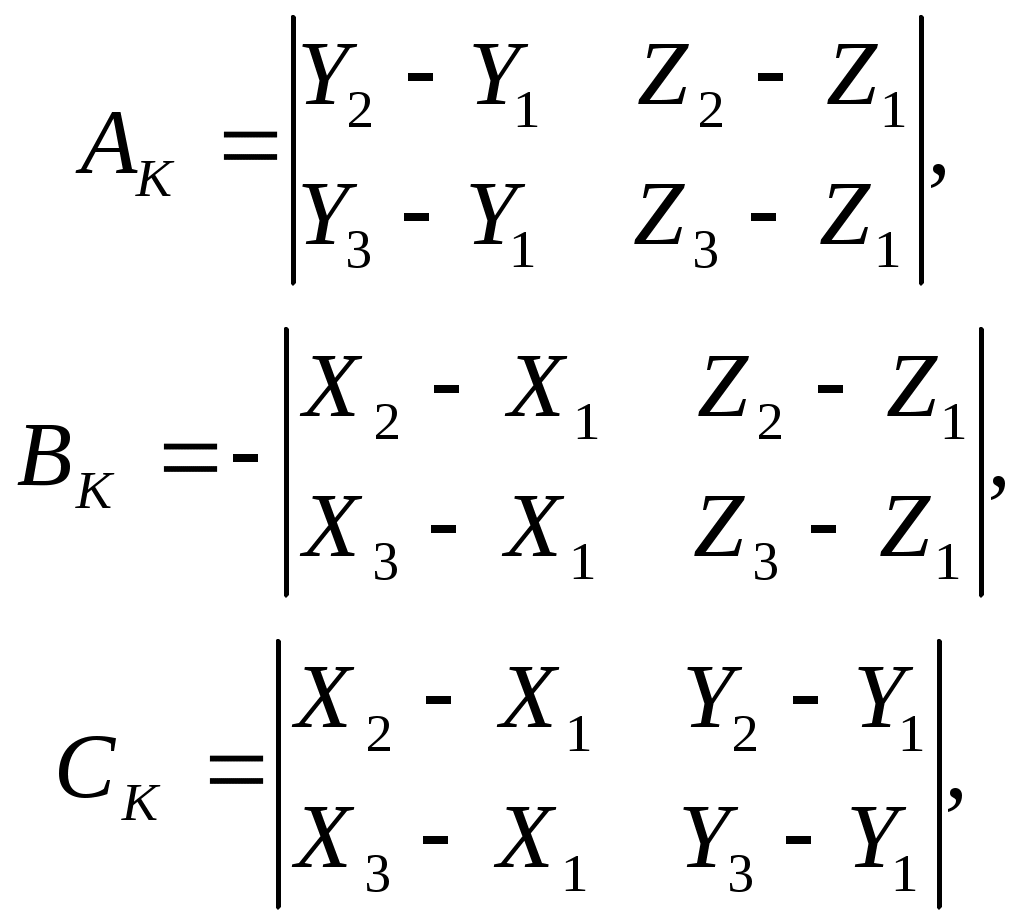



и для обоих случаев

.

При ориентации плоскости U в пространстве учитывается, что скорость увода самолета от препятствия должна иметь максимальное значение. Это может быть достигнуто в случае, когда плоскость U содержит нормаль к плоскости К в точке Т и точку с текущими координатами ЛА . Тогда параметры уравнения

, (5.5)

описывающие положение плоскости U, рассчитываются по зависимостям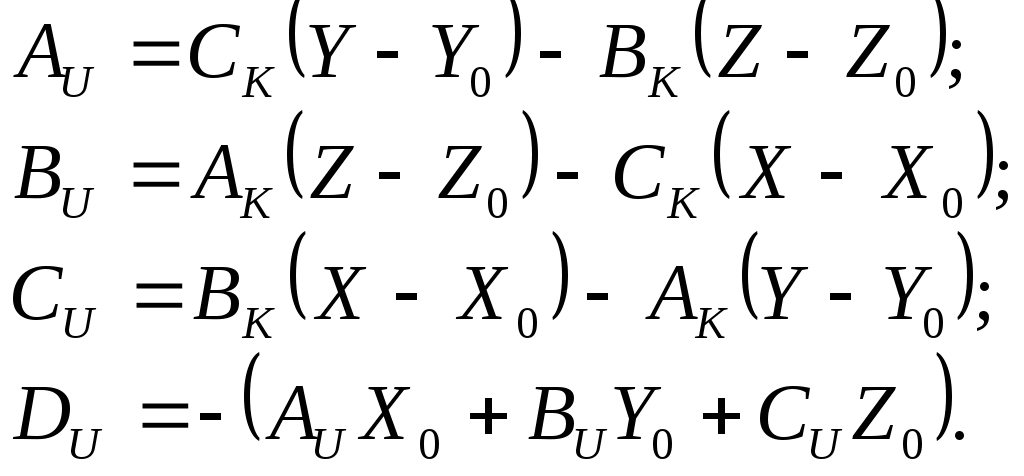



При этом угол ζ между плоскостью увода U и вертикальной плоскостью В (см. рис.5.2) равен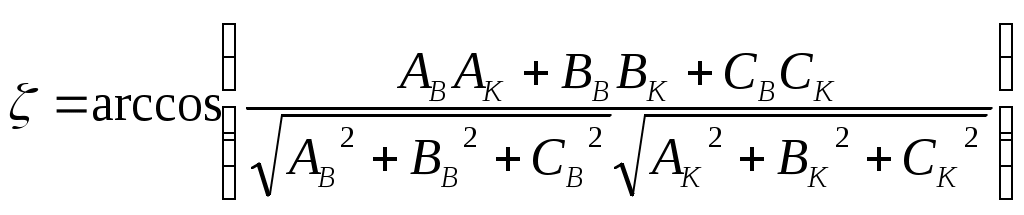

, (5.6)

где – коэффициенты, характеризующие ориентацию плоскости B в пространстве.

Учитывая, что по определению 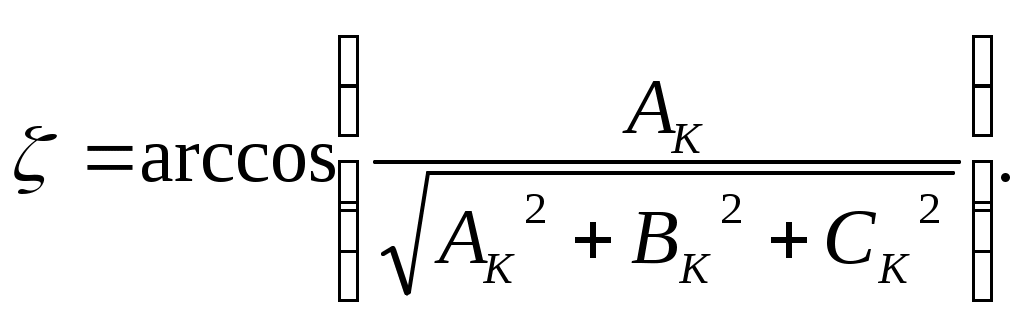, выражение (5.6) запишется в виде

(5.7)

Для того чтобы самолет не входил в спираль и удерживался в плоскости U, силы, перпендикулярные к этой плоскости (см. рис.5.3), должны быть уравновешены.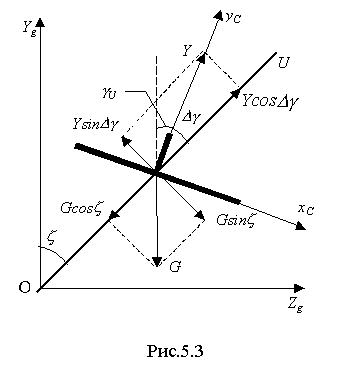



Рис.5.3

Это обеспечивается разворотом самолета на угол откренивания [40]

(5.8)

В итоге, необходимый крен самолета будет равен

. (5.9)

Угол наклона траектории самолета при уводе представляет собой угол (см. рис.5.2) между прямой S и плоскостью G, т.е. .

Так как прямая S образуется пересечением плоскостей U и К, и проходит через точку Т, то согласно [25] ее каноническое представление имеет вид

, (5.10)

где определяются соотношениями:



В результате, значение 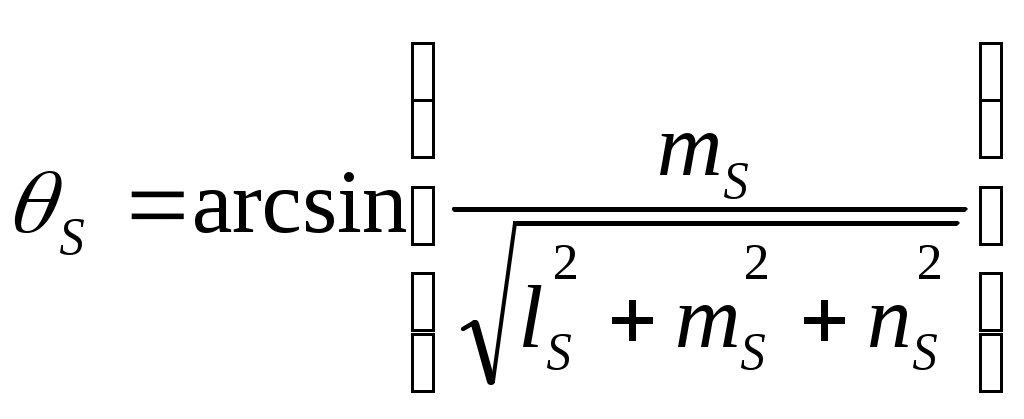рассчитывается как угол между прямой и плоскостью по формуле

. (5.11)

В итоге получены выражения для определения и текущего перерасчета заданных углов положения самолета в пространстве в процессе выполнения маневра уклонения от поверхности ограничения.