Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения
 Скачать 4.57 Mb. Скачать 4.57 Mb.
|
4.1.3. Вывод расчетных зависимостей алгоритмаограниченияПо аналогии вывода расчетных зависимостей (2.45 – 2.48) алгоритма выдерживания ограничений на параметры вектора состояния детерминированной непрерывной управляемой многоуровневой динамической системы для рассматриваемого случая имеем кратчайшее расстояние от самолета до плоскости ограничения скорость приближения самолета к поверхности ограничения (первая производная от расстояния) располагаемое ускорение торможения самолета при условии срабатывания системы ограничения коррекция управления на этапе ограничения В (4.8 – 4.9) матрицы 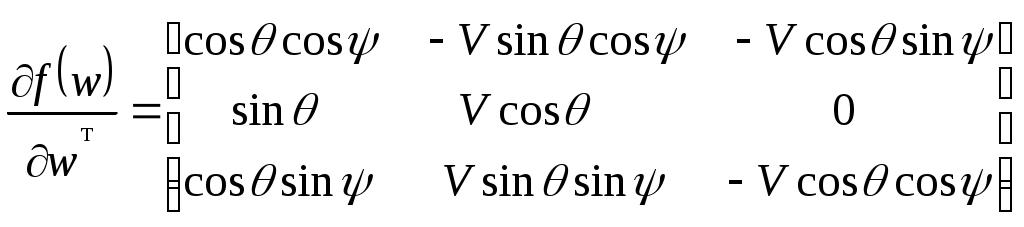 ; (4.10) ; (4.10)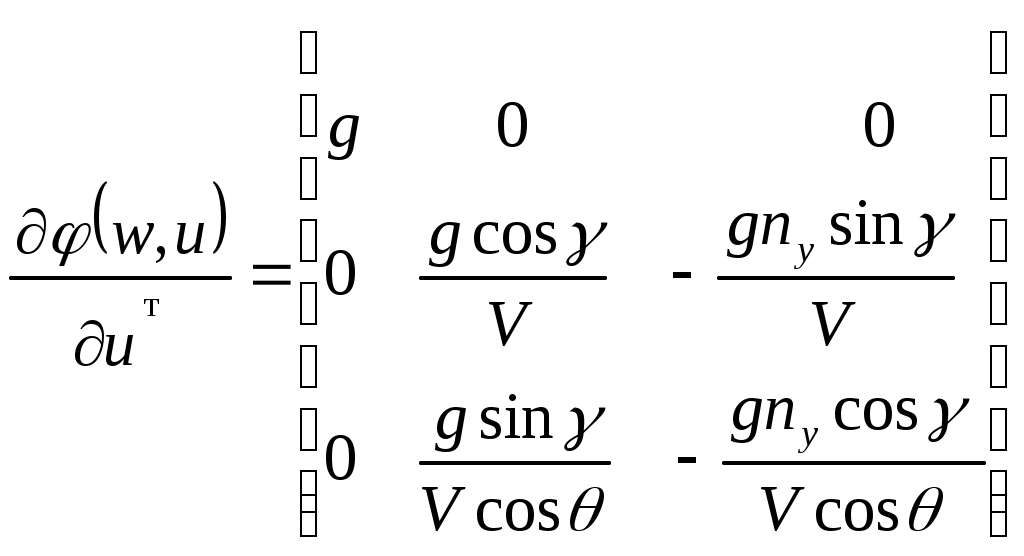 . (4.11) . (4.11)На рис.4.3 представлена траектория увода самолета от поверхности ограничения в виде параболоида вращения. 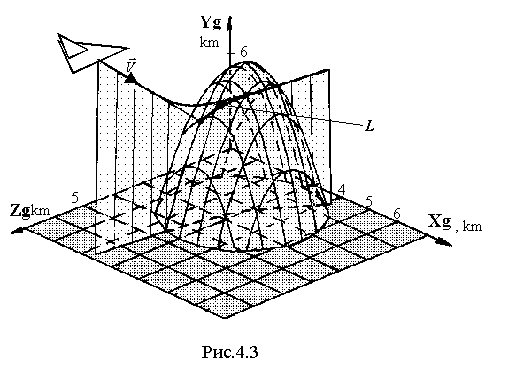 Рис.4.3 Алгоритм ограничения включается в работу при наступлении условия При включении в работу алгоритма ограничения, под действием управления Схожая задача с аналогичными результатами решалась авторами монографии [2]. Однако применяемый ими метод прямой оптимизации в вычислительном плане существенно сложнее. Кроме того, он исключает из процесса формирования траектории полета летчика. Последнее неприемлемо при решении задач, направленных на обеспечение безопасности полета с летчиком в контуре управления ЛА. 4.2. Частные задачи ограничения траекторныхпараметров движения в вертикальной игоризонтальной плоскости4.2.1. Увод самолета в вертикальной плоскостиРассмотрим задачу синтеза алгоритмов увода самолета в вертикальной плоскости от поверхности ограничения заданной наклонной линией с уравнением Графическая интерпретация задачи в координатах H, L представлена на рис.4.4.  Рис.4.4 Для описания движения центра масс самолета воспользуемся моделью (4.2) и методически исследуем два случая. Пусть в первом случае самолет снижается с постоянной скоростью, во втором случае 1. Увод самолета с Для данного случая система (4.2) будет иметь следующие составляющие. Вектор состояния 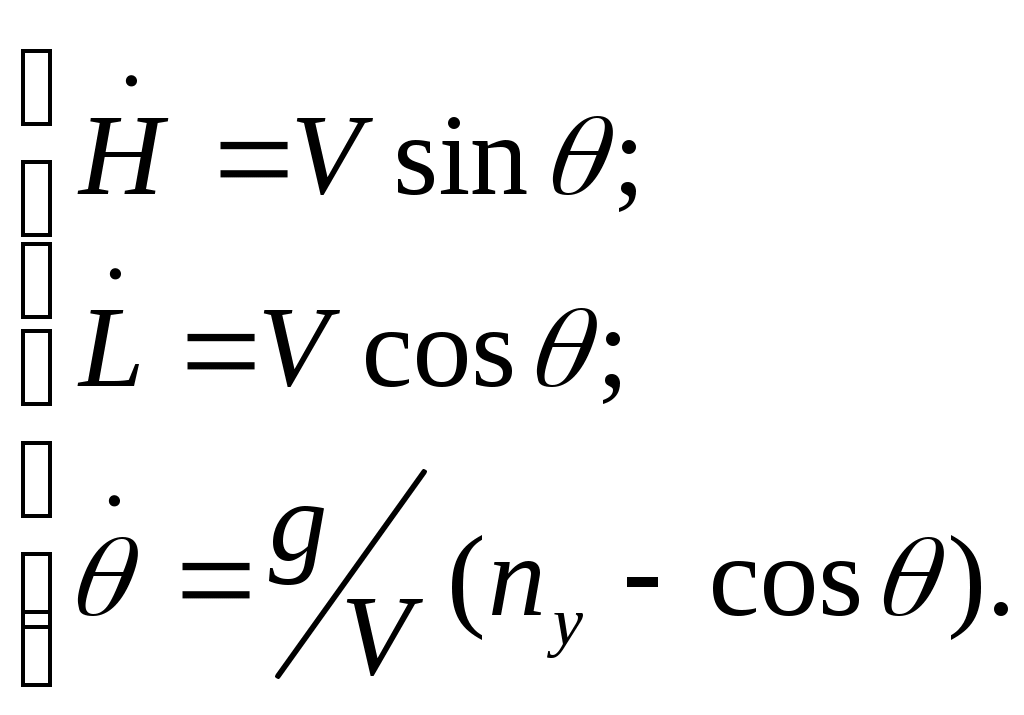 (4.13) (4.13)Задавшись управлением ограничения дальность до препятствия первая производная от дальности располагаемое ускорение торможения самолета при условии срабатывания системы ограничения коррекция управления на этапе ограничения В соответствии с методом выдерживания ограничений активизация алгоритма ограничения происходит в случае сближения самолета с препятствием на величину где дальность срабатывания системы ограничения с заданным управлением 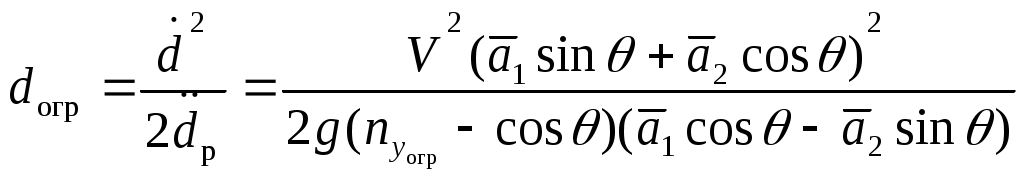 . (4.19) . (4.19)Анализ (4.19) показывает существенную зависимость дальности срабатывания 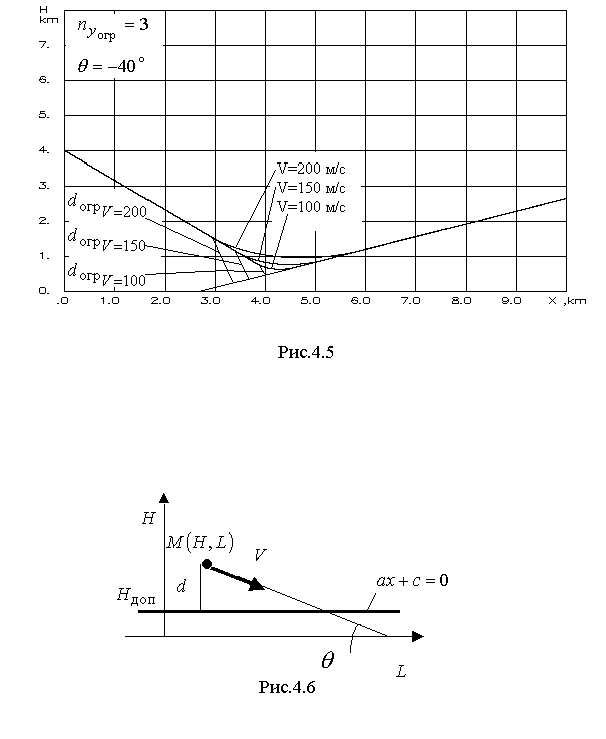 Рис.4.5 Кроме того, очевидно влияние на дальность срабатывания алгоритма соотношение углов наклона траектории самолета и линии ограничения. Положение в пространстве последней характеризует матрица строка где µ - полярный угол линии Чтобы показать такую зависимость рассмотрим задачу увода самолета от горизонтальной линии ограничения. Схема постановки задачи изображена на рис.4.6. В этом случае движение центра масс самолета можно описать системой уравнений второго порядка 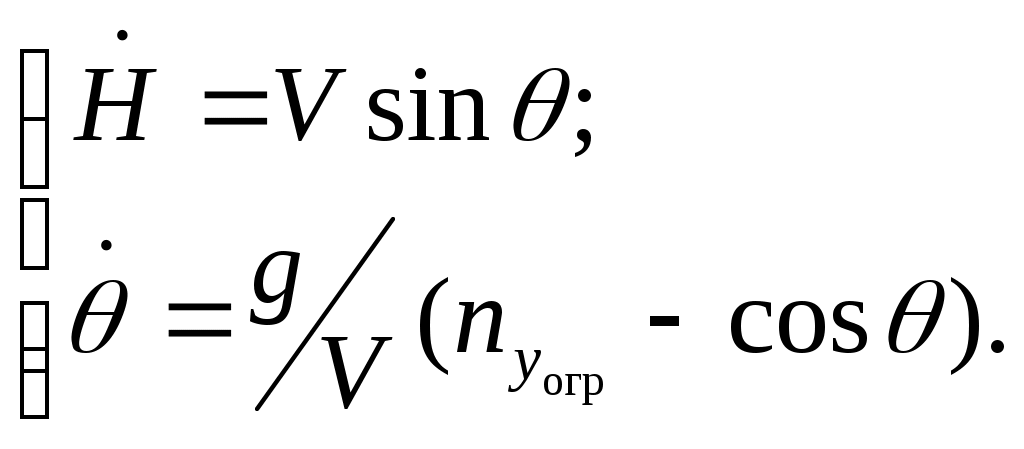 (4.20) (4.20)А уравнение линии ограничения сведется к виду  Рис.4.6 Выражение (4.21) можно легко получить из (4.12) положив Подставив значения коэффициентов матрицы-строки a в (4.19) и (4.17), получим соотношения для дальности включения алгоритма и коррекцию управления на этапе ограничения Анализ зависимости (4.23) показывает, что чем больше начальный угол наклона траектории, тем раньше вступит в работу система ограничения. В пределе при Другую картину дает учет управления 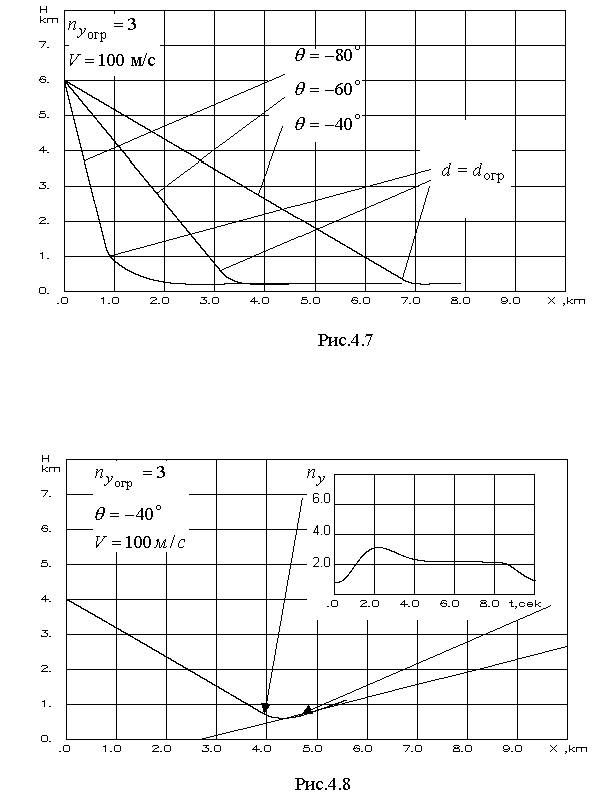 Рис.4.7 2. Увод самолета с опасной высоты в вертикальной плоскости с Данному случаю соответствует система уравнений 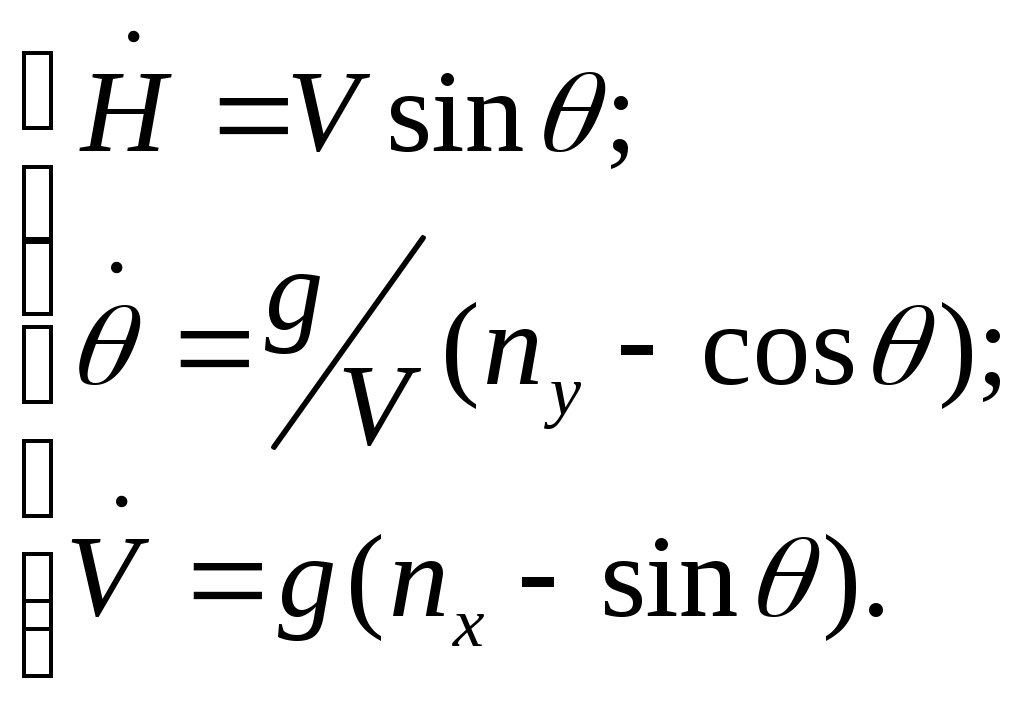 (4.25) (4.25)Представим систему (4.25) в виде (4.2), при этом и воспользовавшись изложенной методикой синтеза алгоритмов выдерживания ограничений, имеем дальность срабатывания системы ограничения (в данном случае соответствует высоте срабатывания) коррекция управления на этапе ограничения 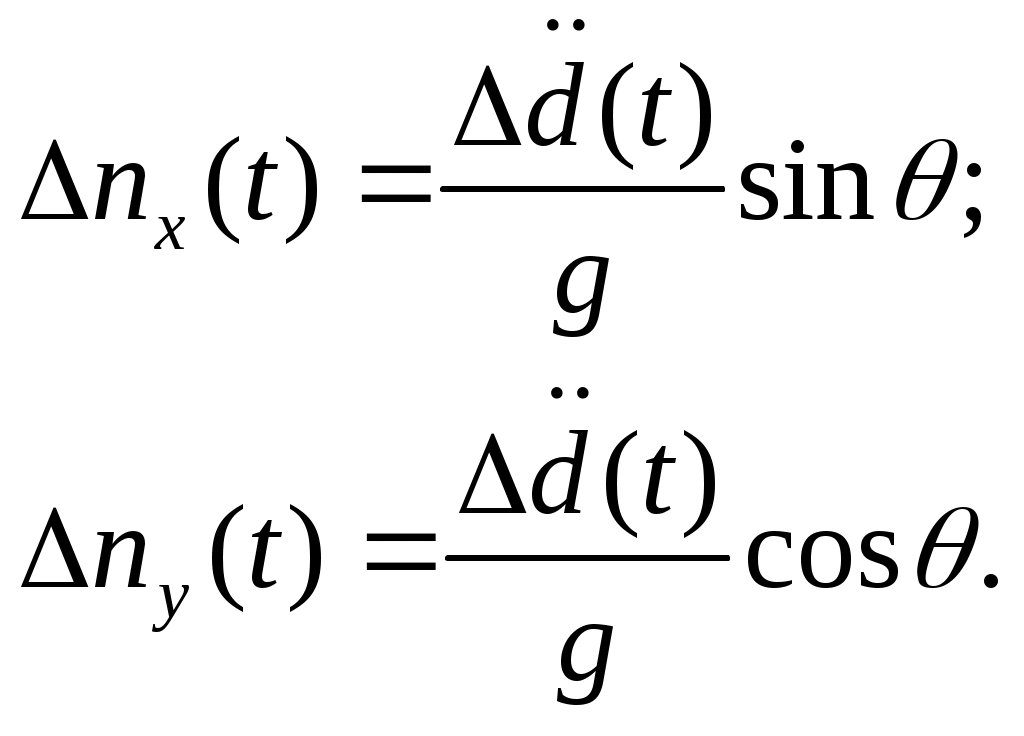 (4.28) (4.28)Как видно из полученных выражений Следует отметить, что приведенные здесь алгоритмы выдерживания ограничений работоспособны и при исследовании движения летательного аппарата как твердого тела. Так, на рис.4.8 представлены результаты моделирования увода самолета в вертикальной плоскости от наклонной линии. Аэродинамические, геометрические и массовые характеристики при этом соответствуют характеристикам легкого маневренного истребителя. Также при моделировании учитывались реальные характеристики рулевых приводов. Выноской приведен переходный процесс изменения нормальной перегрузки на участке увода. Из полученных результатов видно отсутствие ошибки выдерживания заданного ограничения.  Рис.4.8 Таким образом, анализ полученных выражений и результатов показывает очевидность адаптационных свойств алгоритма ограничения к начальным условиям пикирования самолета, что выгодно отличает предлагаемые алгоритмы от используемых на практике. |
