Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения

• Название: Адаптивность к свойствам объекта, форме поверхности ограничения
• Анкор: Системы ограничения
• Дата: 28.03.2022
• Размер: 4.57 Mb.
• Имя файла: Текст монографии.doc
• Тип: Анализ; #422574
• страница: 11 из 22

3.2. Особенности выдерживания ограничений

на наблюдаемые параметры движения

маневренного самолета

Необходимо отметить, что большой спектр практических задач по исследованию динамических систем базируется на измерении компонент, не входящих в вектор состояния посредством комплекса датчиков.

В данном параграфе рассматриваются особенности метода выдерживания ограничений на компоненты вектора наблюдений динамической системы на примере ограничения нормальной перегрузки маневренного самолета. При этом для упрощения задачи сделано допущение о полнокомпонентном, мгновенном измерении интересующих параметров.

Пусть движение объекта управления описывается дифференциальным уравнением вида

, (3.12)

а вектор наблюдений представлен выражением

, (3.13)

где y – n-мерный вектор выхода, определенный в пространстве , С – матрица постоянных коэффициентов соответствующей размерности.

Запишем уравнения (3.12) и (3.13) в форме "вход-выход". Для этого выразим вектор х из (3.13) и подставим полученное выражение в (3.12). После выполнения соответствующих преобразований окончательно имеем

. (3.14)

Отметим, что в (3.14) и далее в случае наличия особенностей матрицы С знак обращения матрицы следует заменить на знак псевдообращения.

Зададим в пространстве граничную гиперплоскость уравнением

, (3.15)

где а –матрица строка соответствующей размерности, с – скаляр,и получим для динамической системы, представленной математической моделью (3.14), основные соотношения алгоритма управления (2.20) адаптивной системы выдерживания ограничений на компоненты вектора у. При этом будем считать, что пространство предварительно отнормированно.

Итак, в соответствии с изложенной методикой взвешенное расстояние до границы (3.15) определяется уравнением

. (3.16)

Дифференцирование выражения (3.16) по времени позволяет получить следующие зависимости

; (3.17)

. (3.18)

Обеспечение на этапе ограничения осуществляется корректировкой управления ограничения на величину

(3.19)

или с учетом соответствующих преобразований

(3.20)

В (3.20) - вектор наблюдений в момент срабатывания системы ограничения. С точки зрения вычислительных трудностей, форма записи (3.19) более удобна, так как под знаком псевдообращения находится матрица строка и вследствие этого, данная процедура разрешается аналитически.

Применим изложенный здесь подход к задаче ограничения нормальной перегрузки.

Пусть движение самолета описывается системой линейных дифференциальных уравнений второго порядка

. (3.21)

В качестве наблюдаемых параметров будем рассматривать нормальную перегрузку и угловую скорость . В этом случае выражение (3.13) перепишется как

. (3.22)

Т
огда, задавшись в пространстве Y ограничением в виде, показанном на рис.3.6 (то есть, задав параметры линии ограничения (3.15) в виде: а=[-1 0], с= ), получим развернутые выражения (3.16) – (3.19).

Итак,

; (3.23)

; (3.24)

; (3.25)

. (3.26)

Уравнения (3.23) – (3.26) являются основными зависимостями алгоритма функционирования адаптивной системы ограничения нормальной перегрузки при использовании доступной информации о параметрах движения самолета. На рис.3.7 представлены переходные процессы выхода самолета на перегрузку в условиях ограничений, как в идеальных условиях, так и при учете датчиков полетной информации.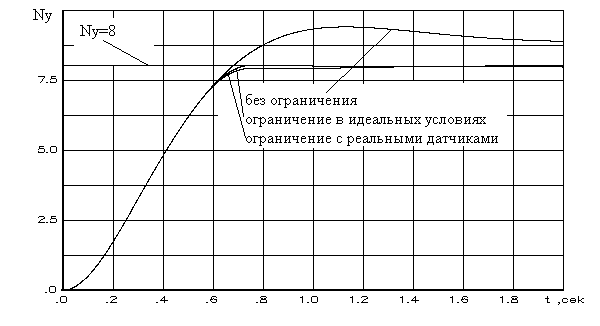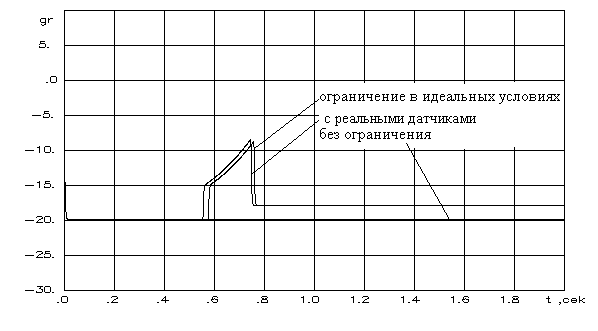



Рис.3.7

В работе использовалась модель датчиков в виде динамической системы второго порядка с генераторами погрешностей в виде [35]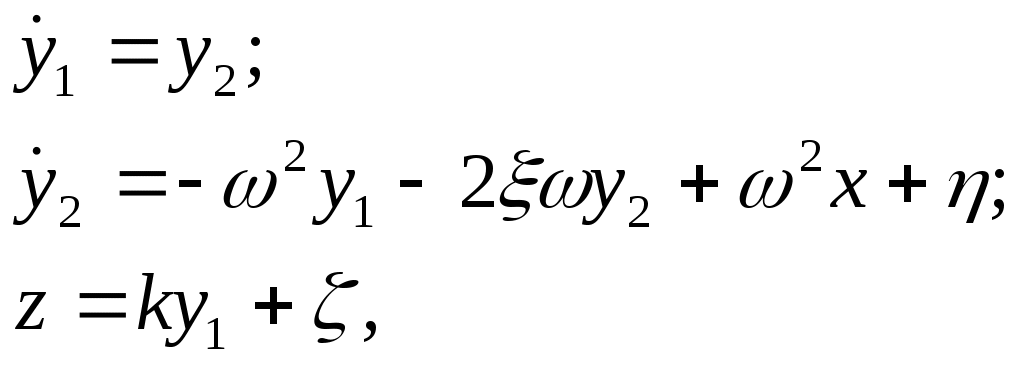

(3.27)

где - вспомогательные переменные; х – полезный, измеряемый сигнал; – частота собственных недепфированных колебаний измерительного элемента датчика; - относительный коэффициент затухания колебаний измерительного элемента датчика; – помехи на входе датчика; k – коэффициент передачи датчика; – ошибки датчика, возникающие при съеме сигнала.

Как видно из результатов моделирования алгоритм ограничения нормальной перегрузки робастен к погрешностям реальных датчиков.

На рис.3.8 приведены результаты оценки влияния постоянной времени рулевого привода на точность выдерживания ограничения . При этом динамические свойства рулевого привода описывались дифференциальным уравнением вида

, (3.28)

где Т_рп – постоянная времени рулевого привода; k_ус – коэффициент усиления; Δу, - соответственно, положение и скорость выходного штока рулевого привода; Δz – перемещение золотника рулевого привода.

Использование в проведенных исследованиях выражения (3.28) явилось следствием допущения о том, что влияние сжимаемости рабочей жидкости рулевого привода и инерционности нагрузки мало. Это возможно при небольших габаритах и массе рулевого привода, что и имеет место на современных самолетах.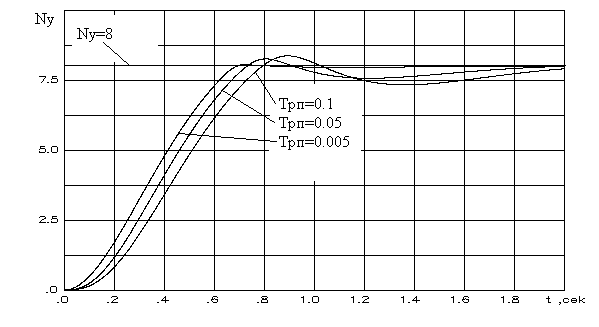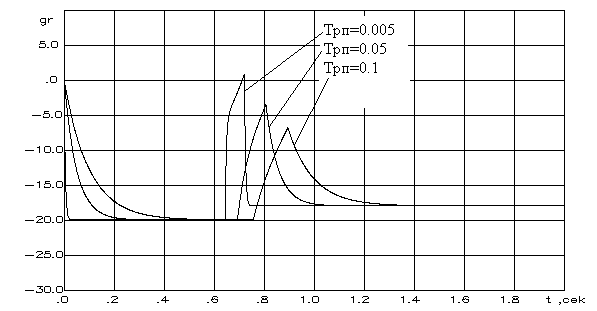



Рис.3.8

Анализ полученных результатов показывает, что точность выдерживания ограничения естественно зависит от быстродействия рулевого привода. Однако моделирование процесса ограничения при реальных характеристиках рулевого привода (Трп=0.05) дает приемлемую точность выхода самолета на . Ошибка составляет примерно 0.3 ед. перегрузки, что соответствует 4% от допустимого значения. Таким образом, можно сделать вывод о робастности алгоритмов ограничения и к реальным характеристикам рулевых приводов.