Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения
 Скачать 4.57 Mb.
|
3.4. Ограничение в пространстве двух компонентвектора состояния (на примере задачи ограниченияуглов атаки и скольжения маневренного самолета)В предыдущих параграфах рассмотрены задачи ограничения одной из компонент вектора состояния летательного аппарата, а также величин вычисляемых на их основе. В этом параграфе рассматривается задача выдерживания двумерных, связанных между собой ограничений. Рассмотрим модельную задачу выдерживания границ эксплуатационной области в сечении  для с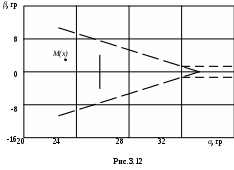амолета, движение которого описывается системой линейных дифференциальных уравнений пятого порядка , (3.34)где  ;  .Г  раницу эксплуатационной области зададим сечением пространства Х в координатах в виде, изображенном на рис.3.12 штриховой линией.Сплошная линия характеризует стандартную настройку для однопараметрической системы ограничения угла атаки. Получим расчетные зависимости алгоритма выдерживания ограничения для границы, заданной уравнением  (3.35)и обусловленной положительными значениями угла скольжения β. В соответствии с приведенным рисунком, параметры уравнения линии ограничения (3.35) заданы в виде  .Тогда кратчайшее расстояние от произвольной точки М(х), характеризующей состояние объекта ограничения в пространстве Х до границы (3.35) определится как  , (3.36)где  . В соответствии с изложенной методикой, для данного описания движения самолета системой (3.34) применимы уравнения синтеза системы выдерживания ограничений рассмотренные применительно к детерминированной линейной непрерывной динамической системе в стационарном случае. А именно 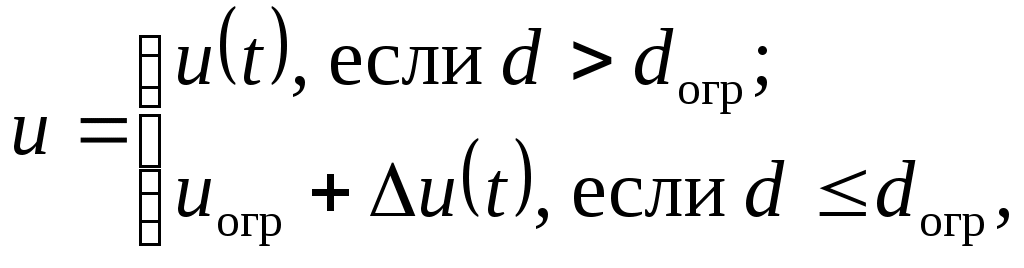 где  ;  ;  ;  .Задавшись управлением ограничения в виде  , (3.37)где  - заданное располагаемое отклонение стабилизатора на пикирование;  - заданное располагаемое отклонение руля направления на уменьшение скольжения, можно записать развернутые выражения компонент алгоритма ограничениярасстояние до границы ограничения  ; (3.38)первая производная от расстояния  ; (3.39)располагаемое ускорение торможения 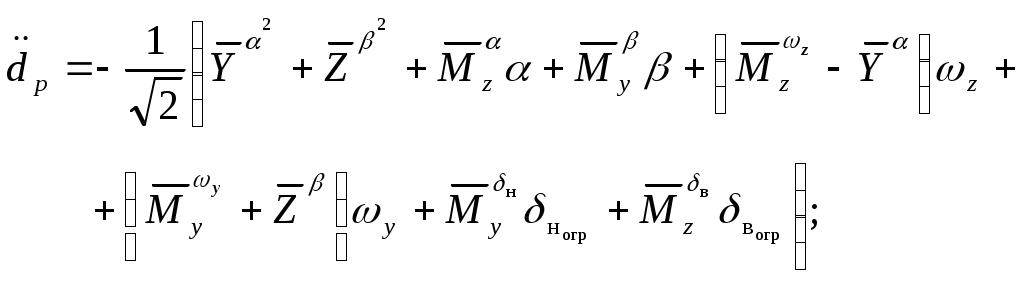 (3.40)коррекция управления на этапе ограничения 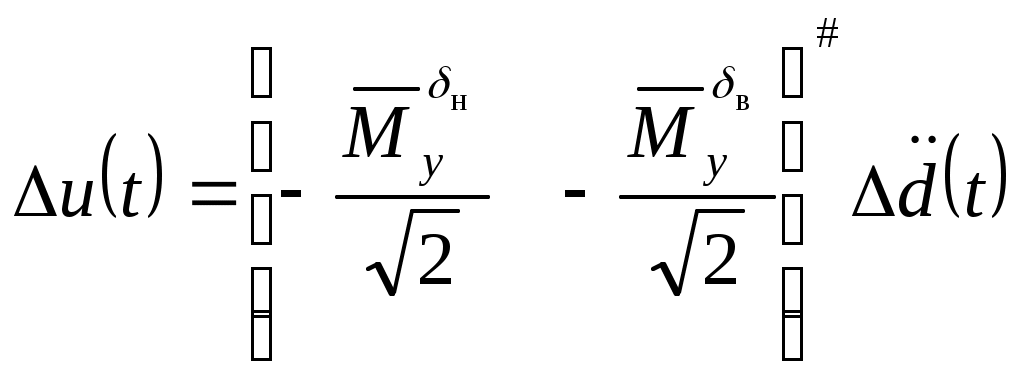 . (3.41)Работа алгоритма выдерживания ограничения в координатах иллюстрируется на рис.3.13 – 3.14.При моделировании задача ограничения формулировалась следующим образом – обеспечить непротыкание линии ограничения в координатах 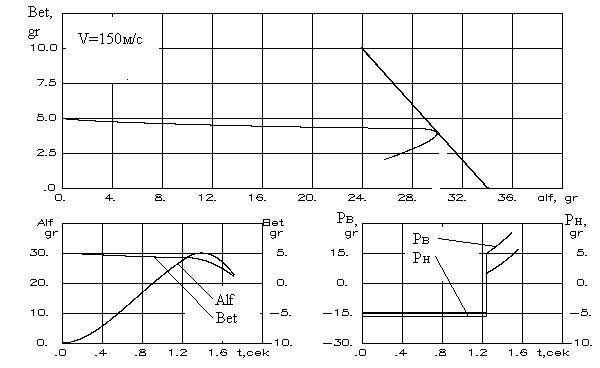. Задача балансировки объекта на уровне допустимых значений параметров – не рассматривалась. Рис.3.13 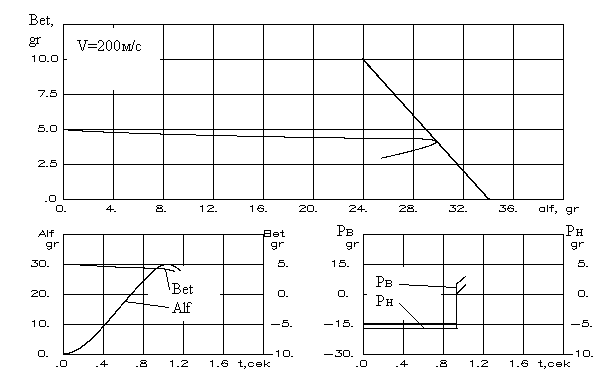 Рис.3.14 Анализ результатов моделирования показывает высокую эффективность выдерживания ограничения. Кроме того, можно сделать вывод об адаптивности метода к режимам полета. Так, снижение скорости полета самолета лишь изменяет момент времени включения алгоритма ограничения. |