Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения

• Название: Адаптивность к свойствам объекта, форме поверхности ограничения
• Анкор: Системы ограничения
• Дата: 28.03.2022
• Размер: 4.57 Mb.
• Имя файла: Текст монографии.doc
• Тип: Анализ; #422574
• страница: 14 из 22

Глава 4. Алгоритмы адаптивного ограничения ТРАЕКТОРНЫХ параметров ДВИЖЕНИЯ

летательных аппаратов

4.1. Общий случай ограничения траектории движения

летательного аппарата в трехмерном пространстве состояний

4.1.1. Содержательная постановка задачи

Пусть в нормальной системе координат 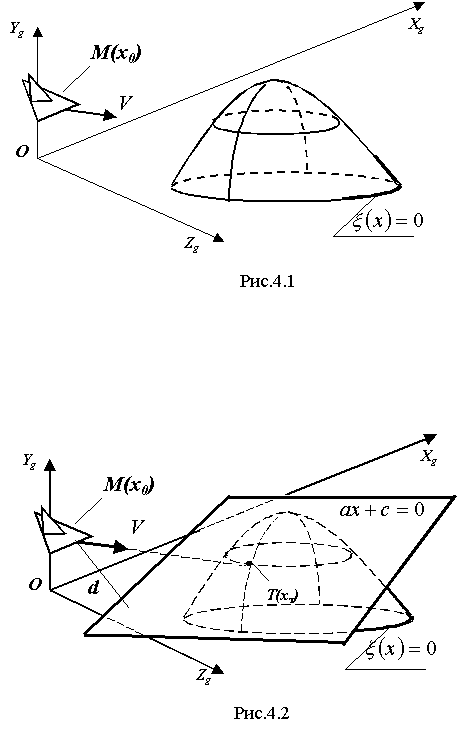определены (см. рис.4.1): выпуклая поверхность ограничения, заданная уравнением

, (4.1)

точка с текущими координатами летательного аппарата, получаемыми либо с использованием цифровой карты местности, либо методами точной навигации (в данной работе эти вопросы не рассматриваются), известны значения измеряемых на борту ЛА пилотажных параметров движения.



Рис.4.1

Требуется: при угрозе столкновения ЛА с поверхностью ограничения, аппроксимированной уравнением (4.1), обеспечить уклонение самолета от нее. Управление самолетом в процессе увода осуществляется в каналах тангажа, крена и курса. При этом предполагается, что команды управления вырабатываются системой ограничения в рамках доверенного ей управления.

4.1.2. Модель объекта и поверхности ограничения

Зададим модель пространственного движения летательного аппарата в виде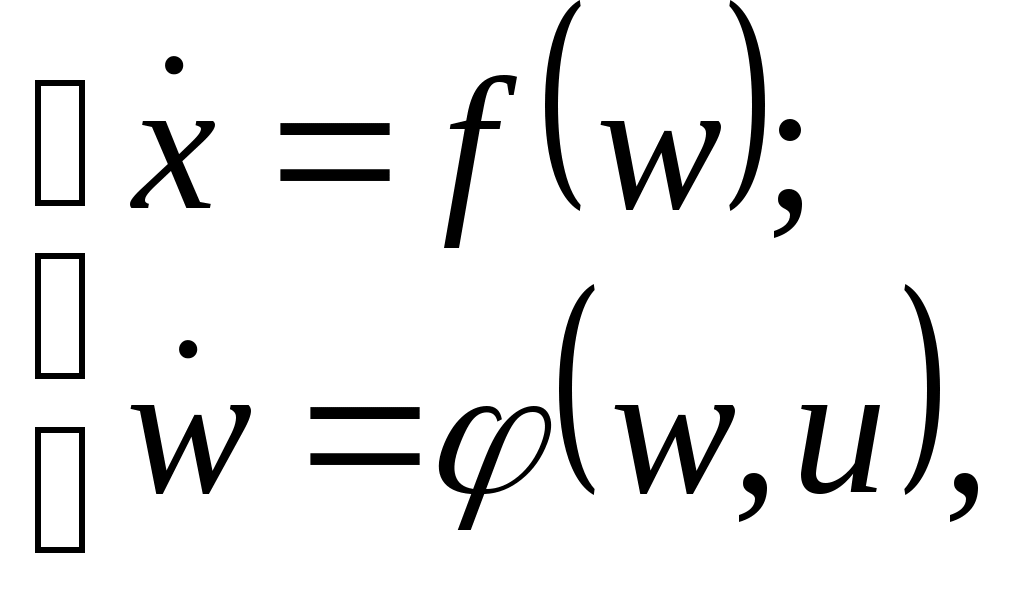

(4.2)

где - вектор, характеризующий положение центра масс самолета в нормальной системе координат; - вектор, задающий модуль и ориентацию скорости летательного аппарата относительно нормальной системы координат ; - вектор управления; , - векторные функции указанных векторных аргументов.

Заметим, что в системе (4.2) управление u оказывает непосредственное влияние на вектор параметров w, а на вектор x – влияние опосредовано через вектор w, то есть вектор w является псевдоуправлением для вектора x, совокупность параметров которого подлежат ограничению.

Доверим системе ограничения некоторым образом заданное управление

(4.3)

и воспользуемся методикой синтеза ее алгоритмов, изложенной для детерминированной непрерывной управляемой многоуровневой динамической системы (см. главу 2).

Для упрощения выкладок воспользуемся, изложенным подходом к описанию границы поверхности ограничения. А именно, в точке прогнозируемого столкновения самолета с поверхностью ограничения строится касательная плоскость, которая и принимается в качестве плоскости ограничения. Такой подход допустим вследствие цикличной работы алгоритма ограничения. Если ограничиться рассмотрением линейного прогноза траектории движения самолета, то координаты точки прогнозируемого столкновения Т (см. рис.4.2) определяются путем совместного решения уравнений поверхности ограничения (4.1) и линии, содержащей вектор скорости самолета.



Рис.4.2

Каноническое представление последней имеет вид

, (4.4)

где , , - проекции вектора скорости на оси нормальной системы координат.

Тогда, согласно [25], плоскость, касательная к поверхности ограничения в точке Т(х_т), может быть представлена уравнением

, (4.5)

где

; .

При эволюциях летательного аппарата в пространстве, вследствие управляющих действий летчика, САУ или системы ограничения, изменяются координаты точки . Это в свою очередь приводит к необходимости цикличного перерасчета параметров плоскости ограничения, определяемых матрицей строкой а и скаляром с.