Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения

• Название: Адаптивность к свойствам объекта, форме поверхности ограничения
• Анкор: Системы ограничения
• Дата: 28.03.2022
• Размер: 4.57 Mb.
• Имя файла: Текст монографии.doc
• Тип: Анализ; #422574
• страница: 10 из 22

2.4.3. Алгоритм ограничения детерминированной

непрерывной управляемой многоуровневой

динамической системы

Широкий класс динамических систем, в том числе и описание траекторного движения ЛА, допускает при описании использовать многоуровневую систему векторных дифференциальных уравнений в форме Коши. Рассмотрим двухуровневую ДС, представленную в виде

(2.44)

где - вектор состояния ДС; - вектор псевдоуправления для вектора x; - вектор действительных управлений; и - векторные функции векторных и скалярного аргумента соответствующей размерности. Система (2.44) может быть получена путем декомпозиции модели (2.1) методом, изложенным в [2].

Рассмотрим получение основных расчетных зависимостей для адаптивной системы ограничения, алгоритм функционирования которой представлен условием (2.20). Пусть при этом граничная гиперплоскость, являющаяся касательной к поверхности ограничения , заданной в пространстве , описана уравнением (2.34), а расстояние до нее – уравнением (2.35). Найдем первую и вторую производные от расстояния d, величину , а также компенсационное управления . Продифференцировав по t выражение (2.35) и подставив вместо правую часть первого уравнения системы (2.44) имеем

. (2.45)

Повторное дифференцирование по t с учетом (2.44) дает следующее выражение

. (2.46)

Положив в векторной функции уравнения (2.46) получим

. (2.47)

И, наконец, записав в приращениях выражение (2.46) и выразив из него величину имеем

, (2.48)

где

.

В итоге для алгоритма работы системы выдерживания ограничений (2.20) получены его составляющие, а именно .

Таким образом, в спектре описания динамических систем детерминированными непрерывными моделями получена алгоритмическая основа решения задач адаптивного ограничения вектора состояния ДС. Последующие главы посвящены конкретным случаям ограничения параметров движения и их совокупности такой сложной динамической системы, как летательный аппарат.

Глава 3. Алгоритмы адаптивного ограничения

пилотажных параметров летательных

аппаратов

3.1. Адаптивное ограничение угла атаки маневренного самолета

В первом разделе рассматривались недостатки системы ограничения угла атаки с фиксированной настройкой параметров. Применим метод адаптивного ограничения компонент вектора состояния динамической системы к задаче ограничения угла атаки в изолированном продольном движении.

Пусть продольное короткопериодическое движение самолета описывается системой уравнений второго порядка вида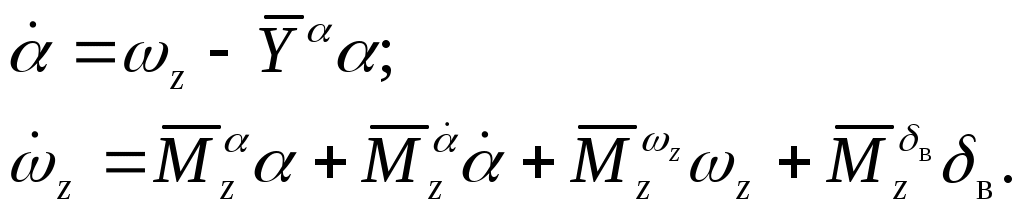

(3.1)

В (3.1) все обозначения общепринятые.

Для отработки методических вопросов синтеза алгоритмов системы ограничения система управления самолетом задана совокупностью управлений от летчика, демпфера тангажа и автомата продольной устойчивости по углу атаки

. (3.2)

Коэффициенты в (3.2) являются функциями режима полета, то есть

.

Будем полагать, что ограничение в координатах имеет вид представленный на рис.3.1. Его также можно описать матричным уравнением

, (3.3)

где ; ; .

При этом превышение недопустимо из условий обеспечения безопасности полета самолета.

Расстояние от точки, характеризующей текущее состояние объекта ограничения до границы (3.3) определяется выражением (2.35). Сделав соответствующие подстановки, для рассматриваемого случая получим очевидное равенство


. (3.4)

Зададим управление ограничение в виде соответствующем закону (2.20)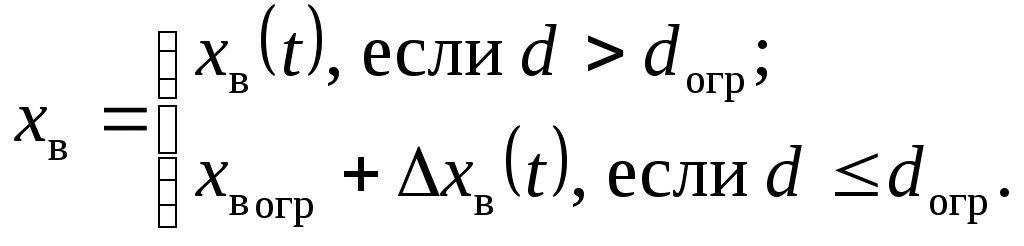

(3.5)

Здесь - доверенное системе ограничения отклонение ручки управления самолетом на пикирование; - компенсационное управление; - расстояние до границы , при котором необходимо включать управление ограничения, определяется по зависимости (2.14).

В соответствии с изложенным методом, найдем первую и вторую производные от расстояния d, величину , а также компенсационное управление . Из (3.4) очевидно, что

(3.6)

Для получения компоненты уравнения (2.14) 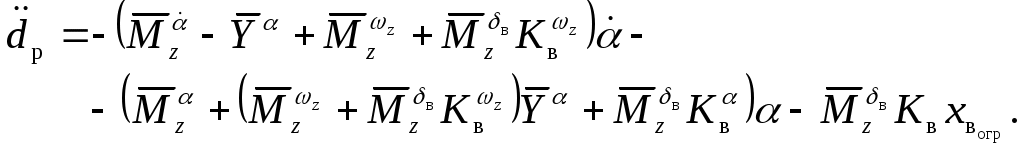поступим следующим образом. Перепишем систему уравнений (3.1) в виде "вход – выход". Тогда с учетом (3.2) и подставив вместо управление ограничения имеем

(3.7)

В итоге выражение, определяющее момент срабатывания системы ограничения угла атаки примет следующий вид

, (3.8)

где коэффициент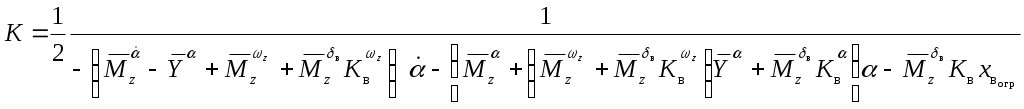

и зависит от:

• 
  собственных свойств самого объекта, с учетом системы улучшения устойчивости и управляемости;
  
• 
  доверенного системе управления ограничения;
  
• 
  эффективности управления;
  
• 
  текущих значений и .
  

Заметим, что структура выражения (3.8) существенно отличается от традиционно принятой

, (3.9)

где .

Во-первых, вместо первой степени темпа изменения угла атаки в (3.9) в (3.8) используется квадрат этой величены. Во-вторых, коэффициент К стал вычисляемым коэффициентом. Причем, даже при изменении в результате возможных отказов собственных свойств объекта ограничения, его характеристик устойчивости и управляемости, алгоритм ограничения соответствующим образом подстраивается к новым условиям. Это достигается с помощью процедуры текущей идентификации отказов, например, с использованием метода, подробно рассмотренного в работах [4, 21].

Помимо этого, для поддержания на этапе ограничения в законе управления (3.5) присутствует слагаемое , определяющее компенсационное управление и обеспечивающее на этапе ограничения. Компенсационное управление можно получить, переписав (3.7) в приращениях, а именно

.

Проведя соответствующие преобразования, имеем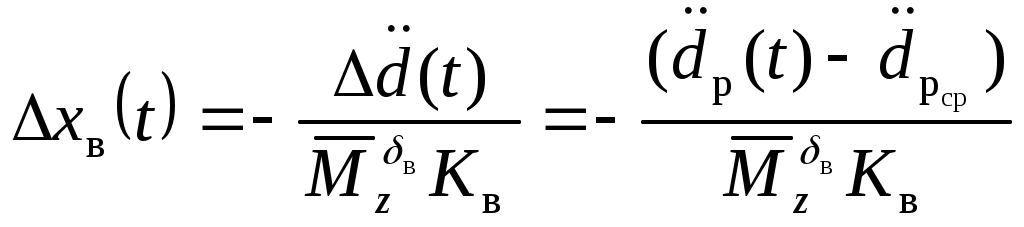

. (3.10)

Необходимо отметить, что аналогичные развернутые выражения для , , можно получить, воспользовавшись зависимостями (2.41), (2.42), (2.43).

Использование (3.5), (3.8) и (3.10) обеспечивает строгое решение задачи ограничения угла атаки с полным учетом всех основных факторов, влияющих на динамику движения ЛА.

Рассмотрим модельную задачу ограничения угла атаки маневренного самолета с использованием изложенных алгоритмов.

В качестве математической модели объекта управления воспользуемся системой (3.1), функционирующей совместно с законом управления (3.2). Пусть самолет получил управление , направленное на увеличение угла атаки, и есть угроза выхода за . В каждый момент времени в соответствии с (3.4) и (3.8) производится оценка величин d и , и их сравнение. В случае если летчик принудительно выключается из контура управления и включается управление ограничения. Его реализация описана уравнениями (3.5) и (3.10).

Отключение алгоритма ограничения возможно, например, при достижении условия 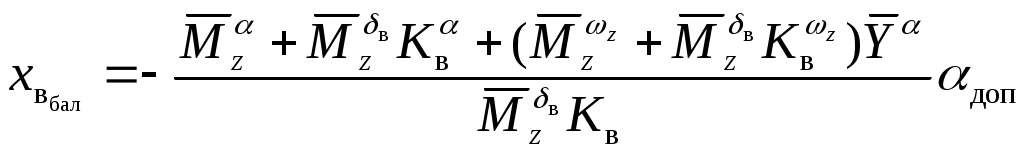. При этом ручка управления самолетом переводится в балансировочное положение . Значение может быть получено из (3.7), приравняв его к нулю и положив . В итоге

. (3.11)

Могут применяться и другие условия и методики отключения системы ограничения угла атаки.

На рис.3.2 представлены результаты решения модельной задачи ограничения угла атаки на уровне 24° при различных начальных настройках системы ограничения и идеальных рулевых приводах.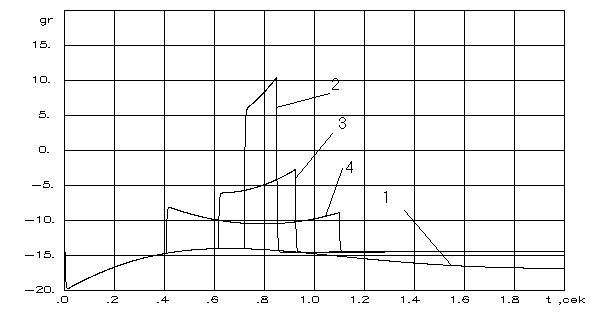



1 – переходный процесс при отсутствии системы ограничения;

2 - = 0 град; 3 - = -12 град; 4 - = - 15 град.

Рис.3.3

Причем на график выводилось не отклонение ручки управления самолета, а отклонение по времени стабилизатора . Это делалось с целью иллюстрации работы системы улучшения устойчивости и управляемости, наряду с системой ограничения.

Из рисунка видно, что чем меньше значение управления ограничения – угловое положение, в которое переводится стабилизатор, тем раньше система ограничения вступает в работу и тем больше по времени проходит процесс ограничения.

На рис.3.3 представлены результаты моделирования процесса ограничения угла атаки на уровне 24º при различных исходных скоростях полета. Налицо адаптивные свойства алгоритма к изменению режима полета.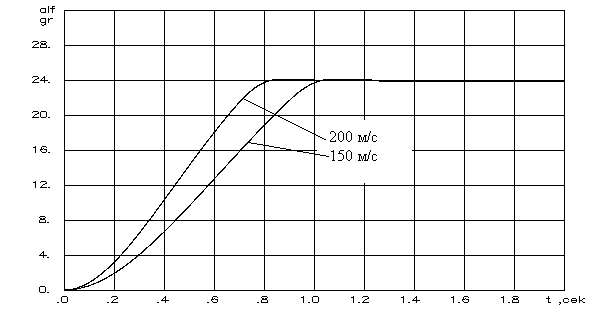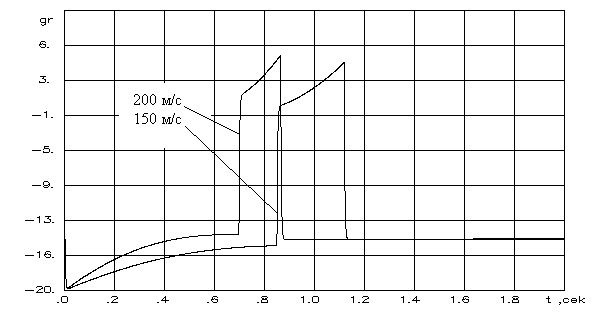





Рис.3.3

Оценка алгоритма ограничения на робастность к исходной информации о собственных свойствах объекта производилась путем загрубления его аэродинамических характеристик. Так, на рис.3.4 приведены результаты моделирования процесса ограничения угла атаки при различных значениях аэродинамического коэффициента , а на рис.3.5 – коэффициента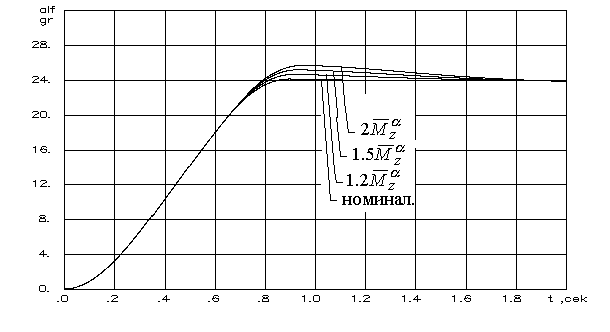



Рис.3.4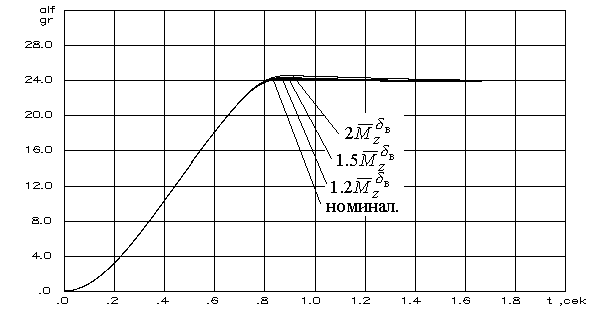



Рис.3.5
Из приведенных рисунков видно, что даже двукратная ошибка в настройке указанных коэффициентов приводит к превышению допустимого угла атаки лишь на 5 … 8%. Ошибки в настройке других коэффициентов оказывают еще меньшее влияние. Это свидетельствует о робастности алгоритма ограничения угла атаки к ошибкам моделирования.

Очевидно, что традиционная схема алгоритма ограничения угла атаки не обладает продемонстрированными возможностями. Ее применение эффективно только в узком диапазоне настроечных режимов. Таким образом, полученный алгоритм адаптивного ограничения угла атаки обладает явными преимуществами перед аналогичными традиционными схемами выдерживания угла атаки.