Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения

• Название: Адаптивность к свойствам объекта, форме поверхности ограничения
• Анкор: Системы ограничения
• Дата: 28.03.2022
• Размер: 4.57 Mb.
• Имя файла: Текст монографии.doc
• Тип: Анализ; #422574
• страница: 18 из 22

4.4. Особенности выдерживания нестационарных

ограничений

При исследовании траекторных задач и в реальной практике нередки случаи необходимости ограничения параметров полета в зависимости от наличия движущихся объектов различной природы. Это, например, летящий на пересекающихся курсах самолет, зона осколков от применяемых средств поражения, зоны грозовой деятельности и тому подобное. Решению этой проблемы были посвящены ряд работ [2,5,7,8,9,23]. Однако в полном объеме задача не решена. В данном параграфе на достаточно простом, но не тривиальном примере показана применимость изложенного метода к решению проблемы ограничения нестационарной границы.

Пусть две материальные точки, причем одна из них управляемая, двигаются навстречу друг другу. Уравнения, описывающие их движение, представлены в следующем виде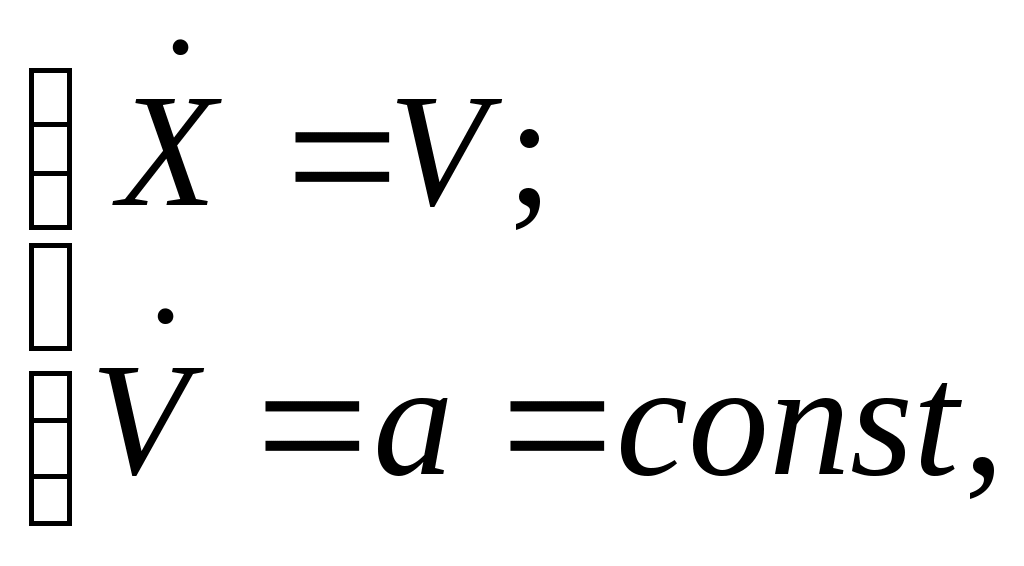

• 
  уравнения движения управляемого объекта ограничения
  

(4.45)

• 
  уравнения движения границы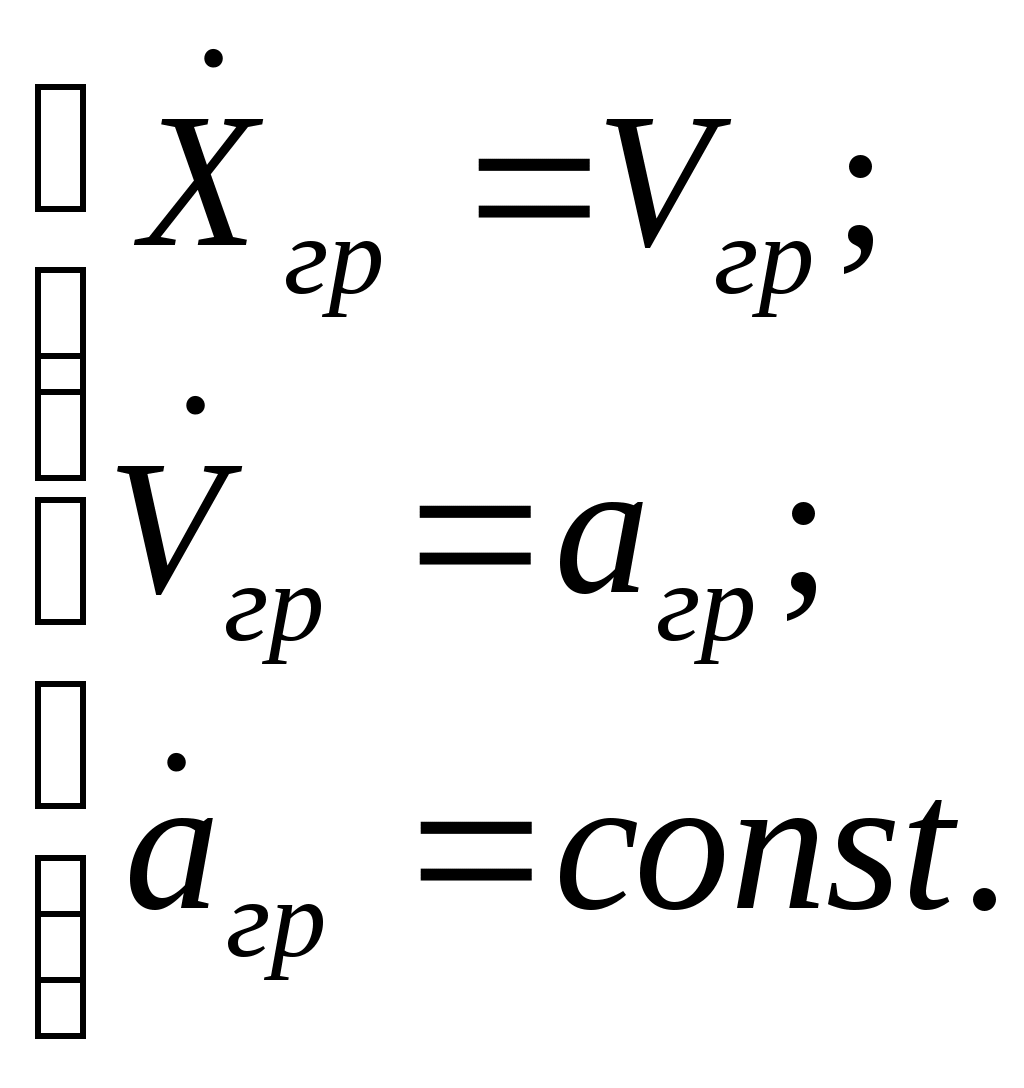
  

(4.46)

Требуется определить расстояние между объектом и движущейся границей, при достижении которого необходимо включить заданное управление ограничения для объекта (4.45). Все параметры движения нестационарной границы считаются известными.

Согласно методу ограничения дальность до границы определиться как

, (4.47)

первая производная от дальности:

, (4.48)

ускорение торможения, при условии включения управления ограничения :

, (4.49)

компенсационное управление на этапе ограничения:

. (4.50)

где - ускорение границы в момент включения алгоритма ограничения.

В итоге искомое расстояние включения алгоритма ограничения находится в соответствии с выражением

. (4.51)

Моделирование процесса ограничения по приведенным алгоритмам иллюстрируется рис.4.15.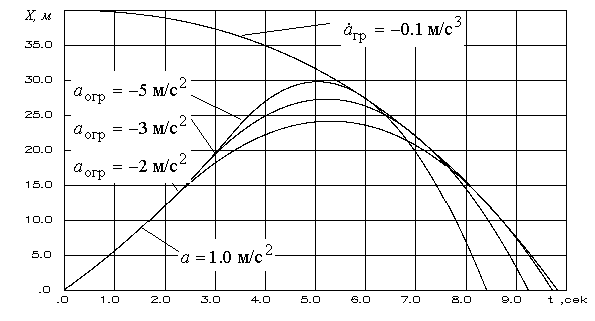



Рис.4.15

Из приведенных результатов видно, что алгоритм ограничения работоспособен и при рассмотрении нестационарной границы. Чем больше управление ограничения, тем быстрее объект может подойти к ней. Однако для обеспечения процесса ограничения необходимо знать параметры движения самой границы.

Данный подход может быть применим и для более сложных случаев описания, как границы ограничения, так и объекта управления.

Глава5. увод самолета от поверхностей ограничения по програмМируемым траекториям

5.1. Содержательная постановка задачи

В данном разделе представлен подход к построению алгоритмов систем выдерживания ограничений в траекторном контуре управления летательным аппаратом, основанный на предварительном задании траектории движения ЛА.

Использование такого подхода явилось следствием специфических действий человека как оператора в стрессовых ситуациях, причем известно, что деятельность экипажа в полете на малой высоте относится к первому типу экстремальных ситуаций.

С учетом психологии летчика очевидно, что автоматический увод самолета от земной поверхности должен производится с помощью выполнения только восходящих маневров (возможны и маневры увода строго в горизонтальной плоскости, но только не нисходящие). На рис.5.1 схематично показан пример задачи ограничения, где рассмотренные выше алгоритмы будут стремиться произвести увод от границы нисходящим маневром – линия 1 на рисунке, в отличие от желаемого – линия 2.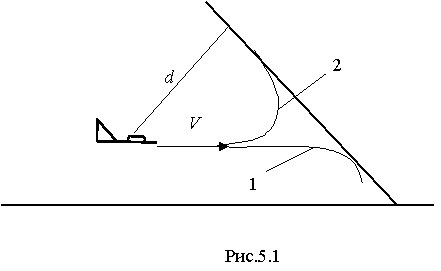



Рис.5.1

Для решения указанной проблемы рассмотрим схему увода самолета в нормальной системе координат от поверхности ограничения, заданной уравнением

(5.1)

и введем следующие обозначения (см. рис. 5.2):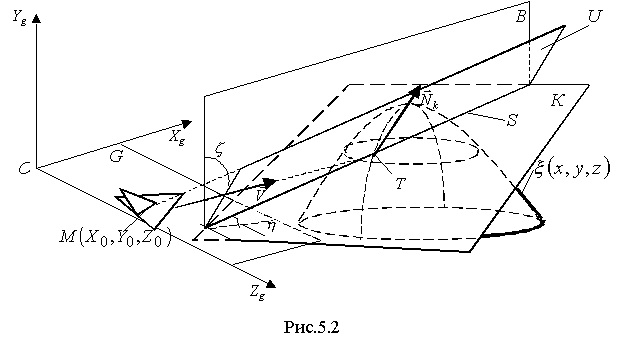

- точка с текущими координатами летательного аппарата; - точка на поверхности ограничения, получаемая пересечением линии продолжения вектора скорости самолета с поверхностью; К - плоскость, касательная к поверхности ограничения в точке Т; U - некоторая плоскость, в которой осуществляется маневр уклонения от препятствия, содержащая нормаль к поверхности в точке Т; В и G - вертикальная и горизонтальная плоскость соответственно; S – прямая пересечения плоскости увода U с плоскостью К; ζ – угол между плоскостью U и вертикальной плоскостью В; η – угол между прямой S и горизонтальной плоскостью G.



Рис.5.2

Управление самолетом в процессе увода осуществляется в каналах крена и тангажа с целью вывода объекта в плоскость увода U и его разворота в ней с максимально располагаемыми возможностями до совмещения траектории полета самолета с линией S. При этом предполагается, что командные сигналы управления вырабатывает система предупреждения столкновения самолета с земной поверхностью.