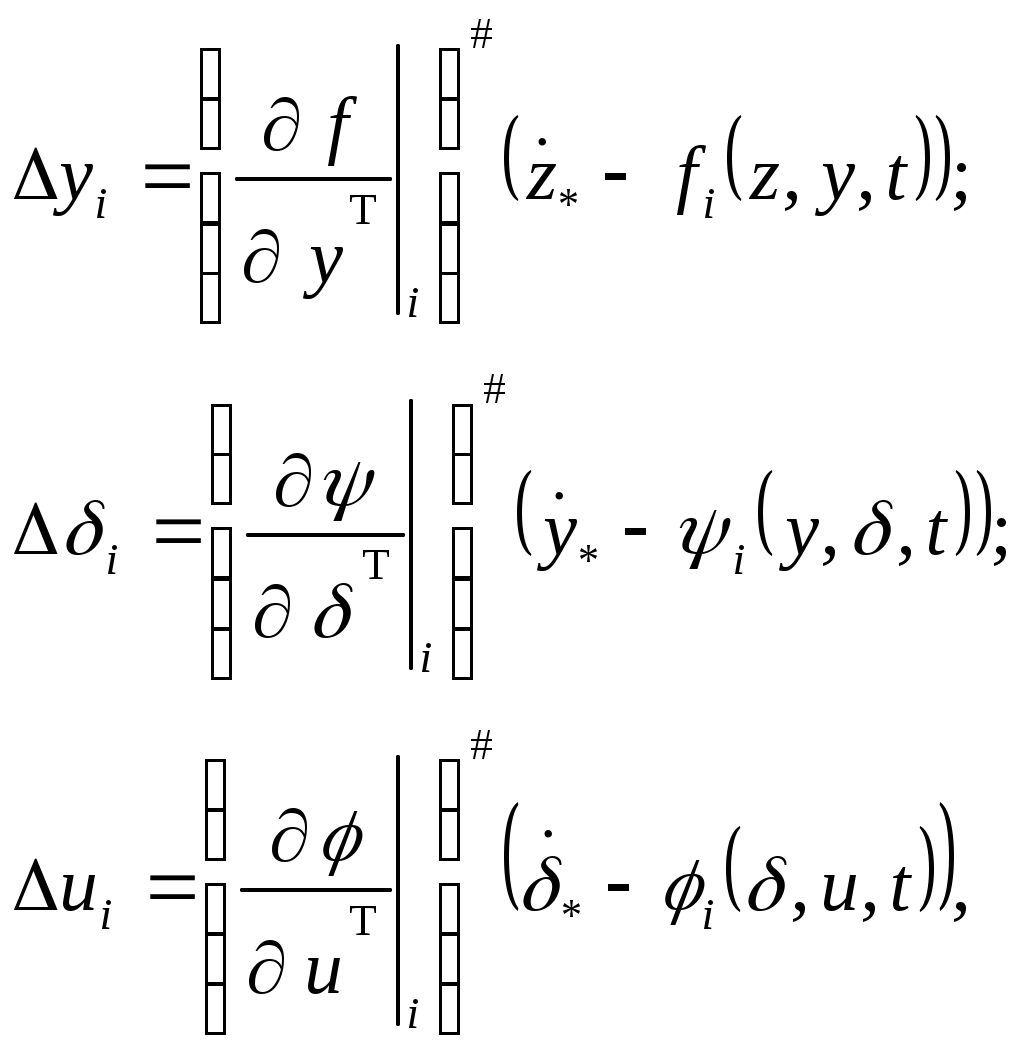|
|
Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения
5.4. Формирование управлений
Рассмотрим динамический объект вида
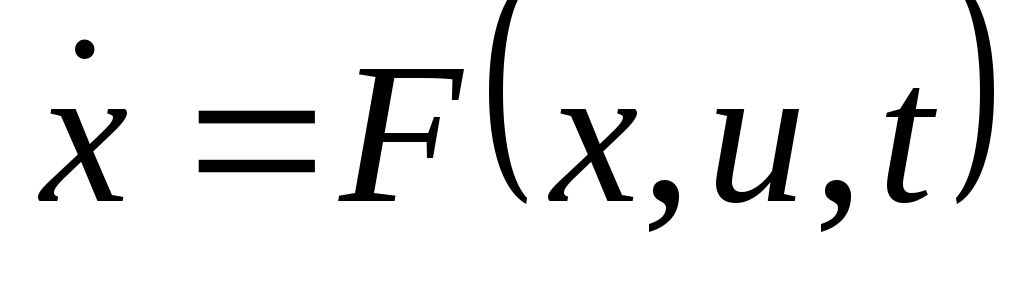 , (5.16) , (5.16)
где: 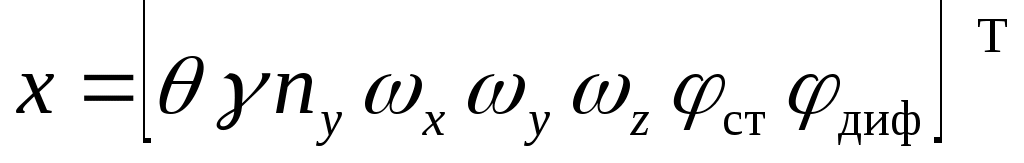 - вектор состояния; - вектор состояния; 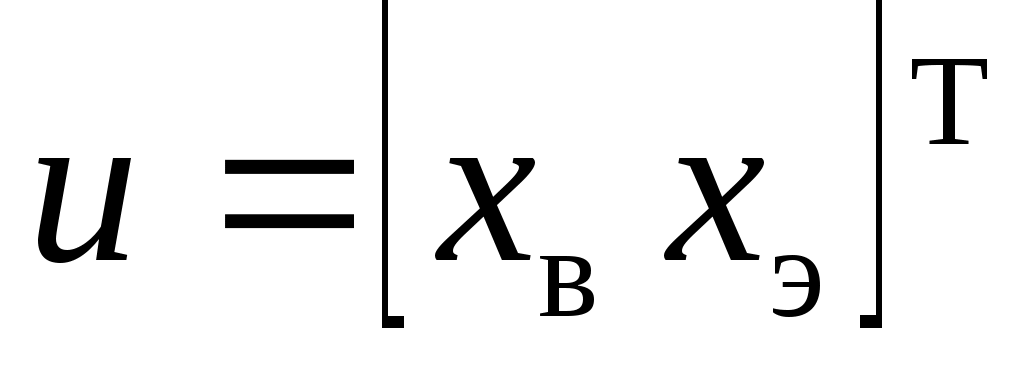 - вектор управлений. - вектор управлений.
Представим уравнения, входящие в систему (5.16), в виде трехуровневой иерархии систем уравнений
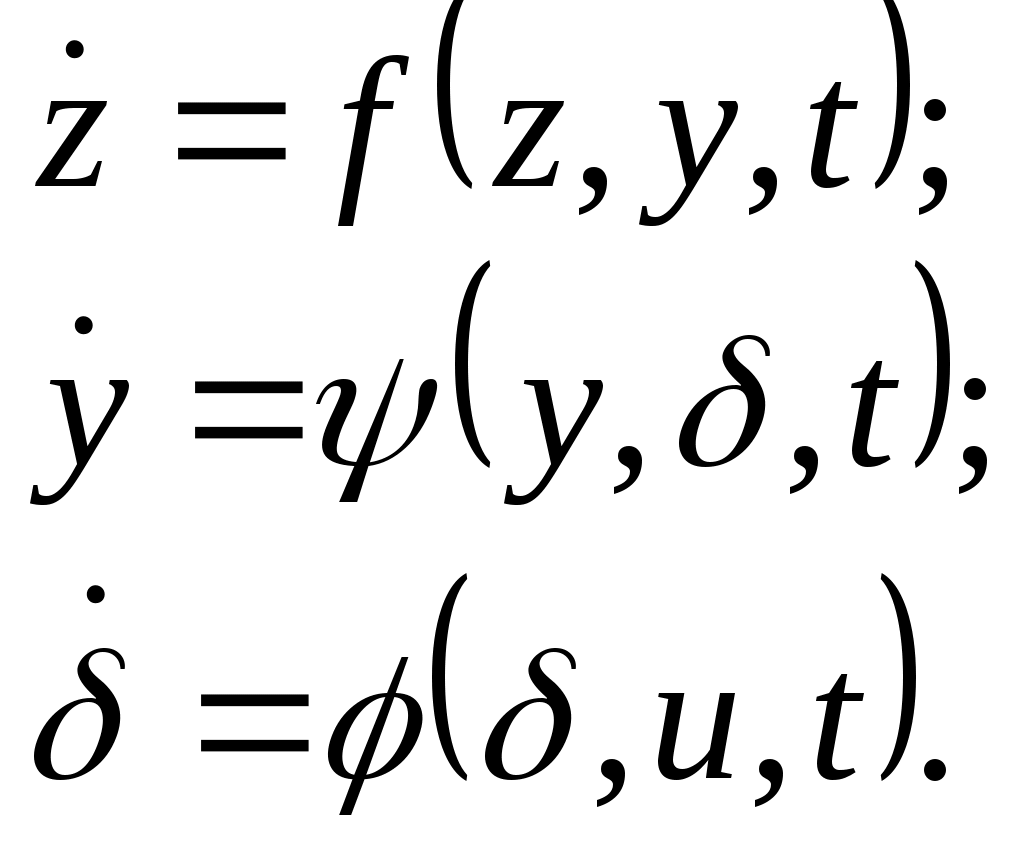 (5.17) (5.17)
Первый уровень иерархии представлен заданными траекторными параметрами самолета, входящими в вектор состояния 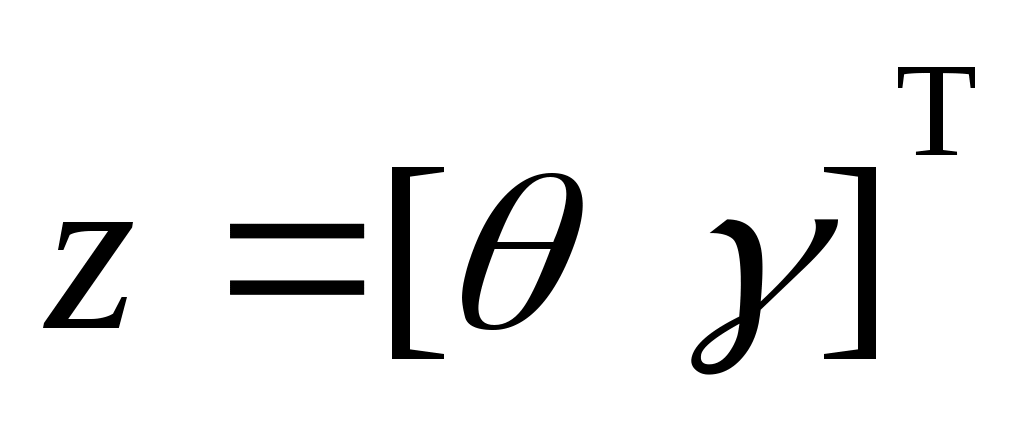 , и вектором псевдоуправления , и вектором псевдоуправления 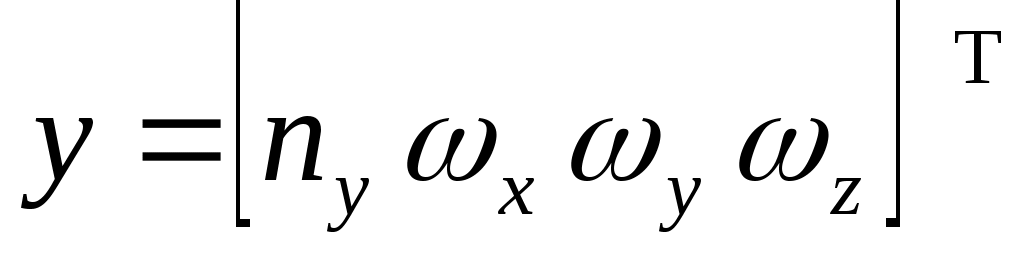 . Второй уровень - пилотажными параметрами самолета, входящими в вектор состояния y, и вектором псевдоуправлений . Второй уровень - пилотажными параметрами самолета, входящими в вектор состояния y, и вектором псевдоуправлений 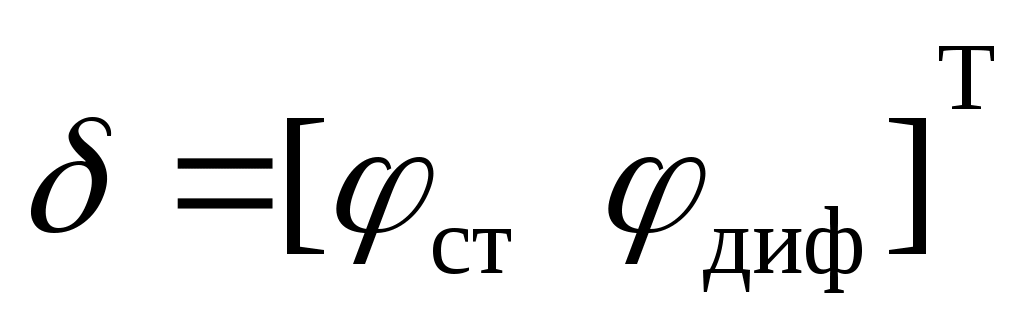 . Третий уровень - системой предотвращения столкновения самолета с земной поверхностью в части отклонения рулевых поверхностей с учетом реальных свойств рулевых приводов самолета. Здесь δ - вектор состояния системы, . Третий уровень - системой предотвращения столкновения самолета с земной поверхностью в части отклонения рулевых поверхностей с учетом реальных свойств рулевых приводов самолета. Здесь δ - вектор состояния системы, 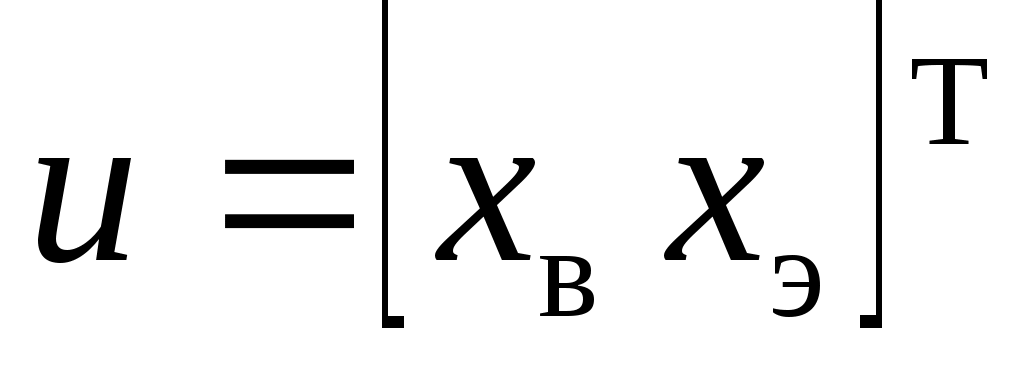 - искомый вектор управлений. - искомый вектор управлений.
В соответствии с основными положениями метода прямой оптимизации, определение необходимых для увода самолета от поверхности ограничения приращений псевдоуправлений 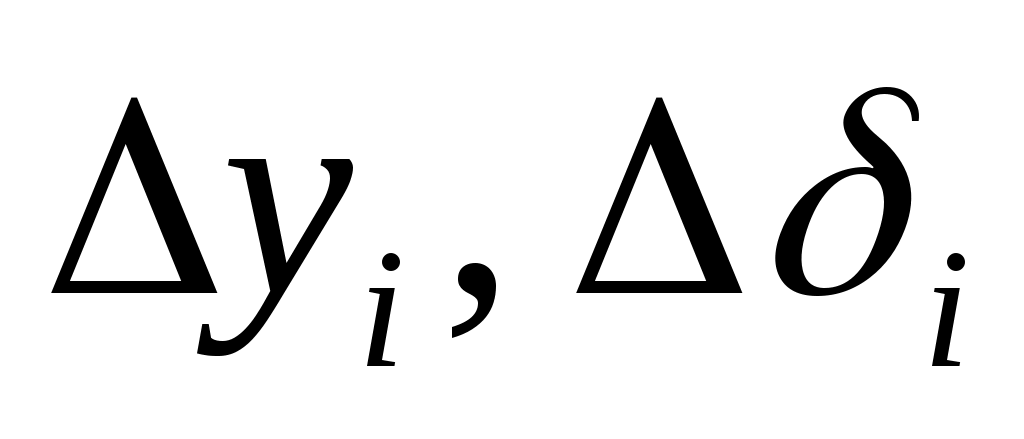 и управляющих функций и управляющих функций 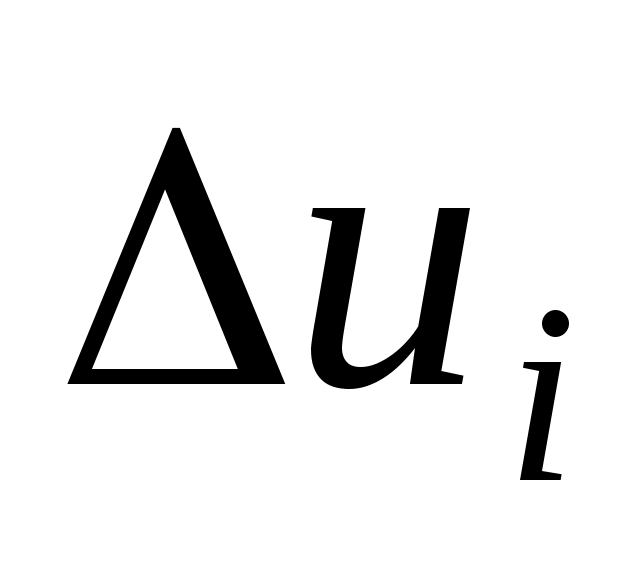 проводится с использованием соотношений: проводится с использованием соотношений:
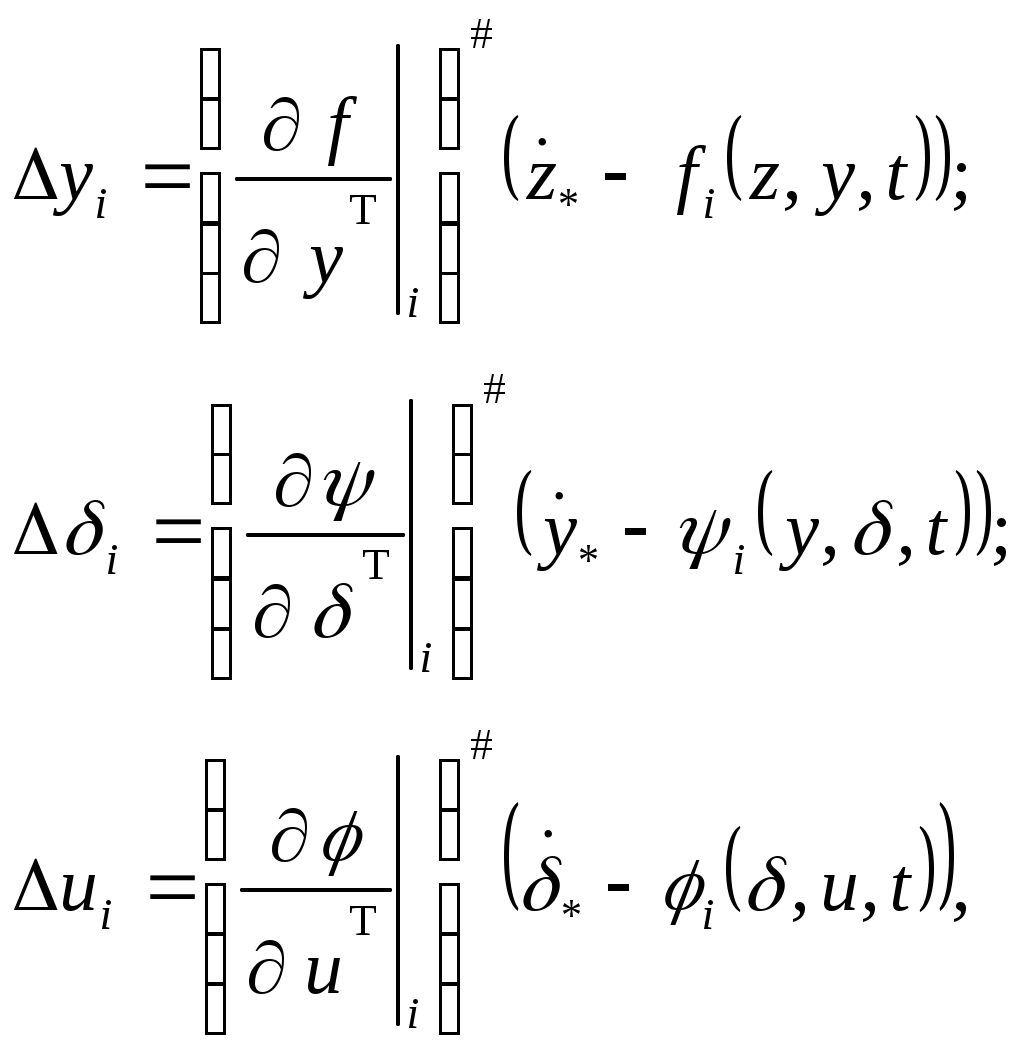
где # – знак псевдообращения;  , , 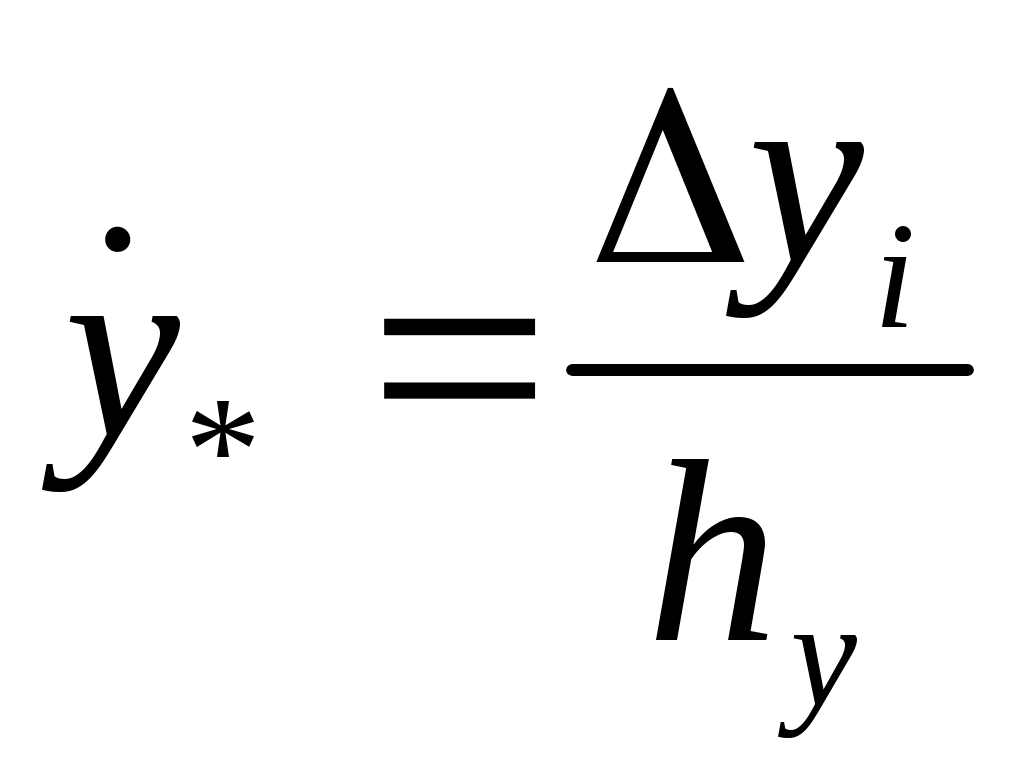 , , 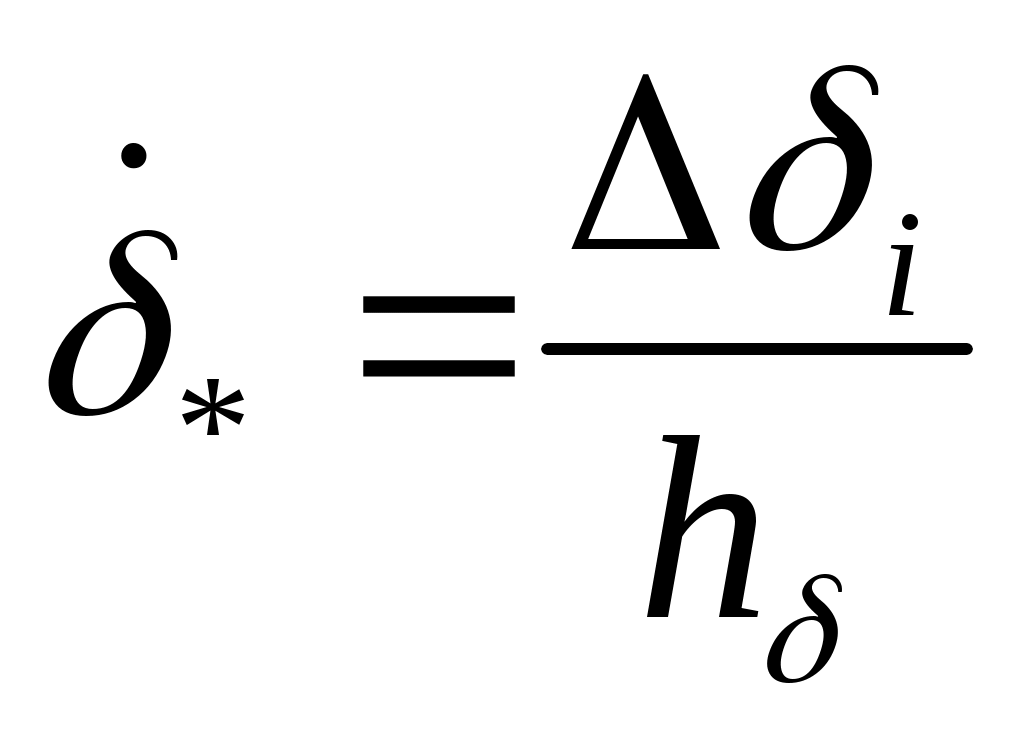 – потребные значения векторов скорости, определяемые на каждом i-м шаге из условия достижения системой состояния – потребные значения векторов скорости, определяемые на каждом i-м шаге из условия достижения системой состояния 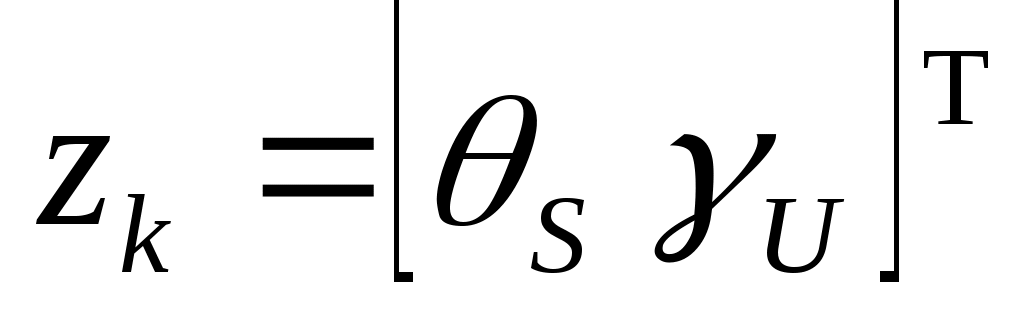 ; ; 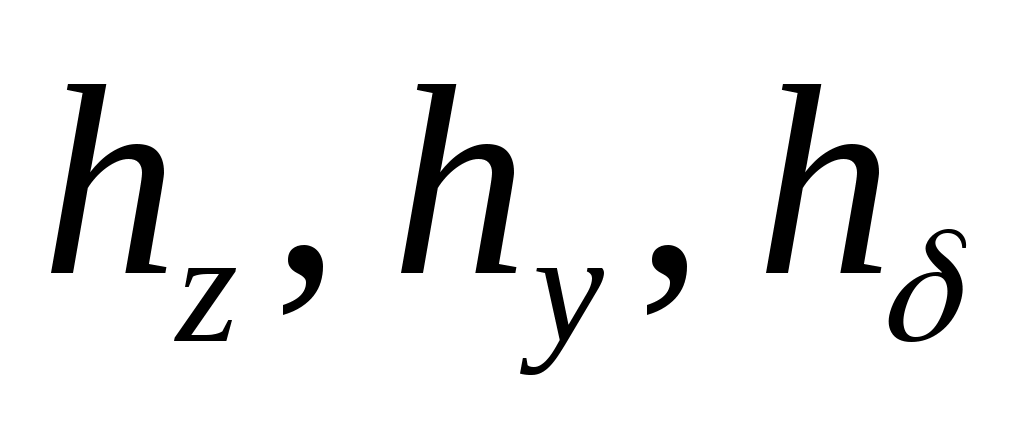 - интенсивности управлений, задаются исходя из приемлемого качества переходных процессов; - интенсивности управлений, задаются исходя из приемлемого качества переходных процессов; 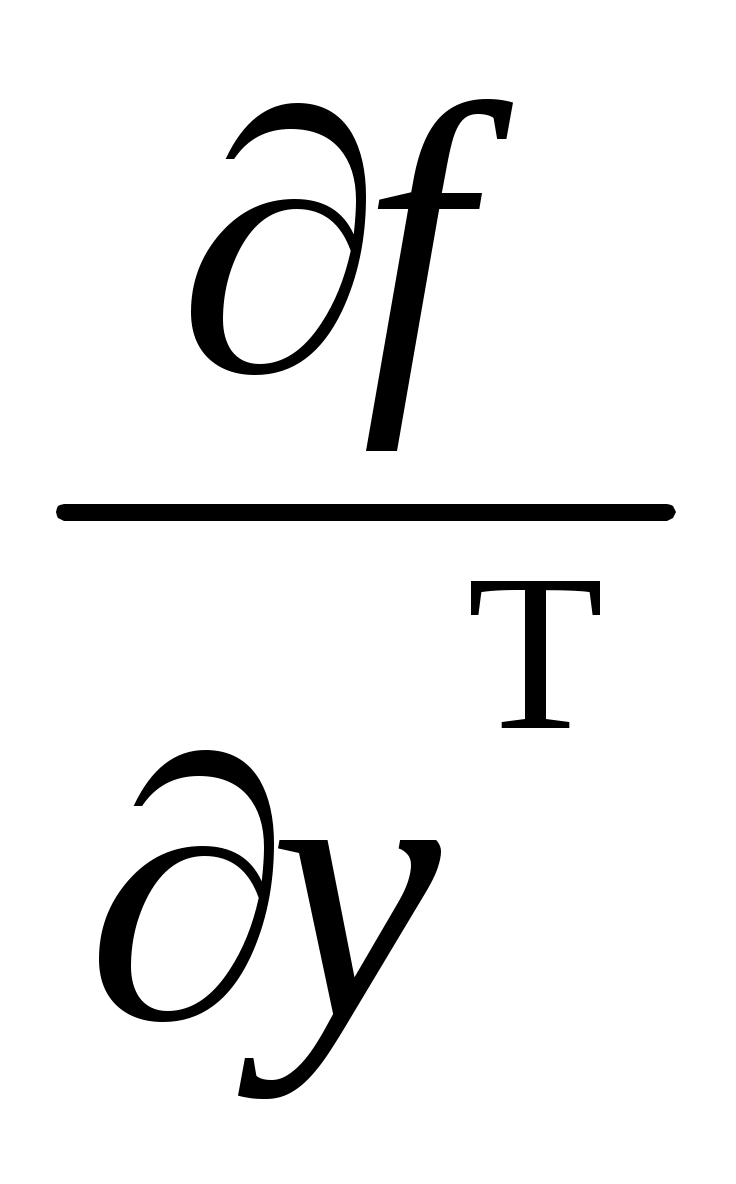 , , 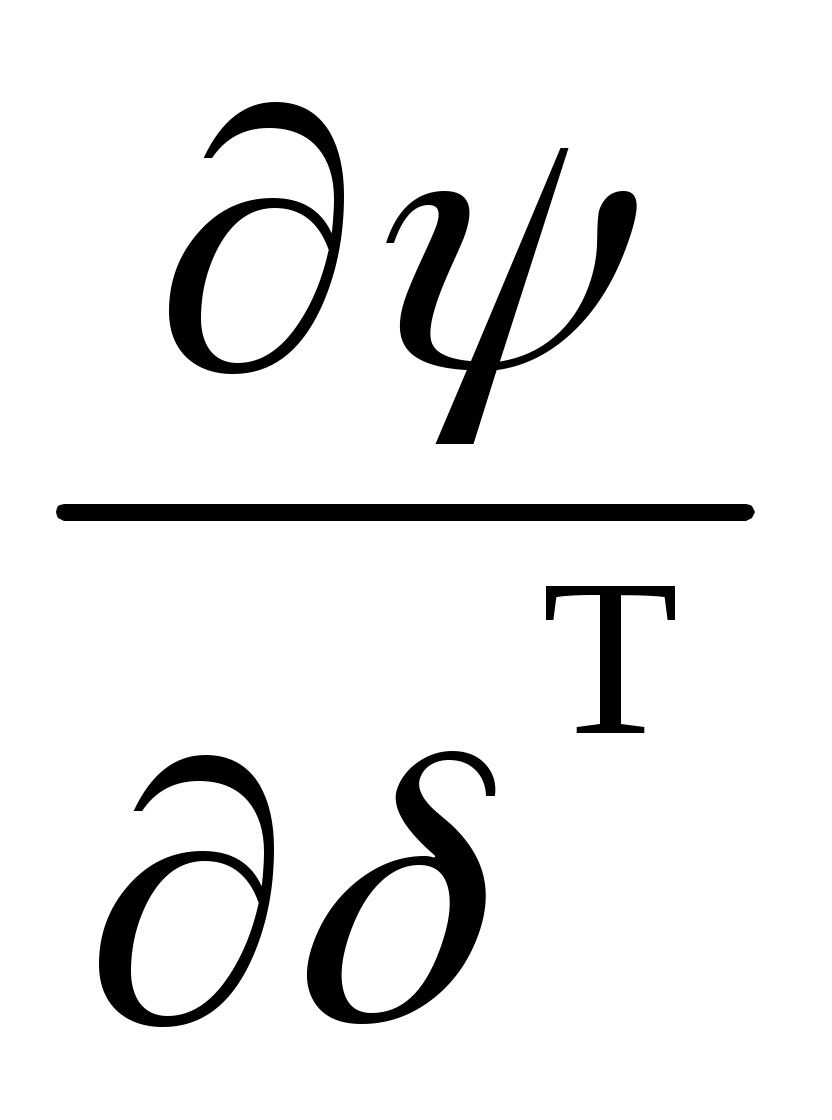 , , 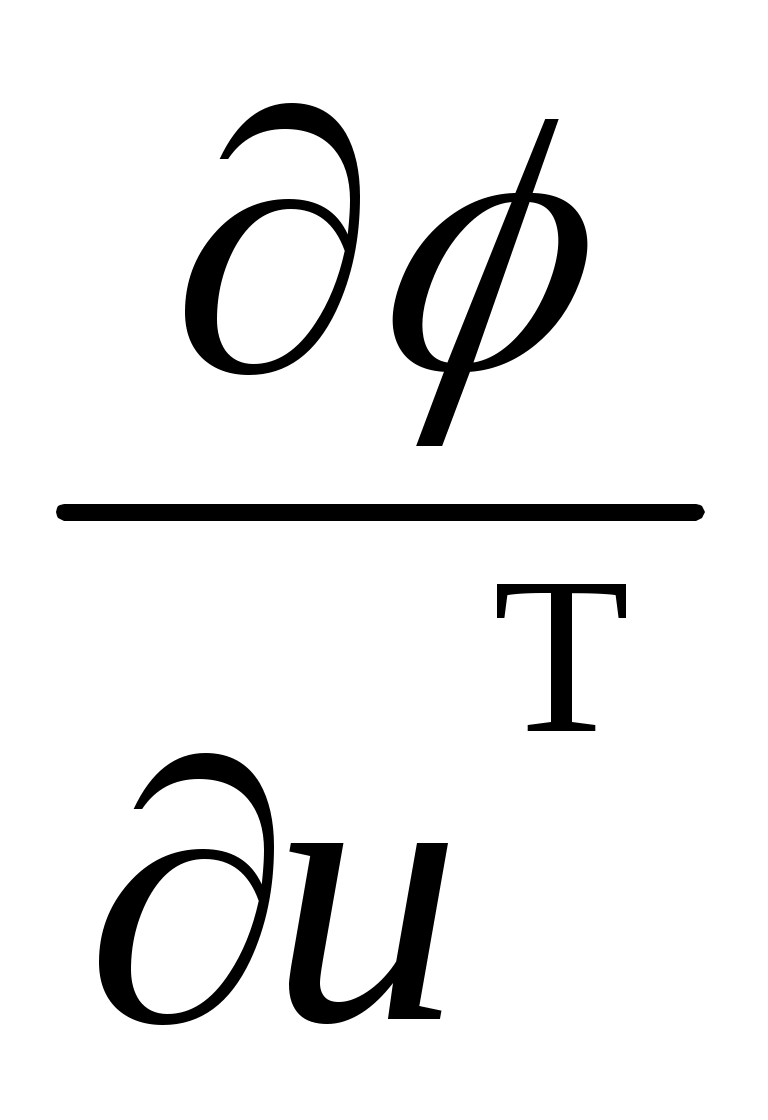 – матрицы частных производных, пересчитываются на каждом i-м шаге формирования управлений. – матрицы частных производных, пересчитываются на каждом i-м шаге формирования управлений.
В данном параграфе представлены результаты моделирования движения маневренного самолета в условиях возможного столкновения с различного вида поверхностями ограничения. Использовалась исходная информация о его типовых аэродинамических, динамических, геометрических и массовых характеристиках, изложенная в [16].
5.5.1. Вертикальная стенка
Пусть ЛА движется из начальной точки пространства М (рис.5.6) с координатами (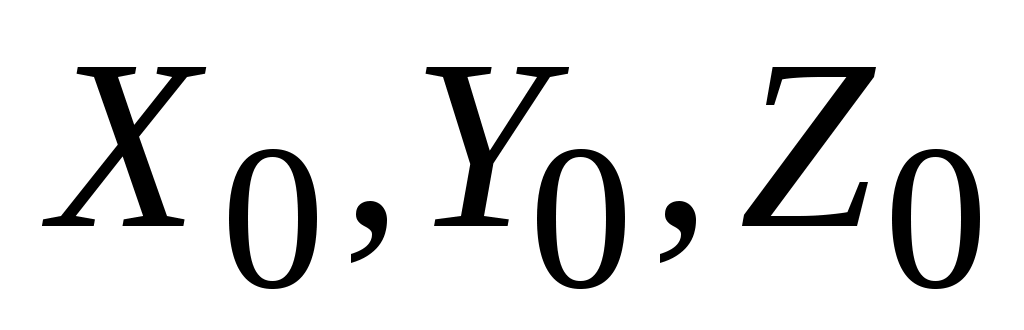 ). При этом известны параметры его движения: скорость полета ). При этом известны параметры его движения: скорость полета 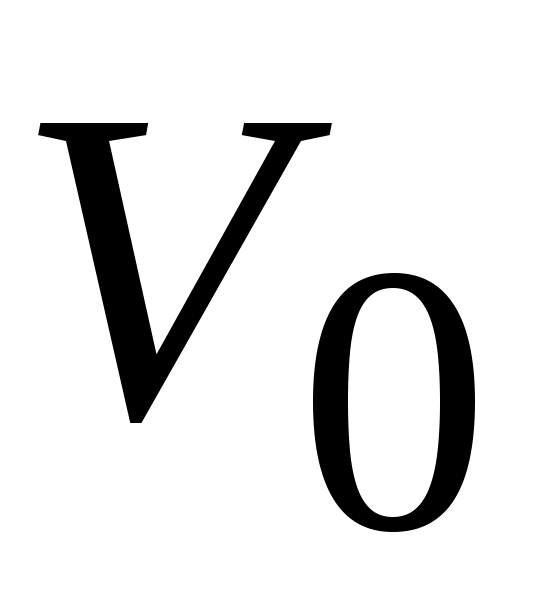 , угол наклона траектории , угол наклона траектории 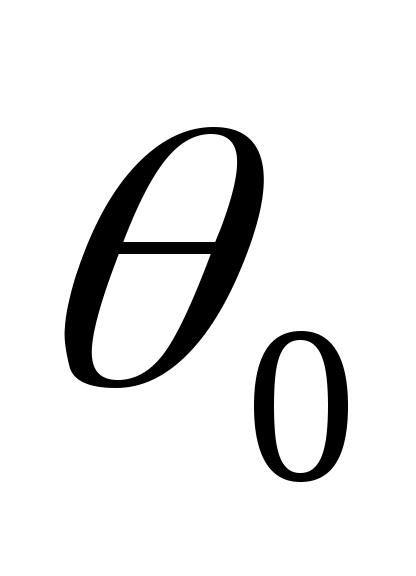 , крен , крен 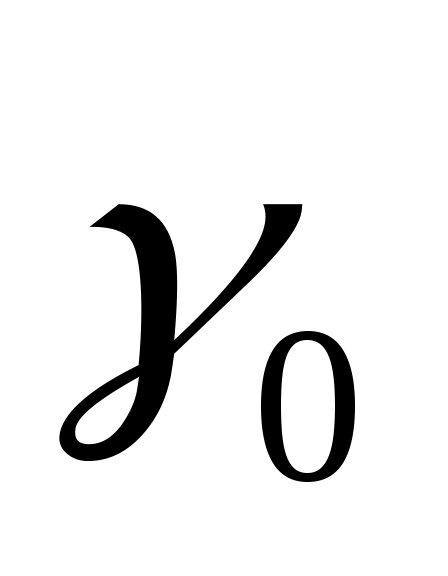 и максимальная располагаемая перегрузка и максимальная располагаемая перегрузка 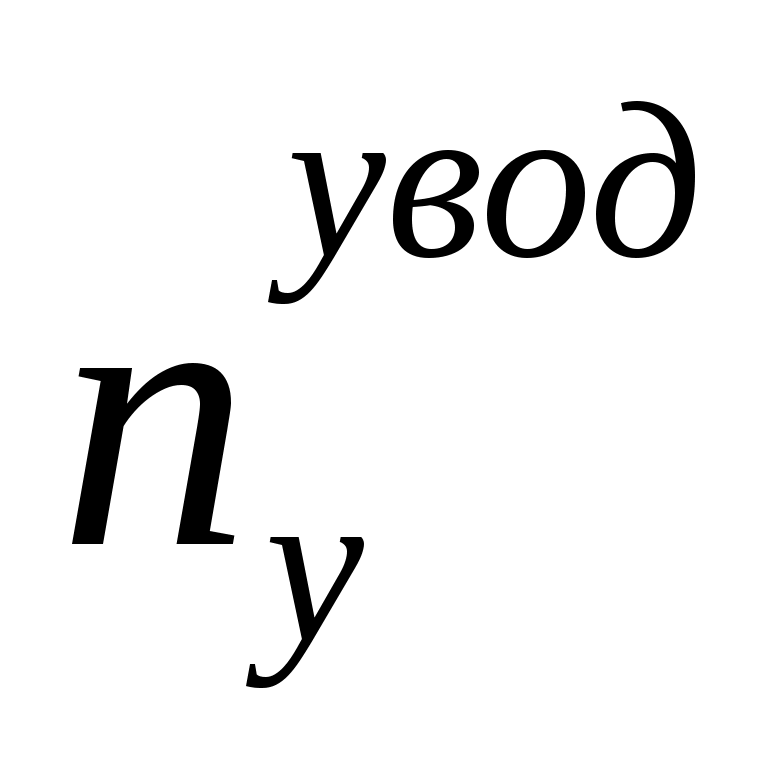 . .

Рис.5.6
Требуется, при заданном известном положении препятствия, определить дальность срабатывания, начиная с которой система увода смогла бы предотвратить столкновение со "стенкой" с перегрузкой 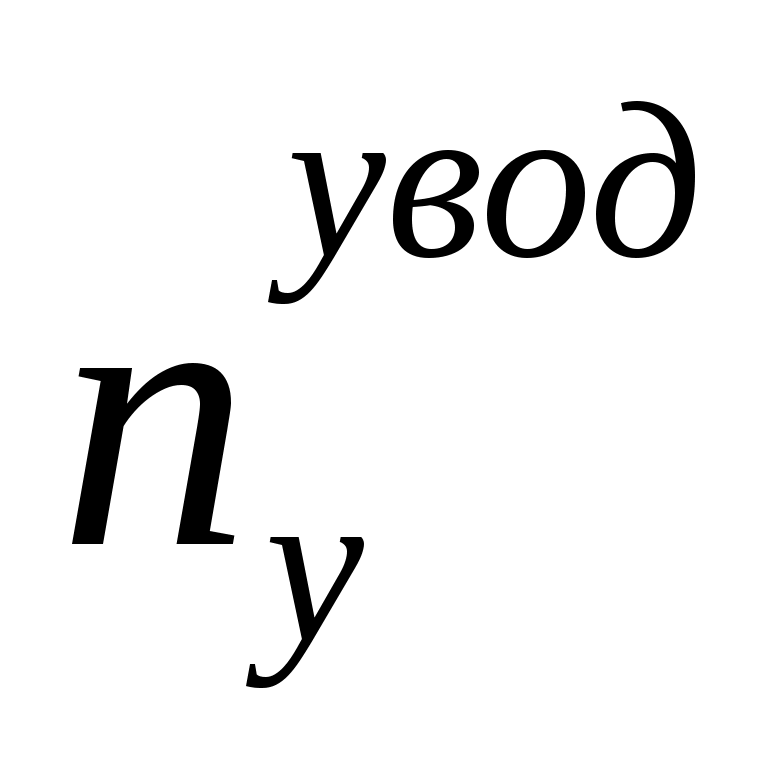 . .
В данном случае, поверхность ограничения представлена уравнением первой степени
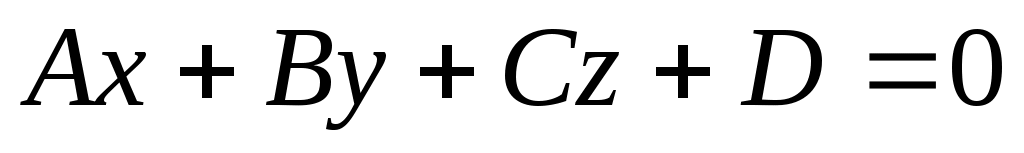 , ,
где A=1, В=0, С=0, D=-3.
В качестве начальных условий принимаются текущие значения углов крена и наклона траектории:
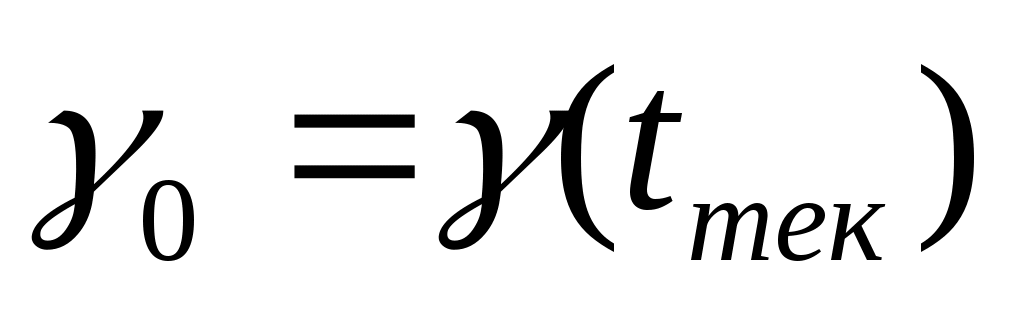 , ,  , ,
Их заданные конечные значения зависят от курсового угла подхода к стенке φ (см. рис.5.7). Под ним будем понимать угол между проекцией вектора скорости самолета на горизонтальную плоскость 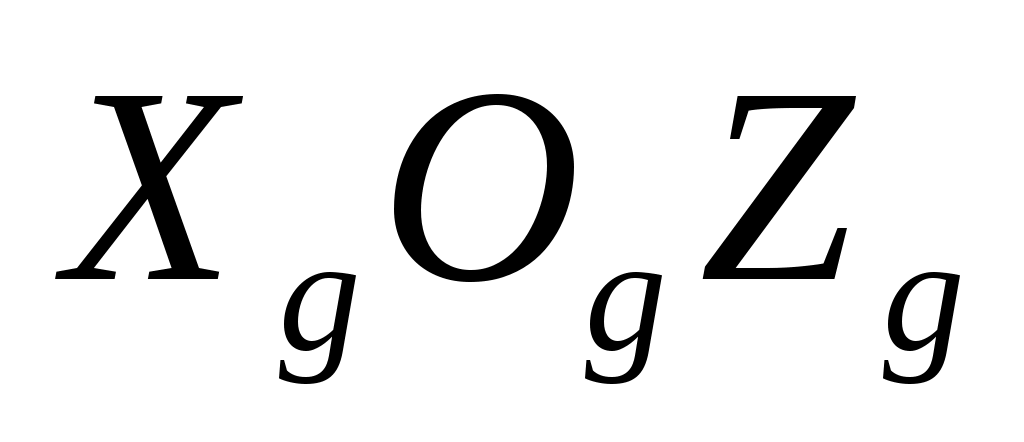 и прямой пересечения стенки с горизонтом L. и прямой пересечения стенки с горизонтом L.
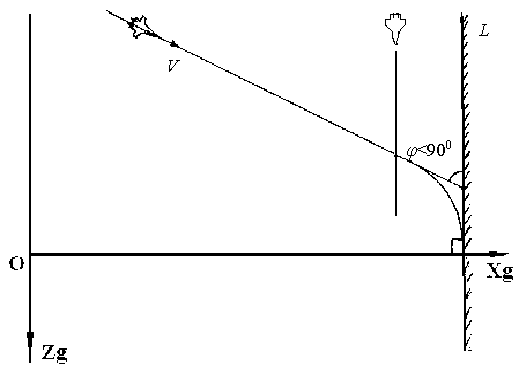
Рис.5.7
Очевидно, что в случае 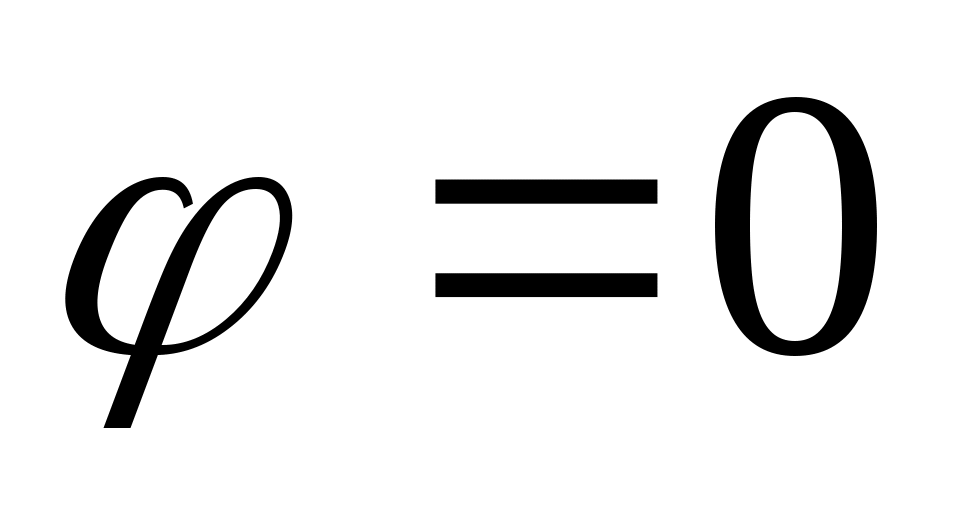 град полет осуществляется параллельно препятствию слева или справа. Следовательно, по причине отсутствия точки Т на поверхности ограничения, получаемой пересечением линии продолжения вектора скорости самолета с поверхностью, алгоритм никогда не вступит в работу. град полет осуществляется параллельно препятствию слева или справа. Следовательно, по причине отсутствия точки Т на поверхности ограничения, получаемой пересечением линии продолжения вектора скорости самолета с поверхностью, алгоритм никогда не вступит в работу.
Когда 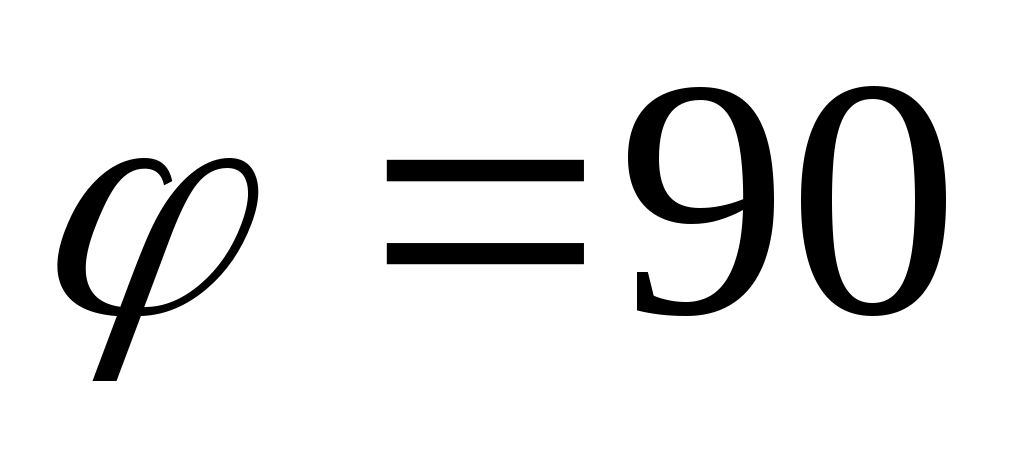 град, траектория полета объекта проходит вдоль нормали к препятствию. Конечные условия, согласно зависимостям (5.9) и (5.11), принимают следующие значения: град, траектория полета объекта проходит вдоль нормали к препятствию. Конечные условия, согласно зависимостям (5.9) и (5.11), принимают следующие значения:
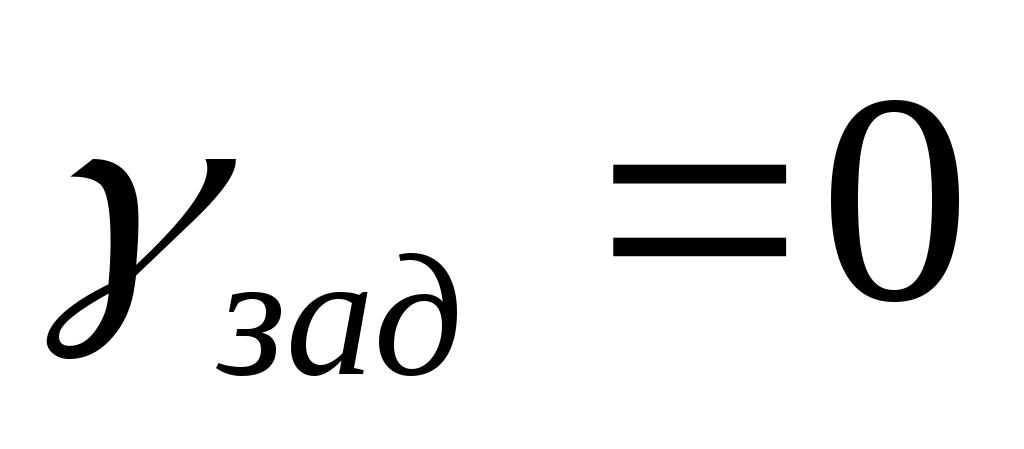 град, град, 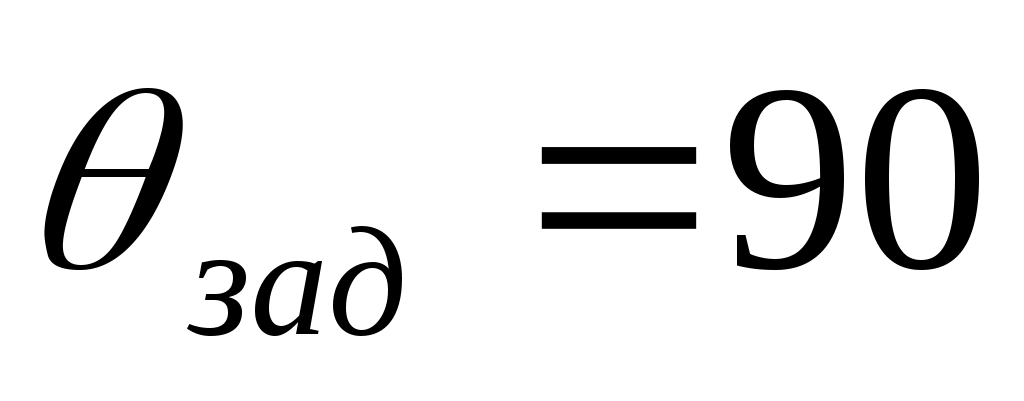 град град
На рис. 5.8 – 5.9 представлены результаты проведенных исследований по оценке работоспособности алгоритма при 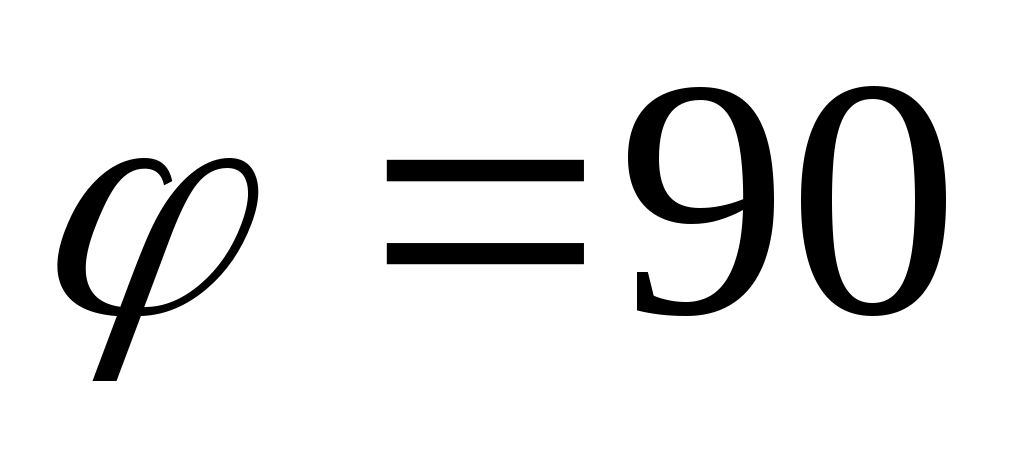 град. Осуществлялась вариация начальных значений угла пикирования и числа М полета. град. Осуществлялась вариация начальных значений угла пикирования и числа М полета.

Рис.5.8
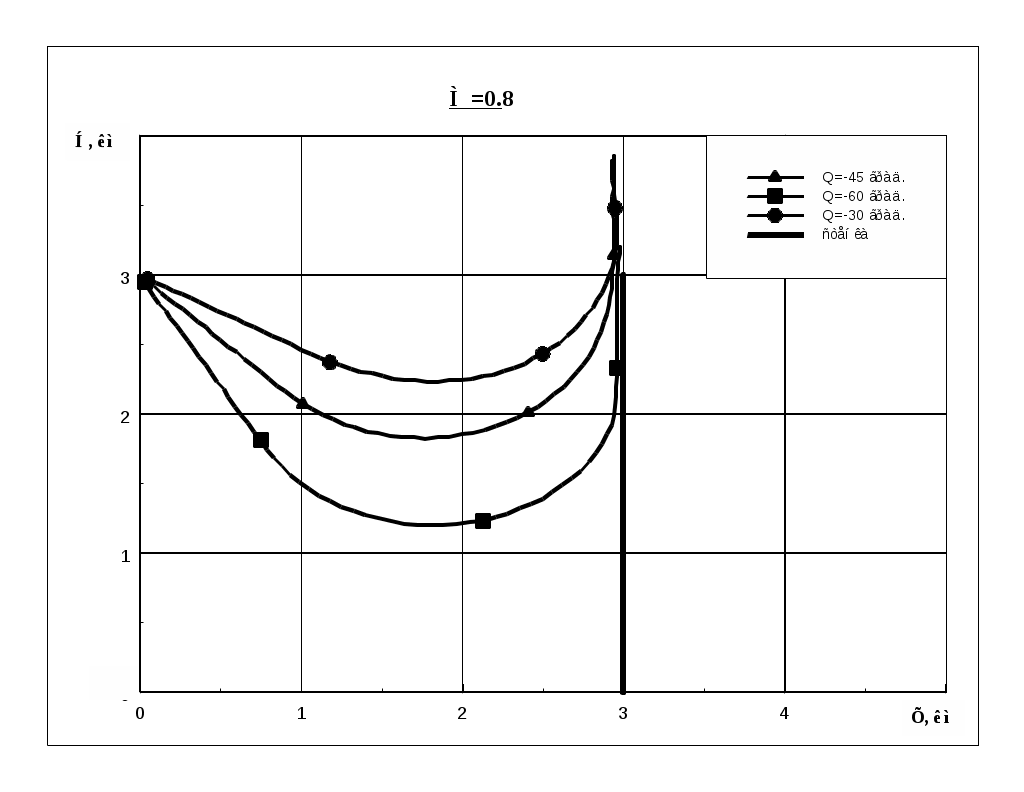
Рис.5.9
Очевидно, что изменение начальных условий в достаточно широком диапазоне не приводит к протыканию объектом поверхности ограничения.
Изменение значения 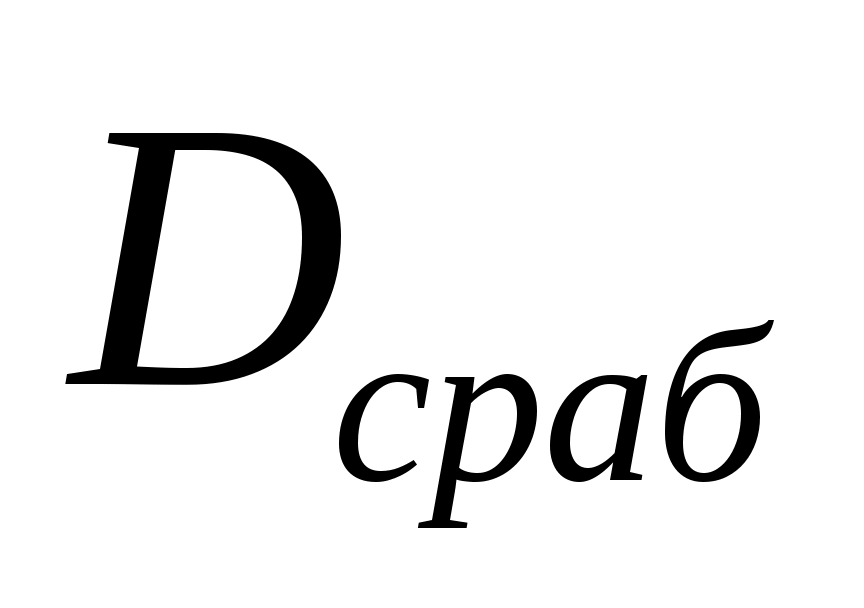 при различных значениях скорости полета имеет характер, близкий к квадратичному (см. рис.5.10). Наличие минимума функции при различных значениях скорости полета имеет характер, близкий к квадратичному (см. рис.5.10). Наличие минимума функции 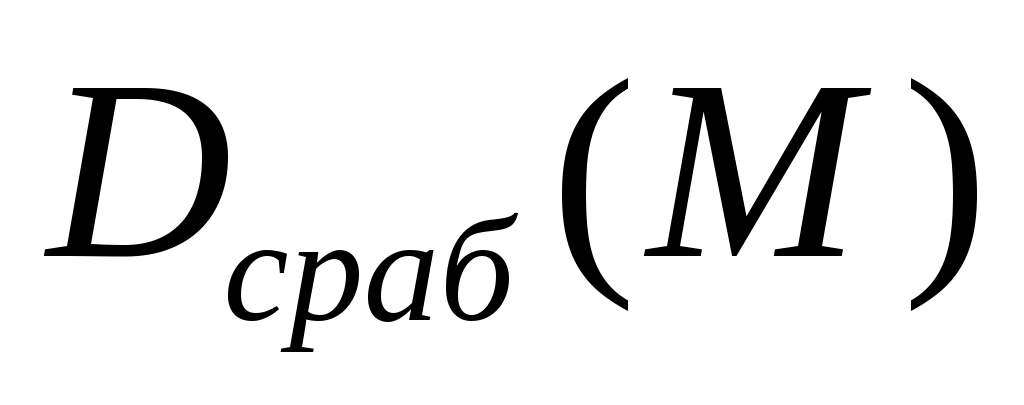 по числу М полета вблизи значения 0.8, можно объяснить возможностью создания на данной скорости полета максимально располагаемой перегрузки увода, равной предельно допустимой перегрузки для самолета. Поэтому на М > 0.8 определяющее влияние на величину дальности срабатывания оказывает увеличение скорости полета. по числу М полета вблизи значения 0.8, можно объяснить возможностью создания на данной скорости полета максимально располагаемой перегрузки увода, равной предельно допустимой перегрузки для самолета. Поэтому на М > 0.8 определяющее влияние на величину дальности срабатывания оказывает увеличение скорости полета.
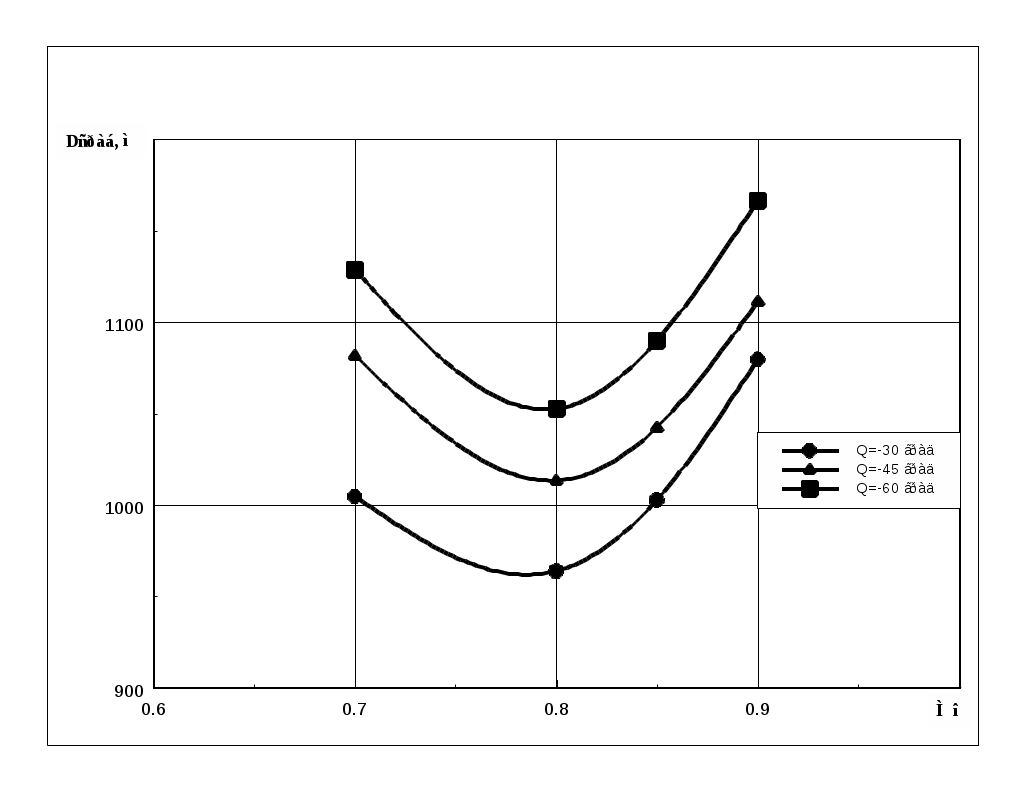
Рис.5.10
В итоге, выполнение задачи увода от препятствия типа "вертикальная стенка" на 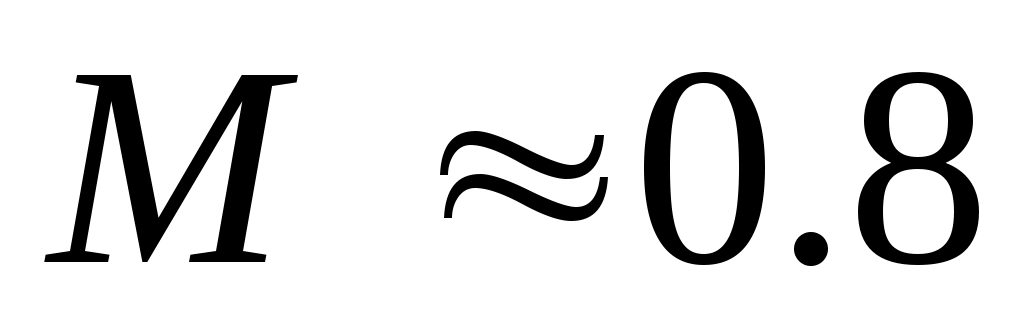 , будет рационально с точки зрения повышения эффективности боевого применения ЛА. Это значит, что алгоритм "позволяя" объекту подойти к поверхности ограничения на меньшее расстояние, обеспечивает сравнительно лучшие условия боевого применения по наземным целям, чем повышается вероятность их поражения. , будет рационально с точки зрения повышения эффективности боевого применения ЛА. Это значит, что алгоритм "позволяя" объекту подойти к поверхности ограничения на меньшее расстояние, обеспечивает сравнительно лучшие условия боевого применения по наземным целям, чем повышается вероятность их поражения.
|
|
|
 Скачать 4.57 Mb.
Скачать 4.57 Mb.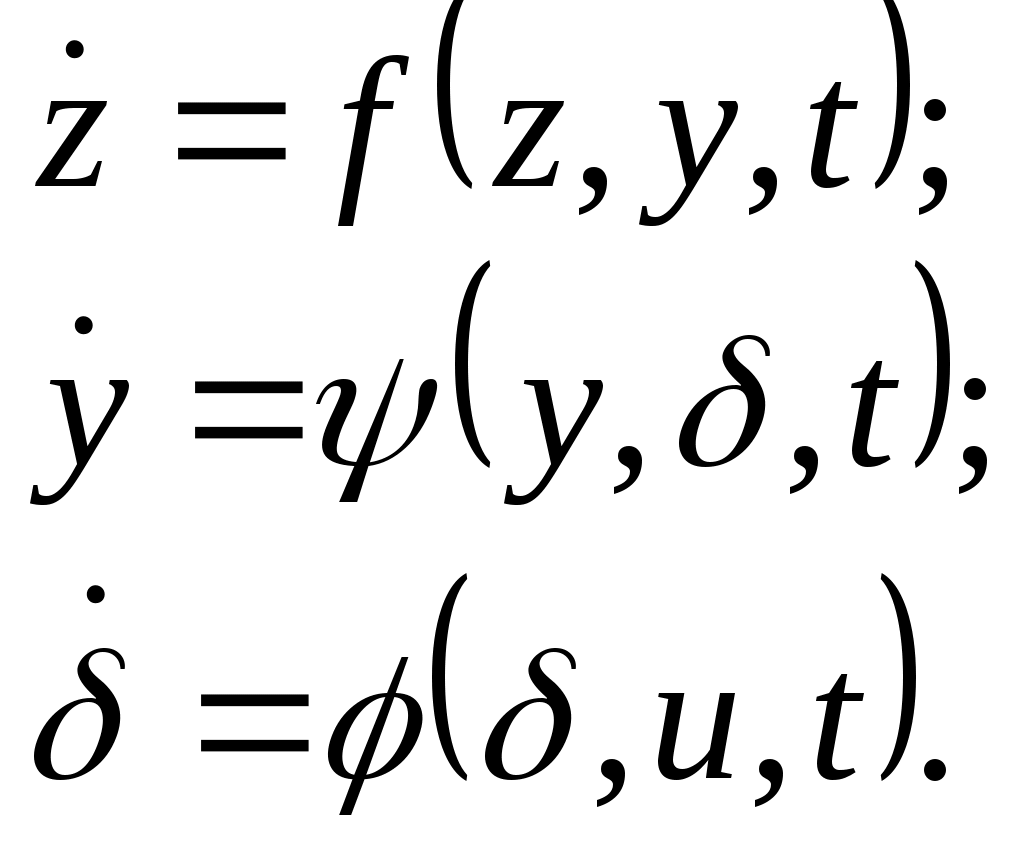 (5.17)
(5.17)