Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения
 Скачать 4.57 Mb.
|
2.3. Доказательство аналогии метода выдерживанияограничений фундаментальному законуравнопеременного движенияРассмотрим задачу выдерживания ограничений для объекта, представленного системой дифференциальных уравнений второго порядка 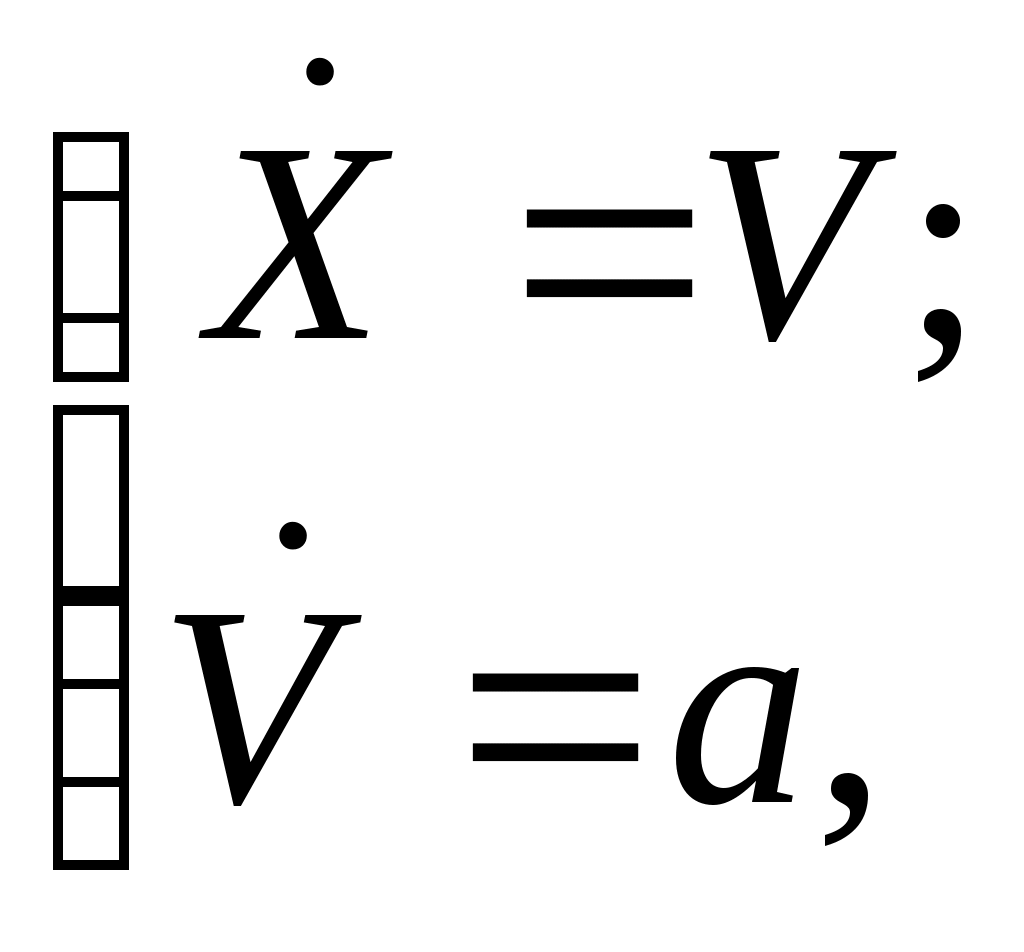 (2.21)Модель (2.21) описывает движение материальной точки в заданном направлении. Здесь X – изменение линейной координаты объекта, V – скорость, a – ускорение. Система (2.21) решается с начальными условиями  .Задачу выдерживания ограничений сформулируем следующим образом. Необходимо включить управление  (2.22)в момент достижения объектом некоторой координаты 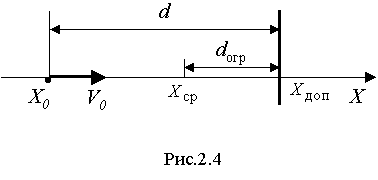 , такой чтобы не произошло превышения ограничения  (см. рис.2.4). Рис.2.4 Эту же задачу можно сформулировать иначе. Для произвольной скорости V найти координату точки  при которой скорость под действием заданного управления  будет сброшена до нуля на уровне  .С учетом известного общего решения системы (2.21) 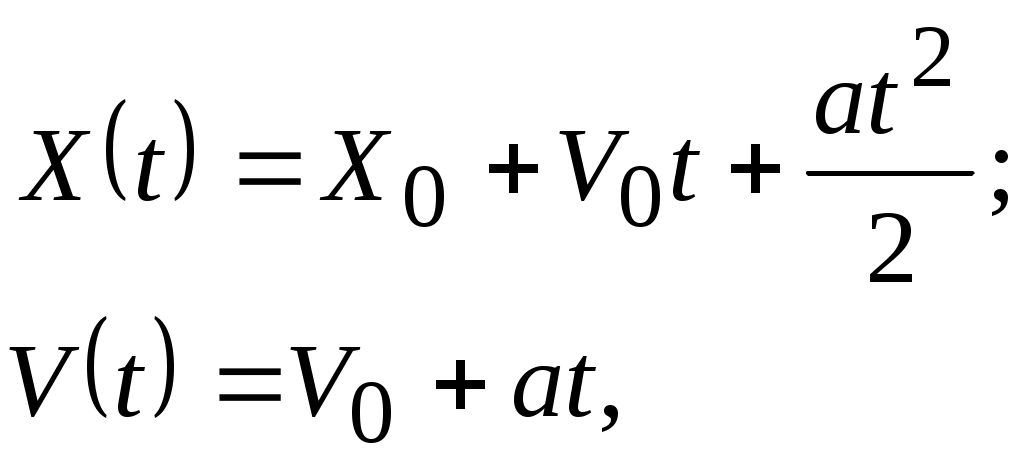 (2.23)для участка торможения  определим значение координаты   , (2.24)где  - время прохождения объектом участка  V - текущая скорость объекта. В итоге имеем два неизвестных  и . Так как по условию , (2.25)то доопределим (2.24) уравнением  . (2.26)Равенство (2.26) получено в результате решения второго уравнения системы (2.21) и записано с учетом (2.25) для интервала  . Выразив из (2.26) и подставив его в (2.24) можно получить выражение для точки включения управления ограничения   . (2.27)Обозначив  , перепишем (2.27) в терминах дальности. В итоге  . (2.28)Нетрудно заметить, что выражение (2.28) полностью совпадает с (2.14). Таким образом, на примере двойного интегрирующего звена получено точное аналитическое решение для расчета длины участка ограничения, что доказывает справедливость выкладок, приведенных для общего случая. Результаты моделирования процесса выдерживания ограничения 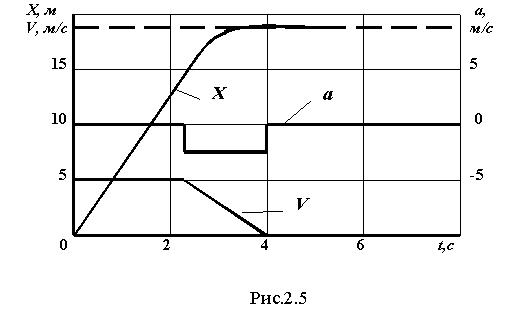 для модели (2.21) представлены на рис.2.5 (случай равномерного движения) и рис.2.6 (равноускоренное движение), и подтверждают работоспособность метода. В обоих случаях при достижении объектом величины  управлению присваивалось значение  .  Рис.2.5 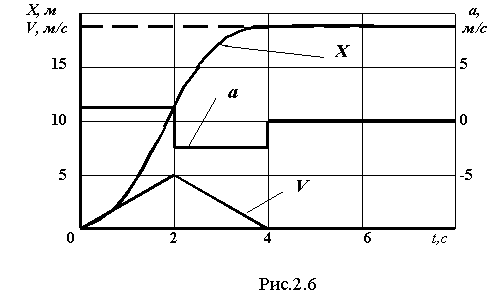 Рис.2.6 В дальнейшем задача управления будет ограничена процессом предотвращения выхода за контролируемый параметр или параметры. Задача стабилизации на уровне допустимого значения параметра рассматриваться не будет. |