|
|
Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения
Рассмотрим произвольный динамический объект, поведение которого описывается некоторой системой n обыкновенных нелинейных дифференциальных уравнений в форме Коши
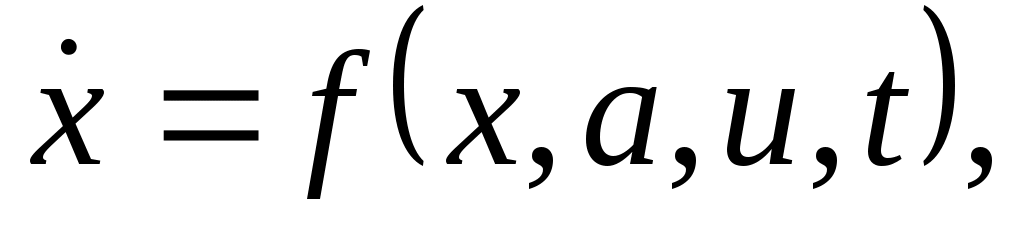 (2.1) (2.1)
где x – n-мерный вектор состояния динамической системы, определенный в пространстве 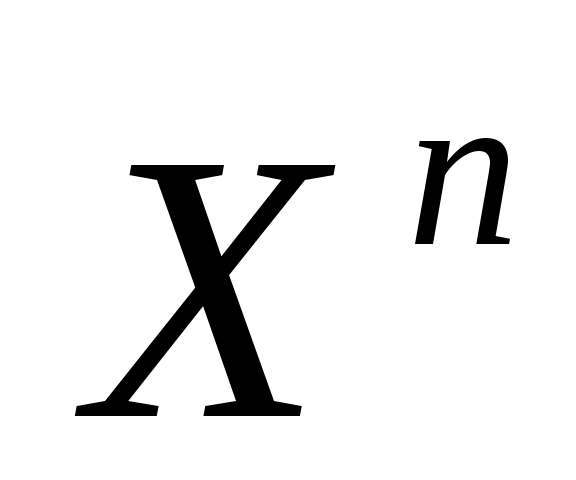 ; a – r-мерный вектор параметров, принимающий значения из множества ; a – r-мерный вектор параметров, принимающий значения из множества 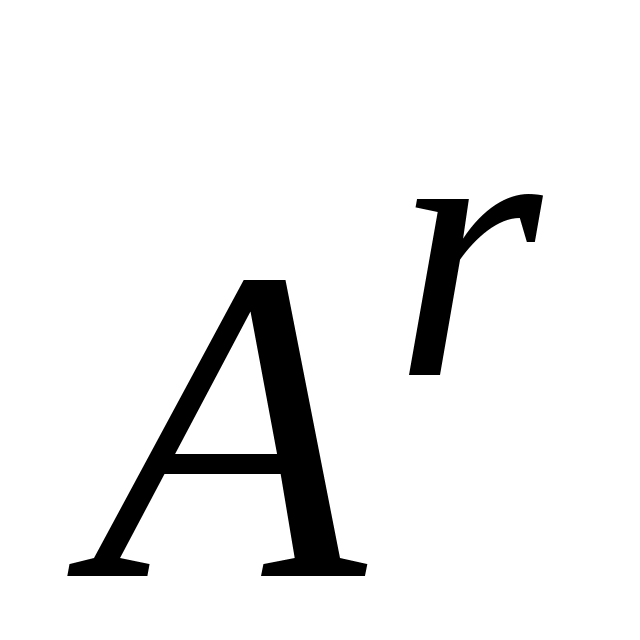 и характеризуемый свойствами объекта и среды; u – m-мерный вектор управляющих воздействий, формируемый системой управления и принадлежащий множеству и характеризуемый свойствами объекта и среды; u – m-мерный вектор управляющих воздействий, формируемый системой управления и принадлежащий множеству 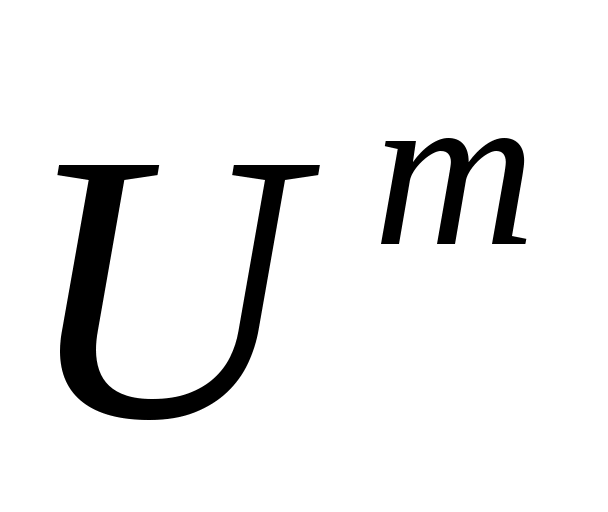 ; t – текущее время, принадлежащее отрезку [t0, tk], на котором определено уравнение (2.1); ; t – текущее время, принадлежащее отрезку [t0, tk], на котором определено уравнение (2.1); 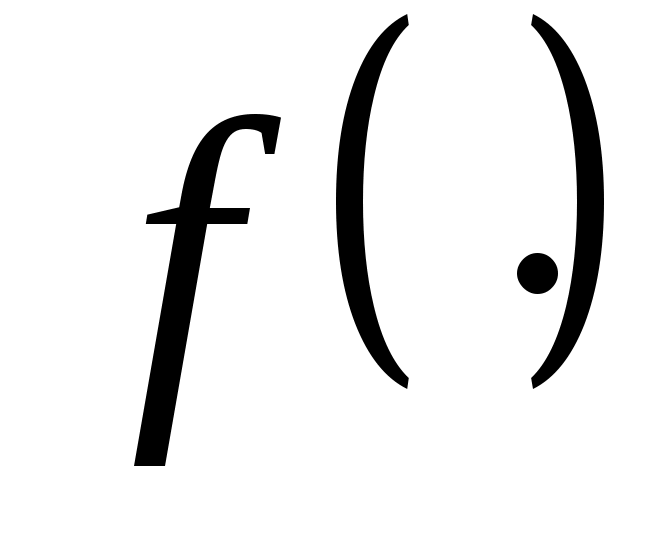 - n-мерная векторная функция указанных аргументов. - n-мерная векторная функция указанных аргументов.
Для системы (2.1) заданы начальные условия
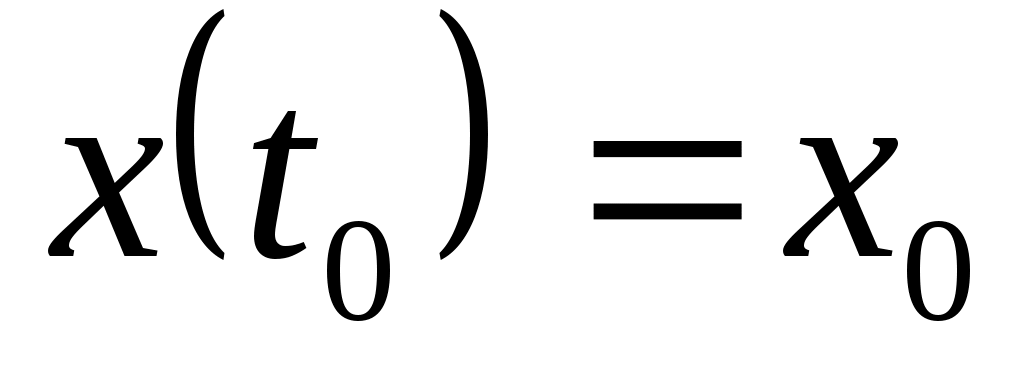
и произвольное управление
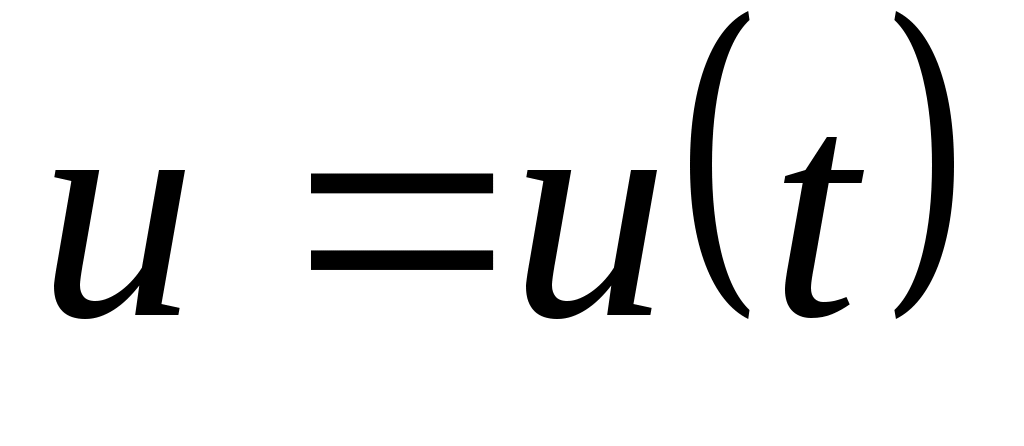 . (2.2) . (2.2)
Пусть в пространстве 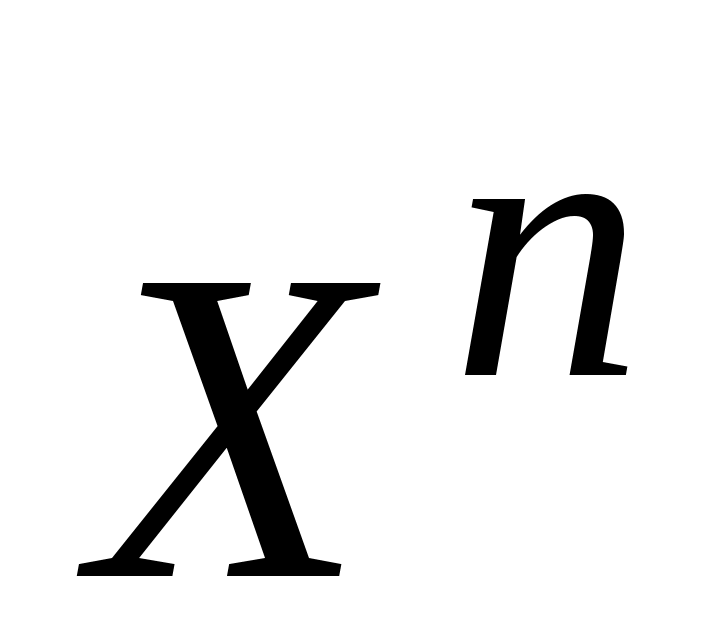 задана некоторая выпуклая по отношению к текущему состоянию динамической системы стационарная поверхность ограничения задана некоторая выпуклая по отношению к текущему состоянию динамической системы стационарная поверхность ограничения
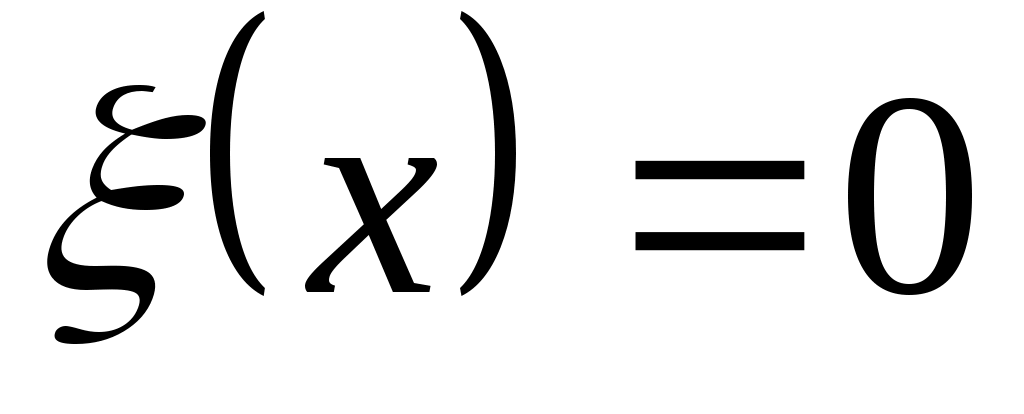 , (2.3) , (2.3)
разделяющая пространство 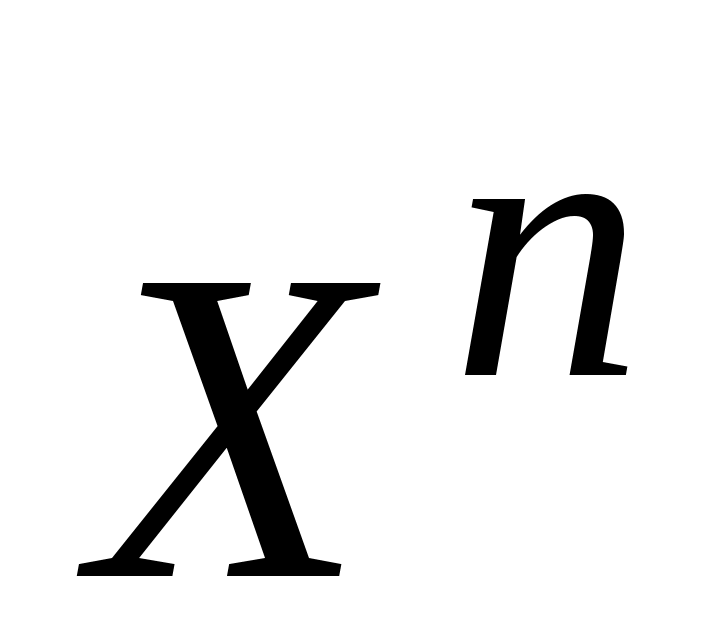 на эксплуатационную и неэксплуатационную область. И известно, что "протыкание" поверхности (2.3) траекторией движения динамической системы x(t) недопустимо из условий ее существования. на эксплуатационную и неэксплуатационную область. И известно, что "протыкание" поверхности (2.3) траекторией движения динамической системы x(t) недопустимо из условий ее существования.
Ставится задача автоматизации выдерживания ограничения, описанного уравнением (2.3) в пространстве состояний 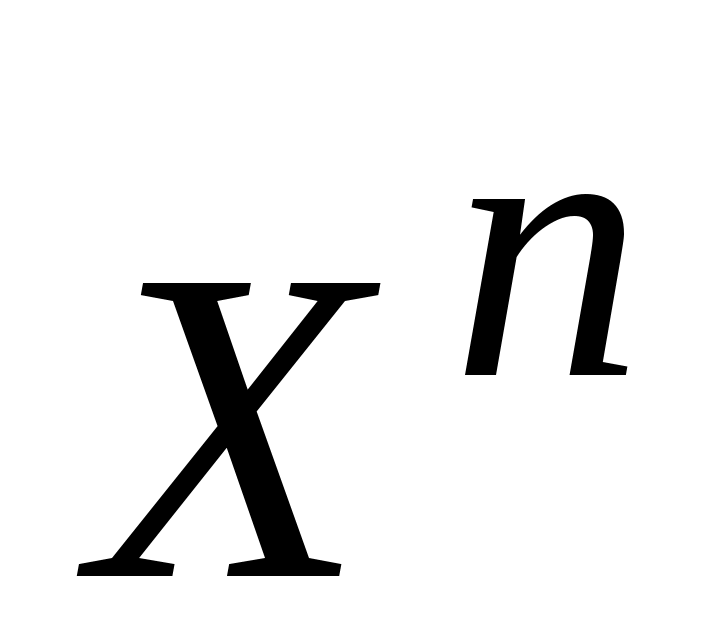 с помощью заранее определенного, релейно срабатываемого управления с помощью заранее определенного, релейно срабатываемого управления  . Для чего необходимо в зависимости от заданного управления ограничения, темпа сближения с поверхностью, а также внутренних параметров самой динамической системы определить момент времени или точку в пространстве состояний . Для чего необходимо в зависимости от заданного управления ограничения, темпа сближения с поверхностью, а также внутренних параметров самой динамической системы определить момент времени или точку в пространстве состояний 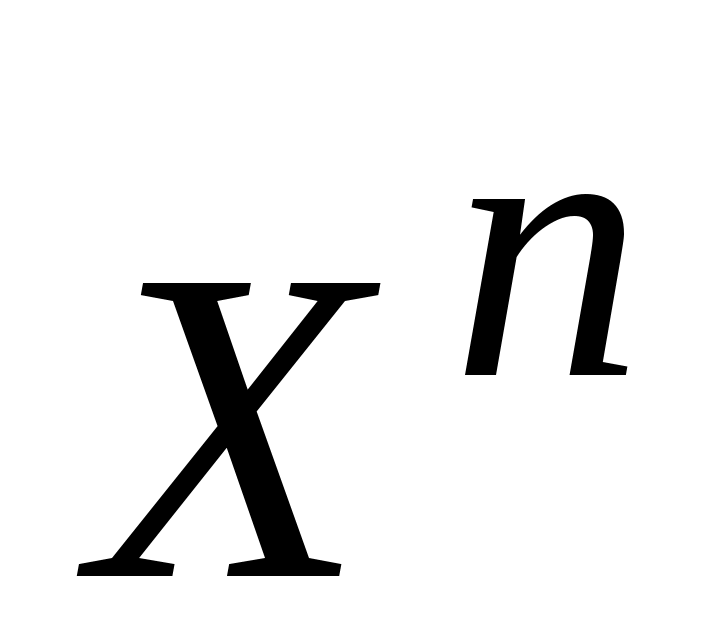 , при котором выбранное управление , при котором выбранное управление 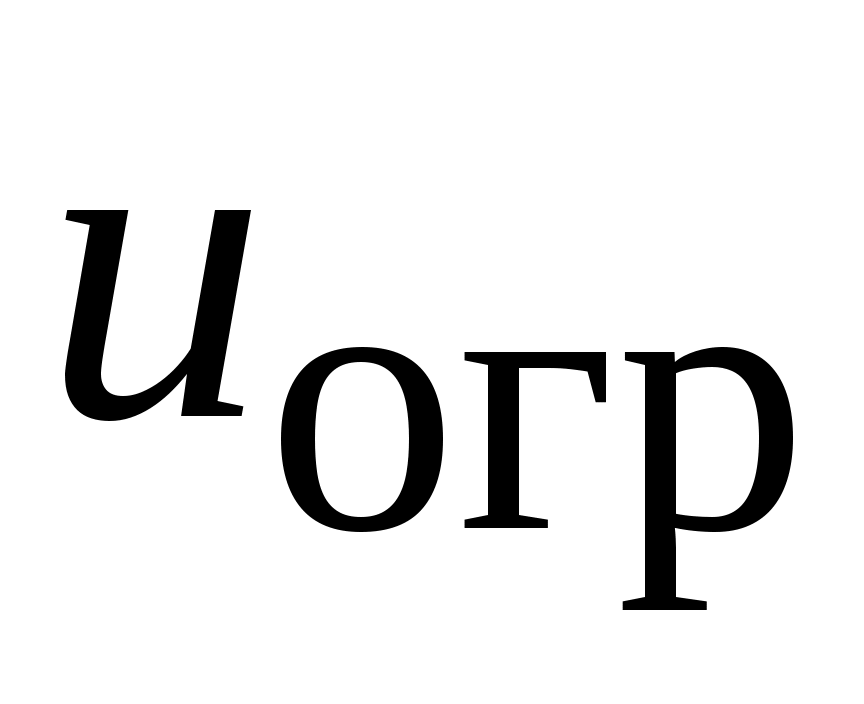 обеспечит касание траекторией движения ДС поверхности ограничения, не протыкая последнюю (см. рис.2.1). обеспечит касание траекторией движения ДС поверхности ограничения, не протыкая последнюю (см. рис.2.1).
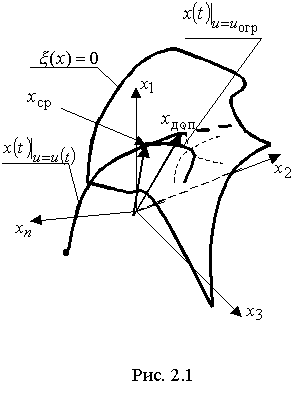
Рис.2.1
На рис.2.1 обозначено 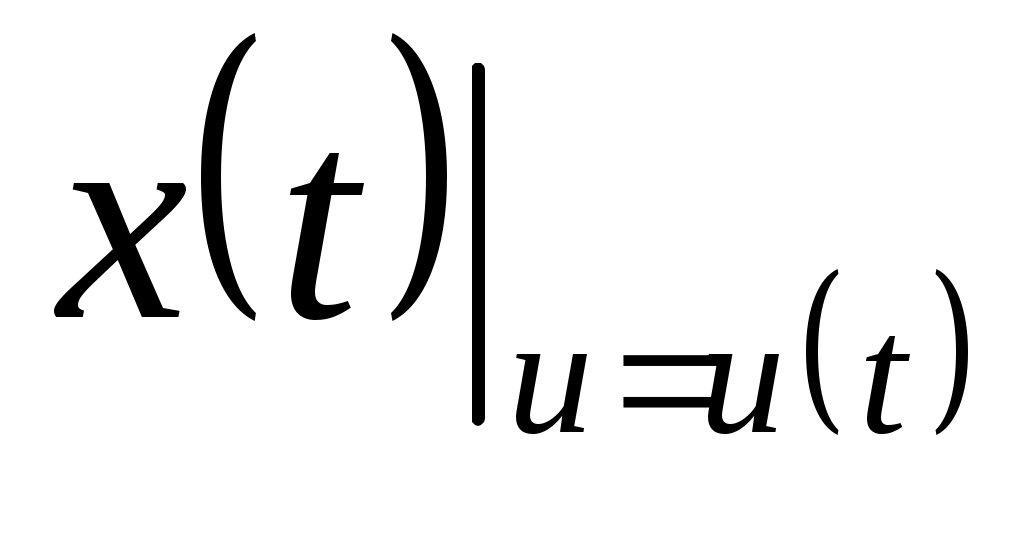 , , 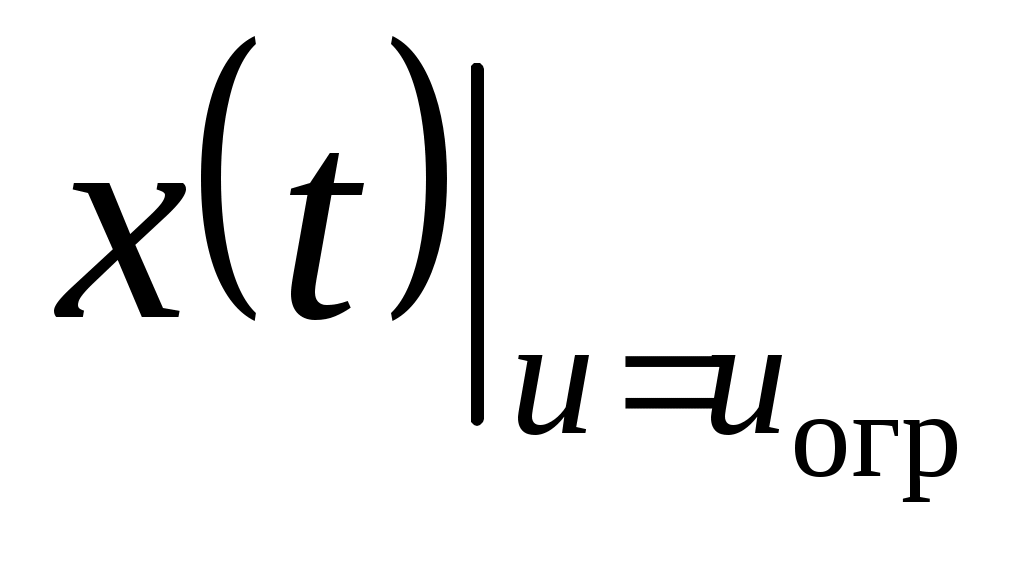 - траектории движения ДС в пространстве - траектории движения ДС в пространстве 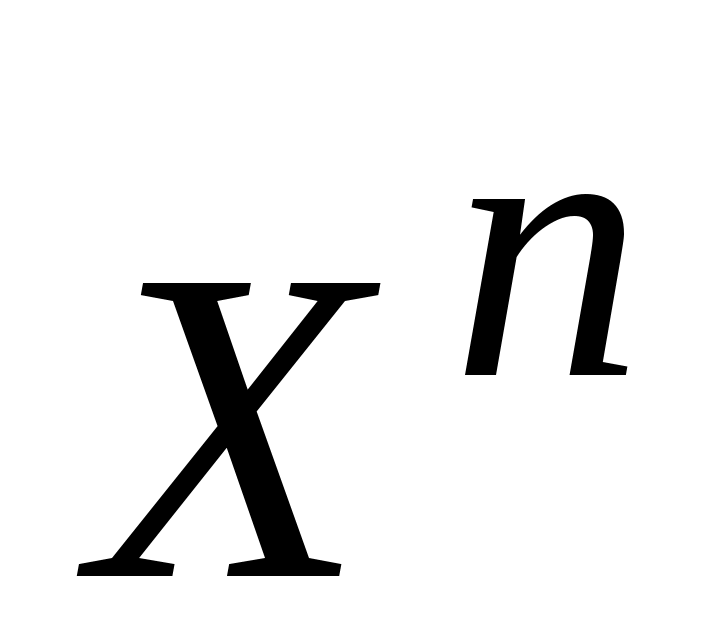 с произвольным управлением и управлением ограничения соответственно; с произвольным управлением и управлением ограничения соответственно; 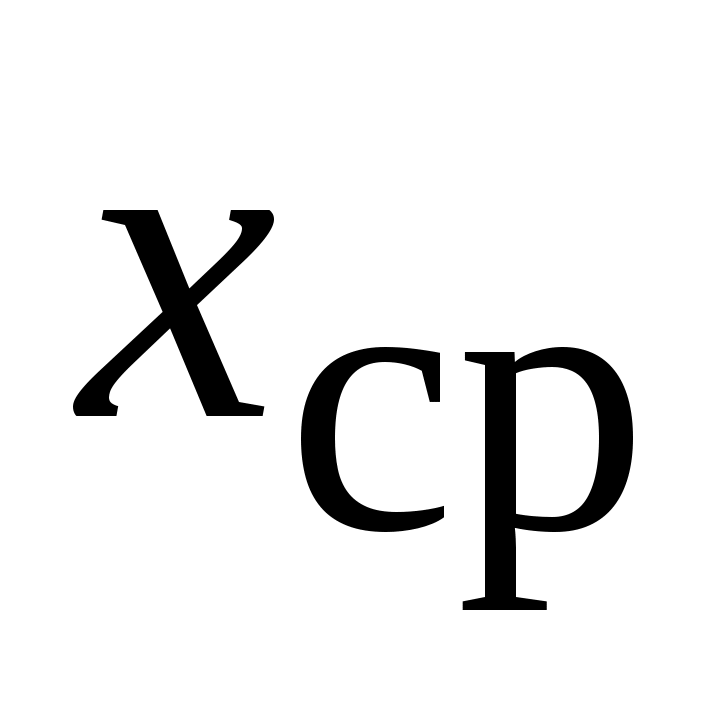 - вектор, характеризуемый точку на траектории движения динамической системы, в которой происходит срабатывание системы ограничения; - вектор, характеризуемый точку на траектории движения динамической системы, в которой происходит срабатывание системы ограничения; 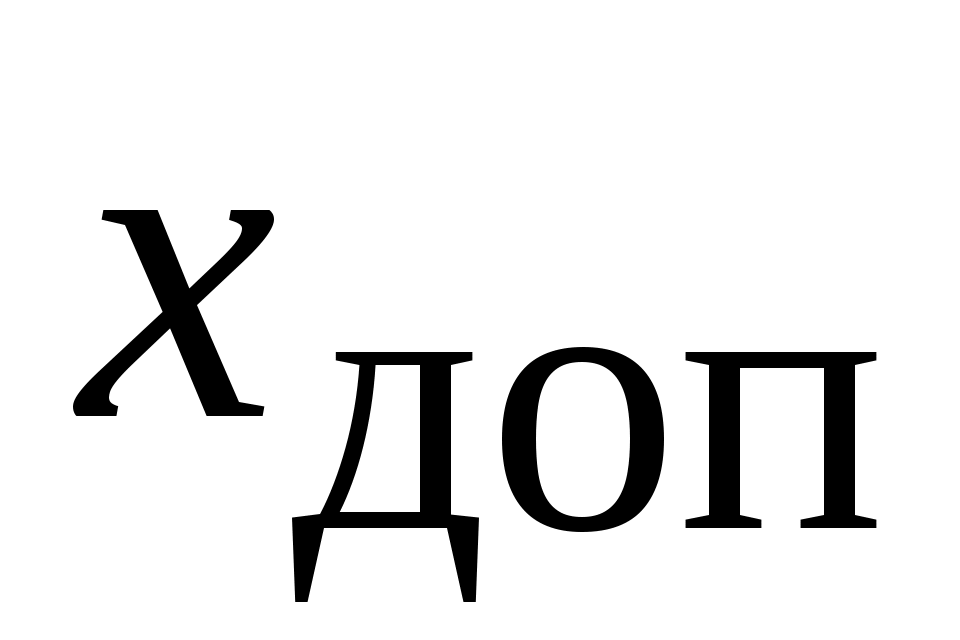 - вектор предельного состояния ДС на траектории - вектор предельного состояния ДС на траектории 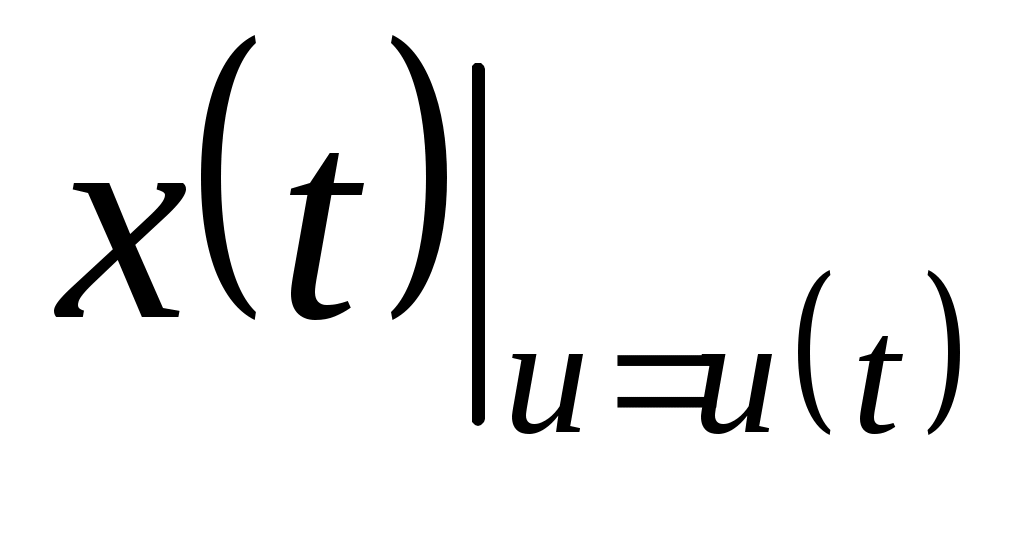 . .
2.2. Общий случай выдерживания ограничения
Рассмотрим некоторым образом предварительно отнормированное пространство 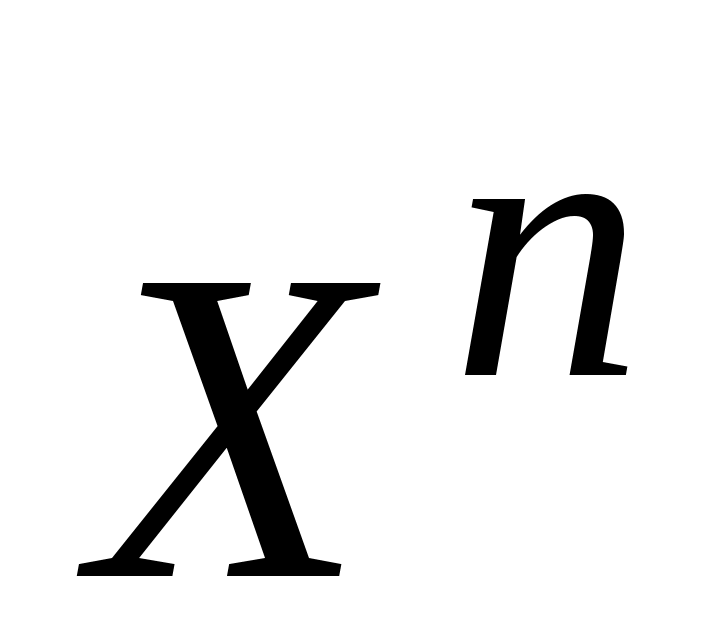 . .
П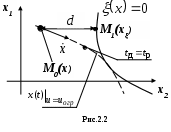
усть в этом пространстве заданы: точка М0(x) с текущими координатами ДС, направление и скорость ее перемещения 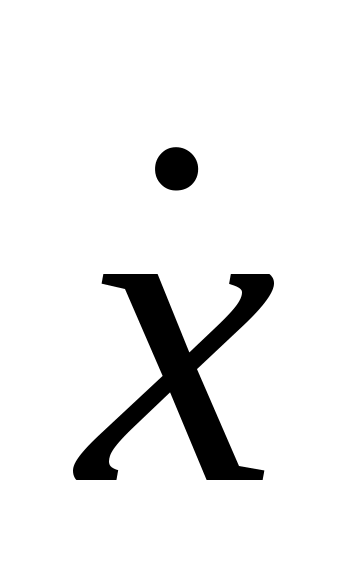 , поверхность ограничения, описанная уравнением (2.3). Геометрическая интерпретация задачи для двухмерного пространства представлена на рис.2.2. , поверхность ограничения, описанная уравнением (2.3). Геометрическая интерпретация задачи для двухмерного пространства представлена на рис.2.2.
Введем понятие дальности d (см. рис.2.2) под которым будем понимать кратчайшее расстояние между точкой М0(x) 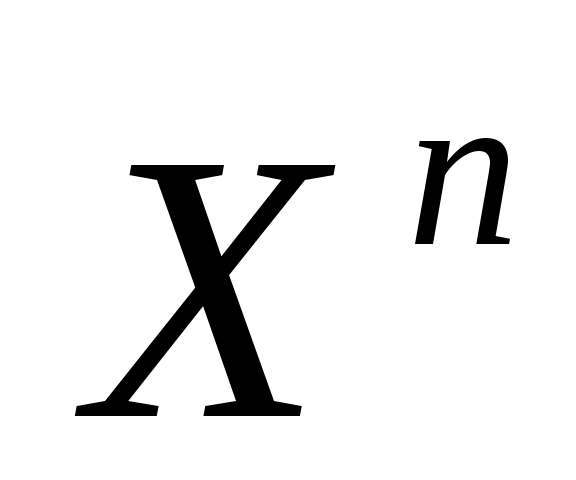 и поверхностью ограничения и поверхностью ограничения 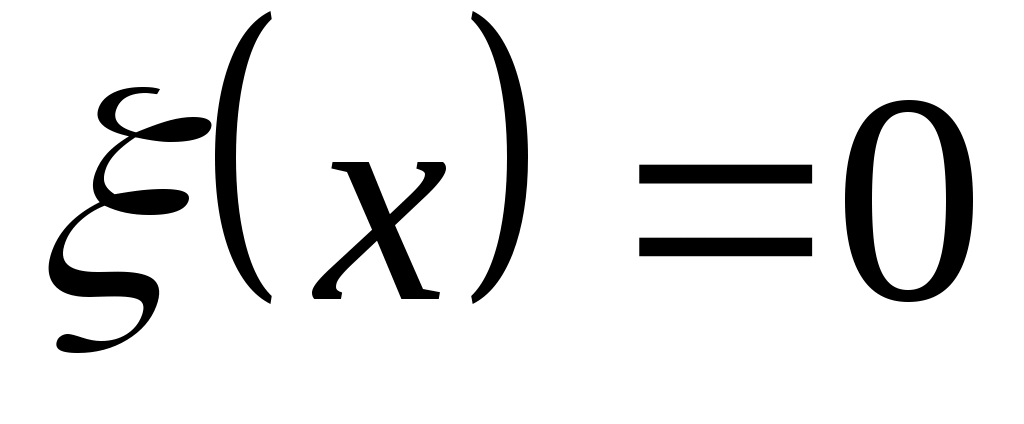 . В общем случае дальность dможет быть определена путем минимизации целевой функции [?] . В общем случае дальность dможет быть определена путем минимизации целевой функции [?]
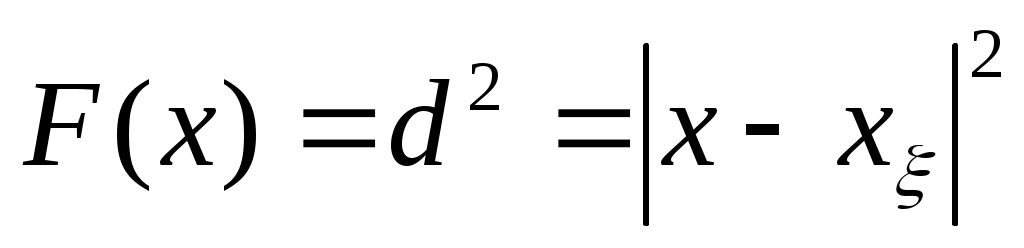 , (2.4) , (2.4)
где 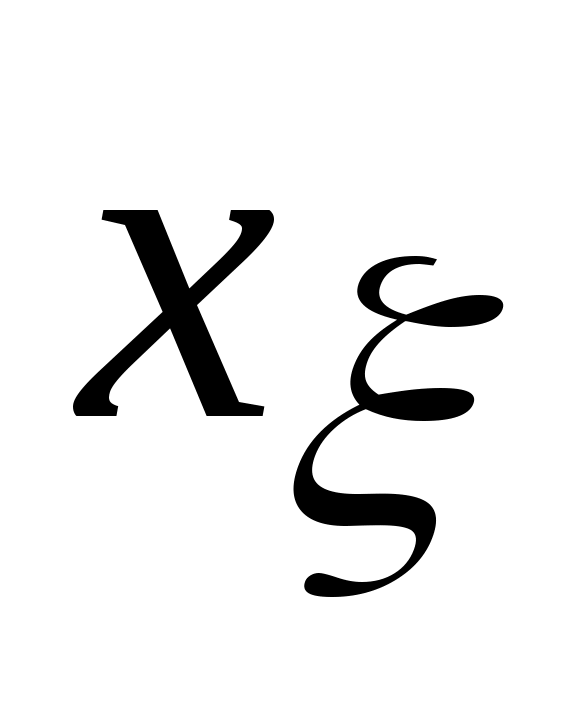 - вектор, координаты которого характеризуют положение произвольной точки М1(x) лежащей на поверхности(x)=0. Координаты вектора - вектор, координаты которого характеризуют положение произвольной точки М1(x) лежащей на поверхности(x)=0. Координаты вектора 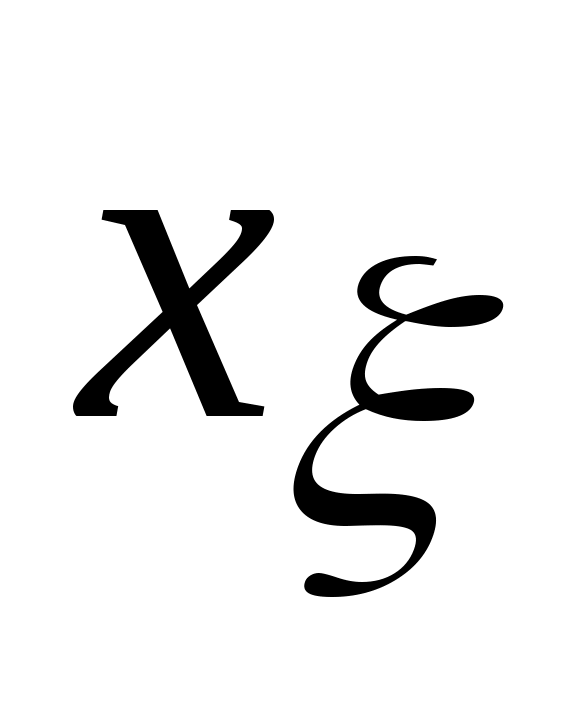 также можно определить, используя уравнение нормали к поверхности ограничения, проходящей через точку М0(x), на основании очевидного факта, что линия, содержащая кратчайшее расстояние от точки М0(x) до поверхности ограничения совпадает с нормалью к поверхности ограничения в точке М1(x). также можно определить, используя уравнение нормали к поверхности ограничения, проходящей через точку М0(x), на основании очевидного факта, что линия, содержащая кратчайшее расстояние от точки М0(x) до поверхности ограничения совпадает с нормалью к поверхности ограничения в точке М1(x).
Следует отметить, что любое смещение в пространстве 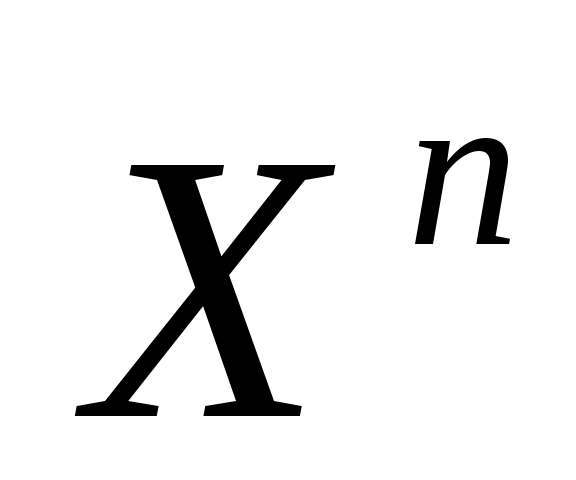 точки М0(x) вызывает соответствующее смещение по поверхности ограничения точки М1(x), удовлетворяющей min точки М0(x) вызывает соответствующее смещение по поверхности ограничения точки М1(x), удовлетворяющей min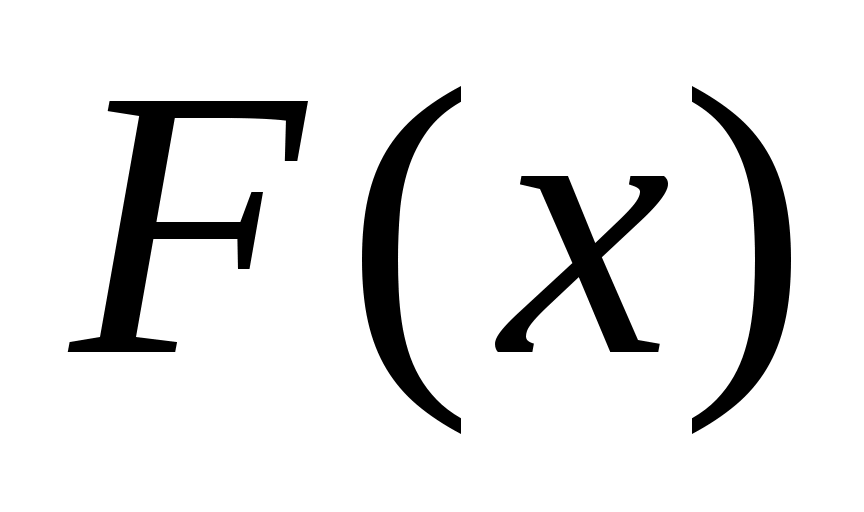 . Поэтому имеет место следующая формальная зависимость . Поэтому имеет место следующая формальная зависимость
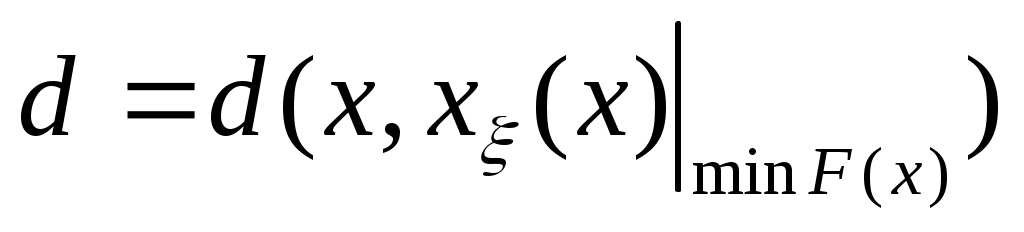 . (2.5) . (2.5)
В дальнейшем индекс 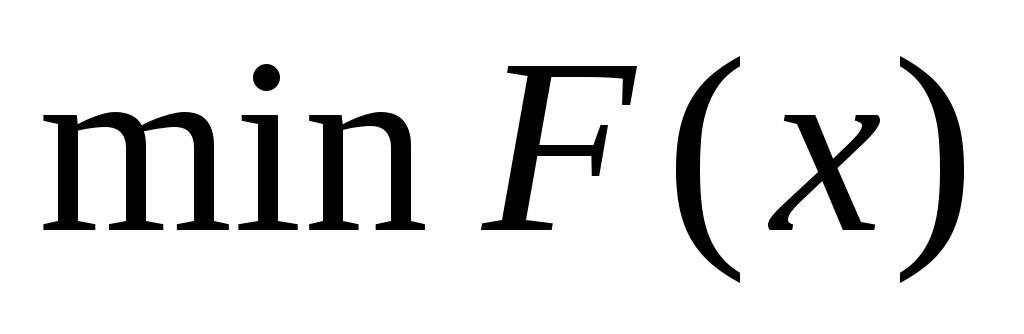 будет опущен. будет опущен.
Рассмотрим в терминах дальности процедуру выхода на границу 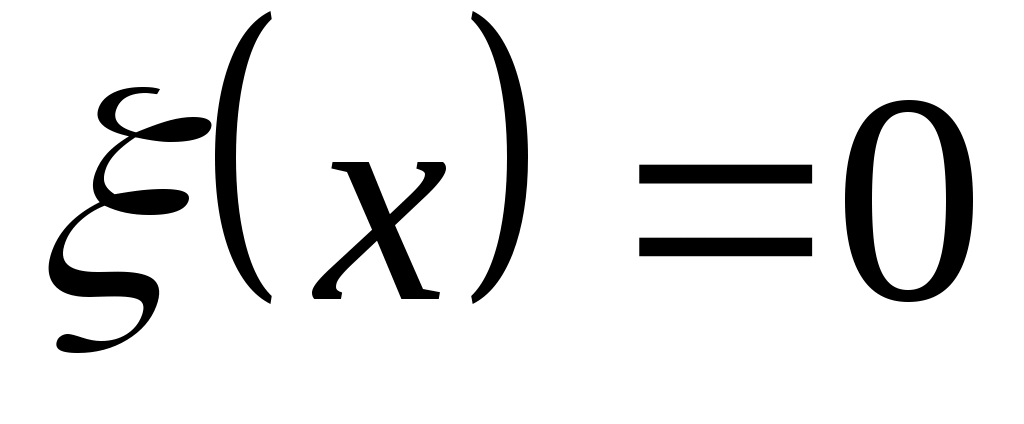 , с учетом ее непротыкания. Для этого проанализируем два характерных интервала времени. Первый интервал представляет собой время достижения ДС поверхности ограничения. Обозначим его - , с учетом ее непротыкания. Для этого проанализируем два характерных интервала времени. Первый интервал представляет собой время достижения ДС поверхности ограничения. Обозначим его - 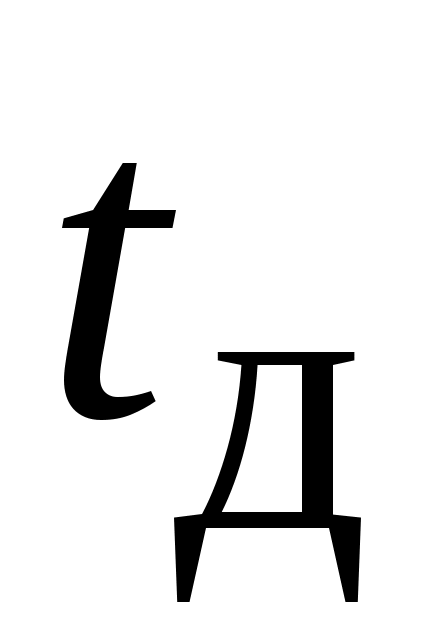 . Второй интервал – располагаемое время . Второй интервал – располагаемое время 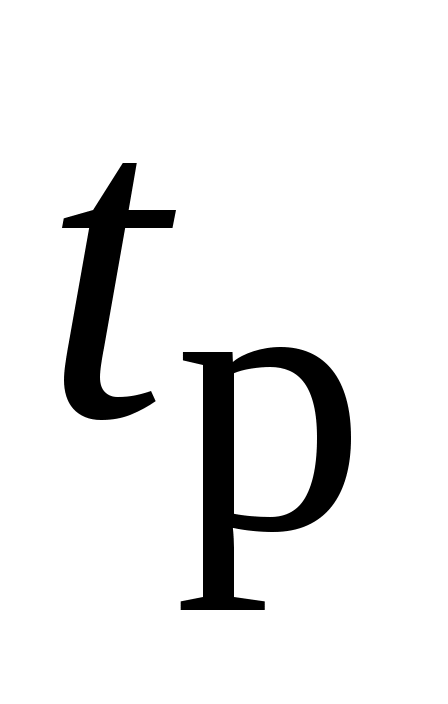 , за которое можно погасить темп сближения с поверхностью ограничения до нуля. Оба временных интервала определяются в предположении, что для ДС реализуется управление ограничения , за которое можно погасить темп сближения с поверхностью ограничения до нуля. Оба временных интервала определяются в предположении, что для ДС реализуется управление ограничения
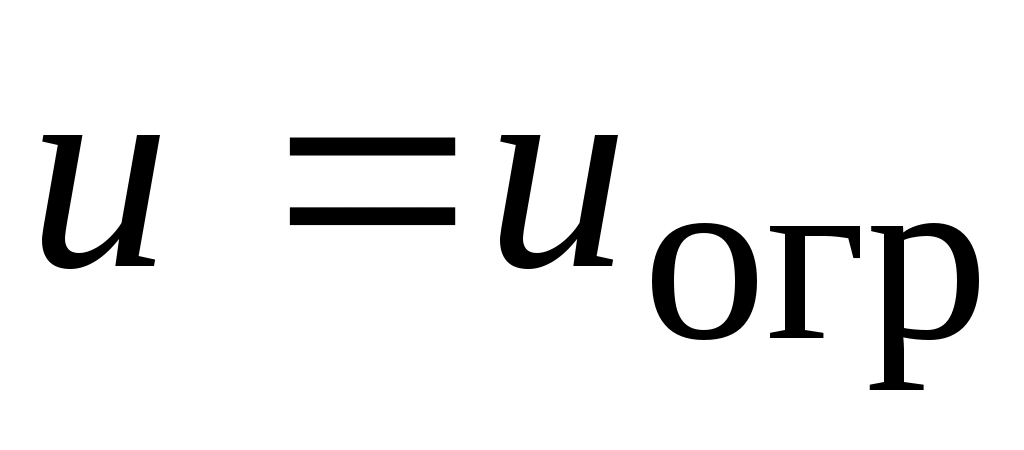 . (2.6) . (2.6)
Естественно предположить, что при достижении равенства
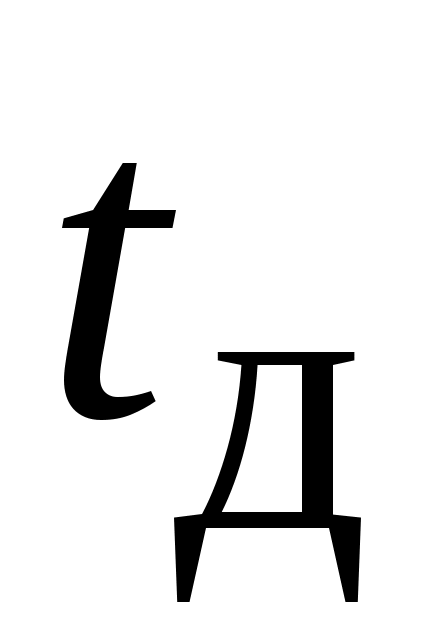 = =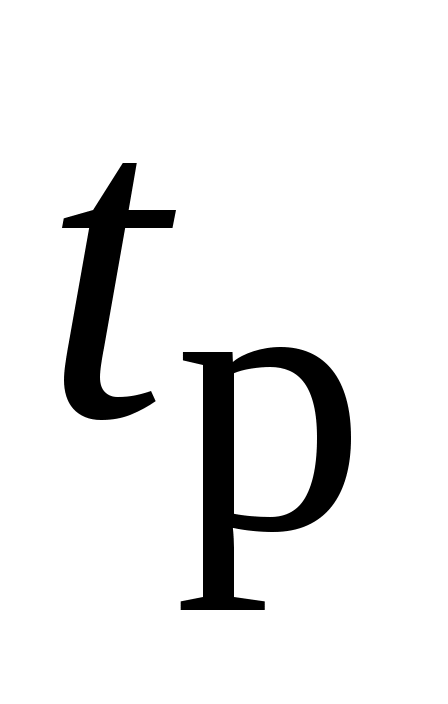 (2.7) (2.7)
траектория движения ДС с управлением (2.6), включенным в момент времени (2.7), лишь коснется поверхности ограничения (см. рис.2.2).
Выразим величины 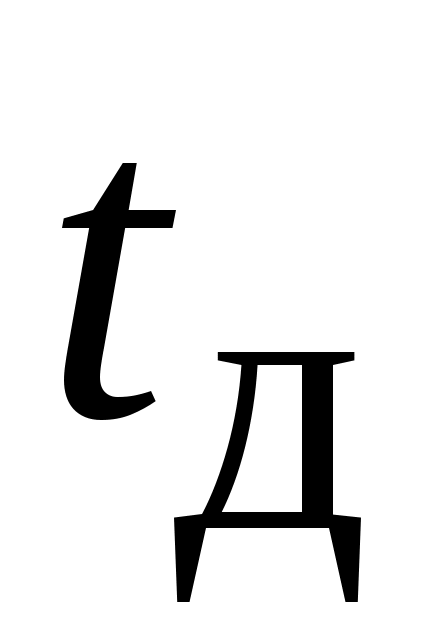 и и 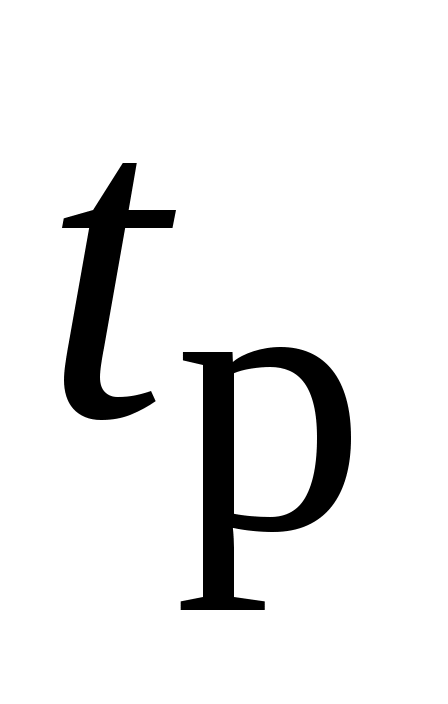 через дальность d и ее производные в предположении, что функция (2.4) определена и дифференцируема на рассматриваемом временном интервале. Тогда время достижения ДС поверхности ограничения будет равно отношению через дальность d и ее производные в предположении, что функция (2.4) определена и дифференцируема на рассматриваемом временном интервале. Тогда время достижения ДС поверхности ограничения будет равно отношению
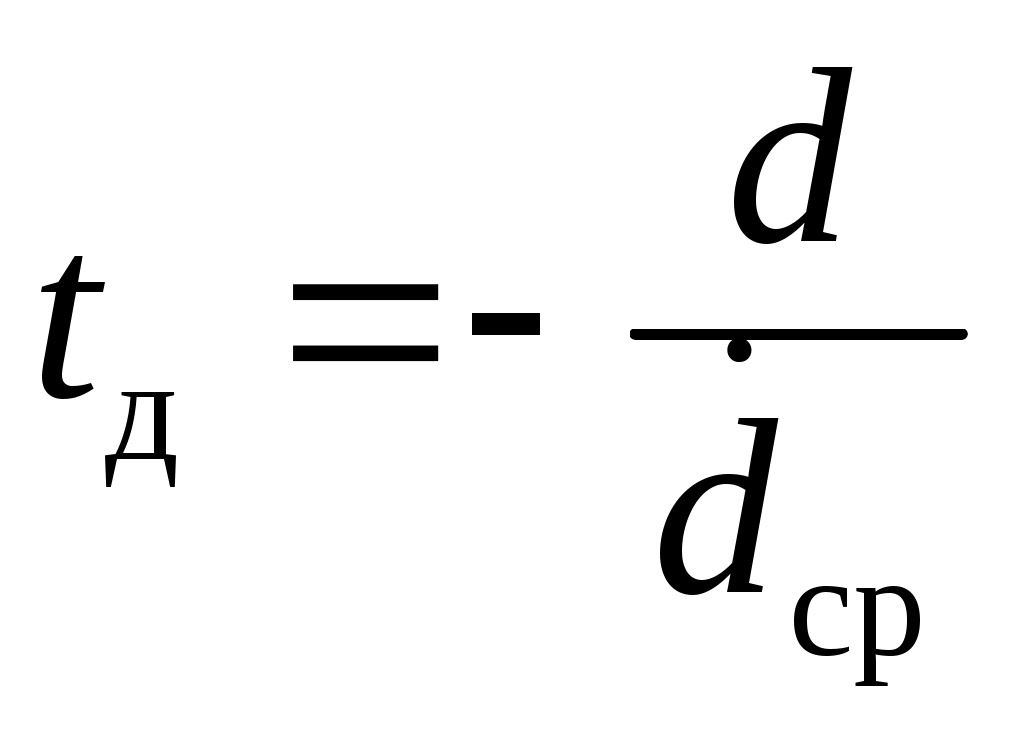 , (2.8) , (2.8)
где 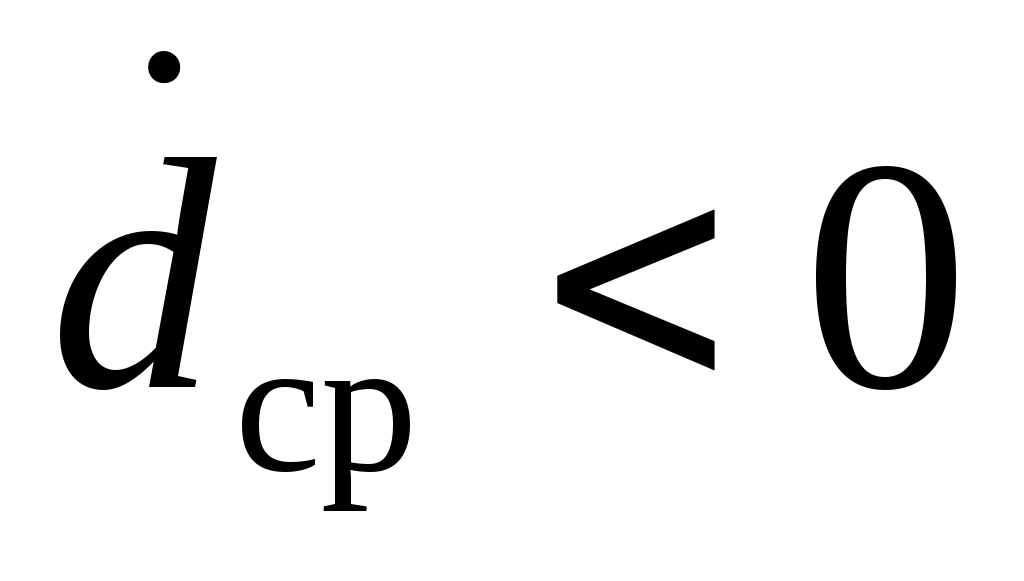 - средняя скорость сближения точки М0(x) с поверхностью ограничения - средняя скорость сближения точки М0(x) с поверхностью ограничения 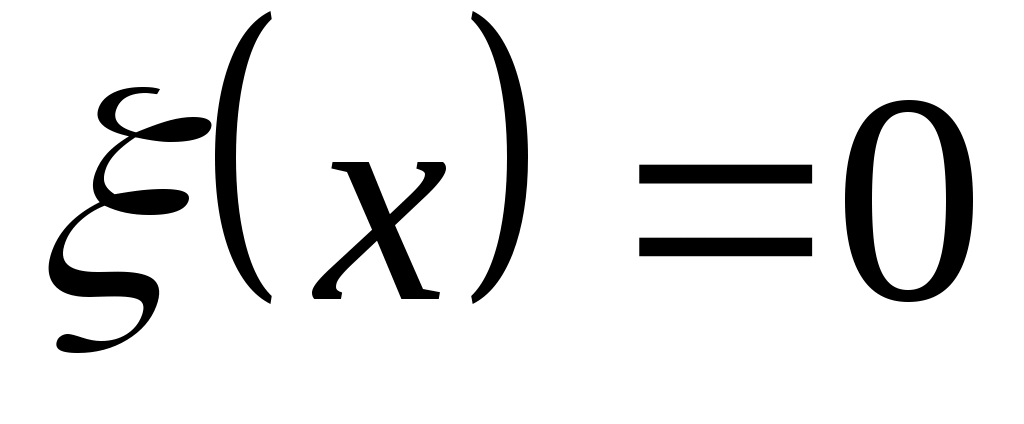 . .
Задавшись условием, что
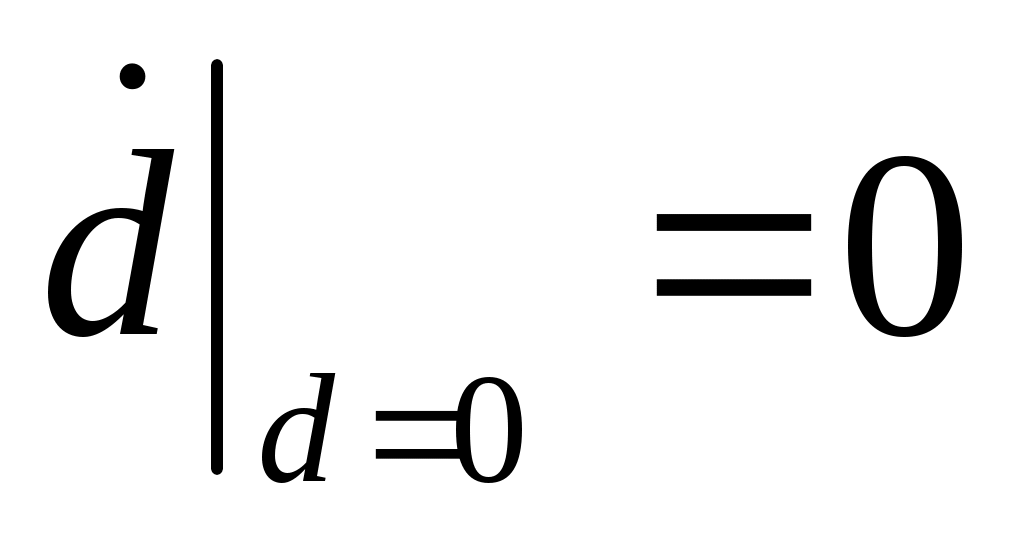 (2.9) (2.9)
и сделав допущение о линейности сброса скорости от текущего значения 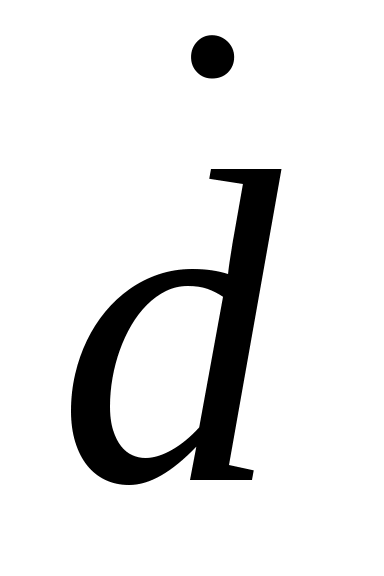 до нуля, обеспечив до нуля, обеспечив 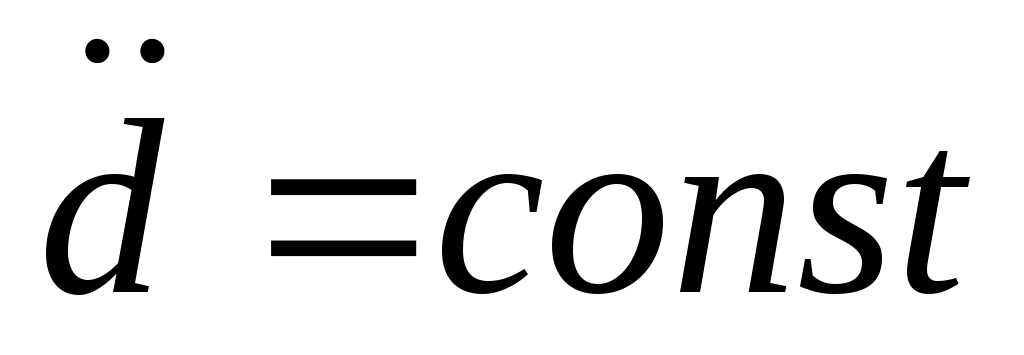 , можно показать, что , можно показать, что
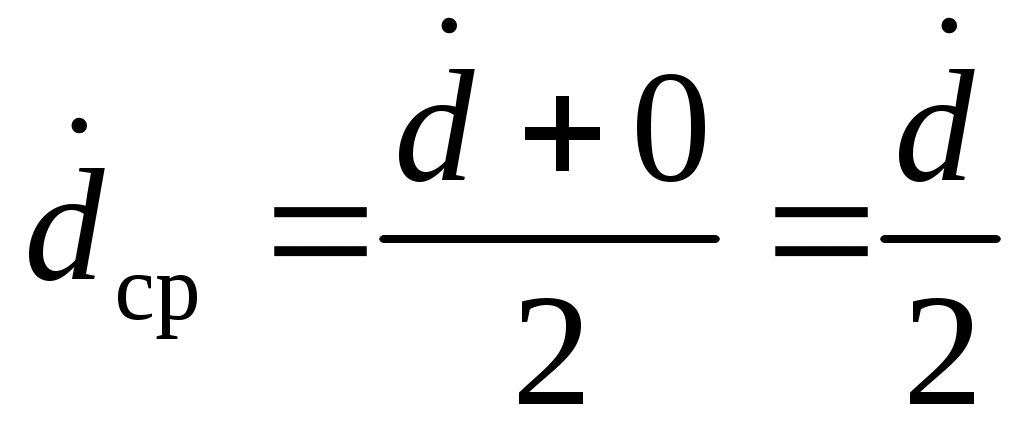 . (2.10) . (2.10)
Подставив (2.10) в (2.8), для времени достижения 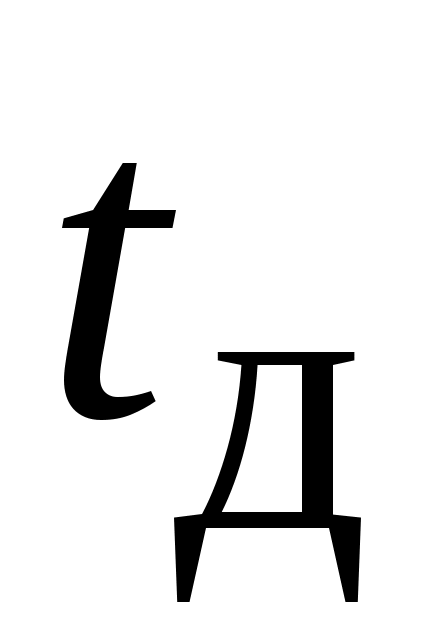 , имеем следующую зависимость , имеем следующую зависимость
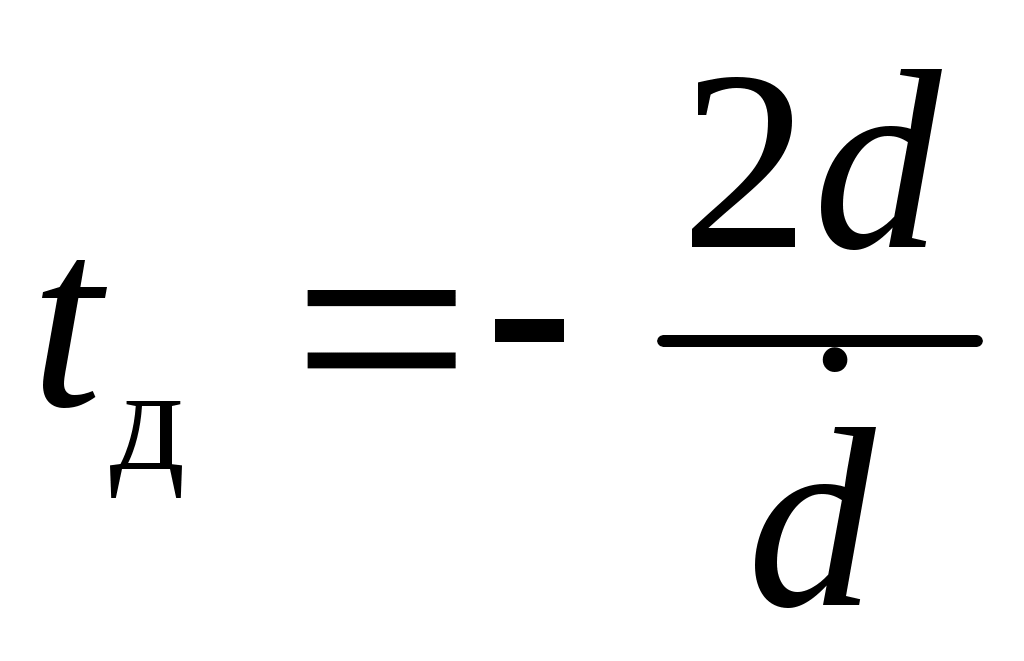 . (2.11) . (2.11)
По аналогии с выражением (2.8), в пространстве производных более высокого порядка располагаемое время 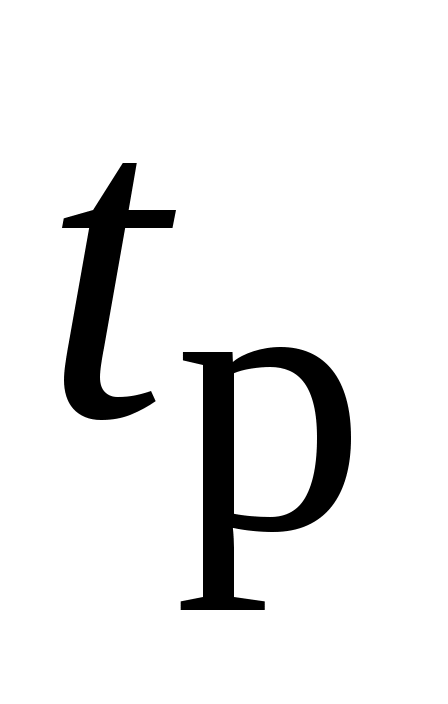 , в соответствии с ее физическим смыслом, определяется выражением , в соответствии с ее физическим смыслом, определяется выражением
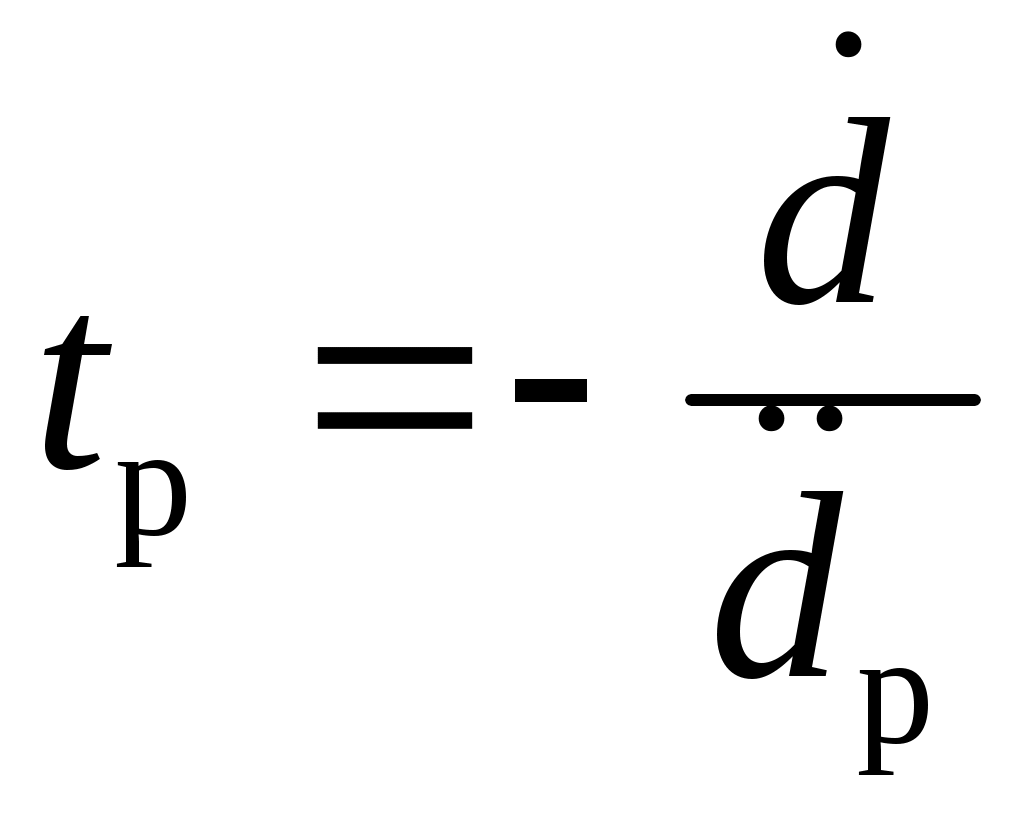 . (2.12) . (2.12)
Здесь 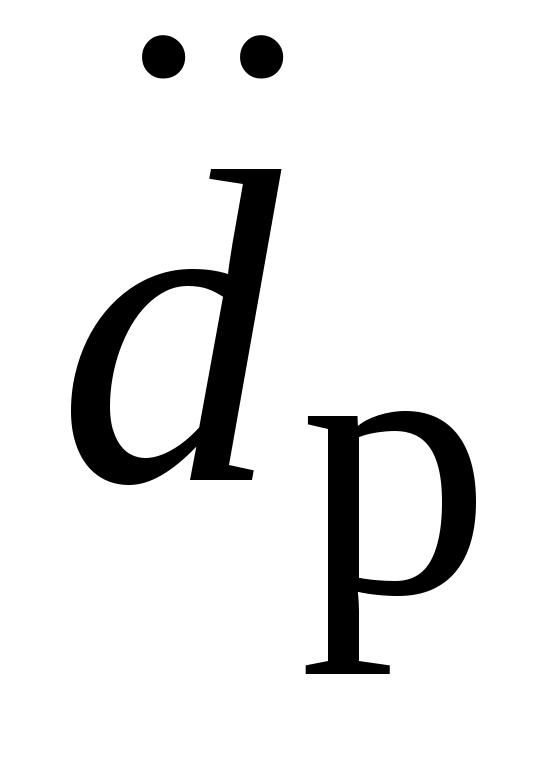 - располагаемое ускорение торможения динамической системы под действием управления ограничения (2.6). - располагаемое ускорение торможения динамической системы под действием управления ограничения (2.6).
Следует отметить, что для корректного решения задачи выдерживания ограничений в данной постановке, также как и для времени достижения, необходимо обеспечить
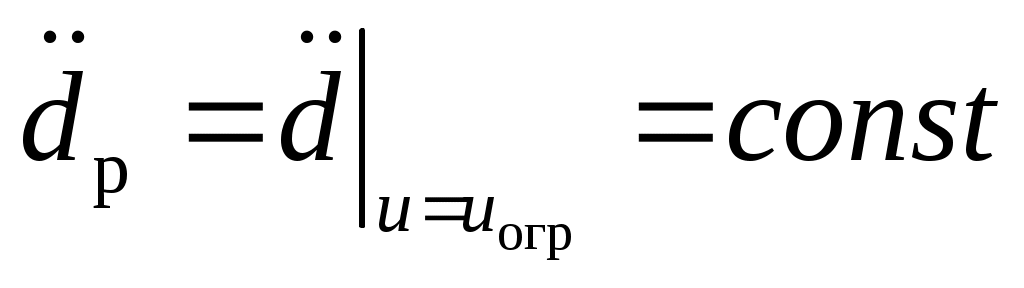 . (2.13) . (2.13)
Приравнивая уравнения (2.11) и (2.12), и решая их относительно дальности d, получим зависимость для определения расстояния до поверхности ограничения 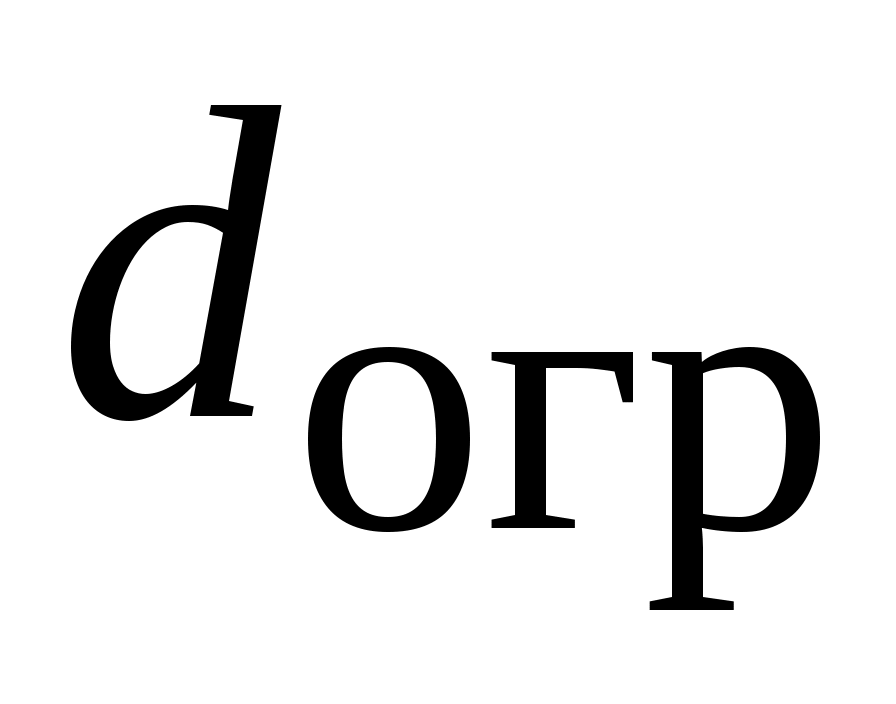 , при достижении которого необходимо включать управление (2.6). Проделав соответствующие преобразования, имеем , при достижении которого необходимо включать управление (2.6). Проделав соответствующие преобразования, имеем
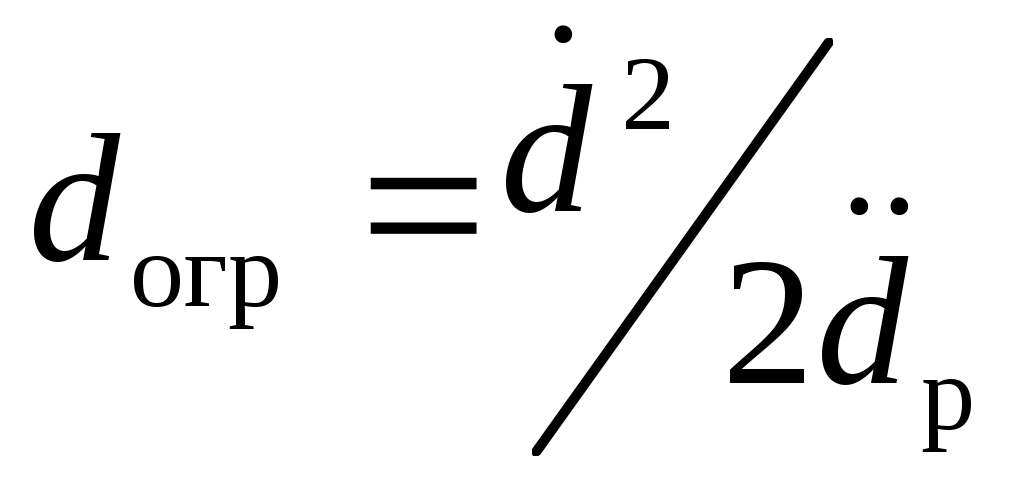 . (2.14) . (2.14)
В (2.14) 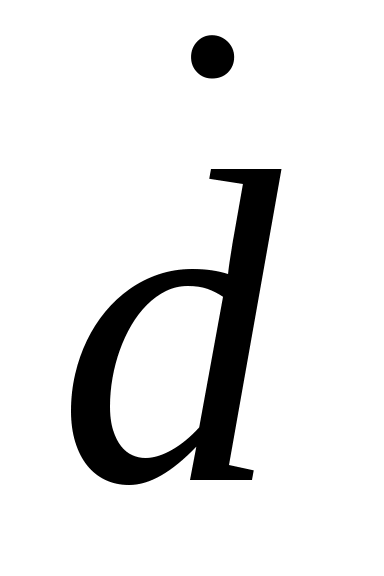 и и 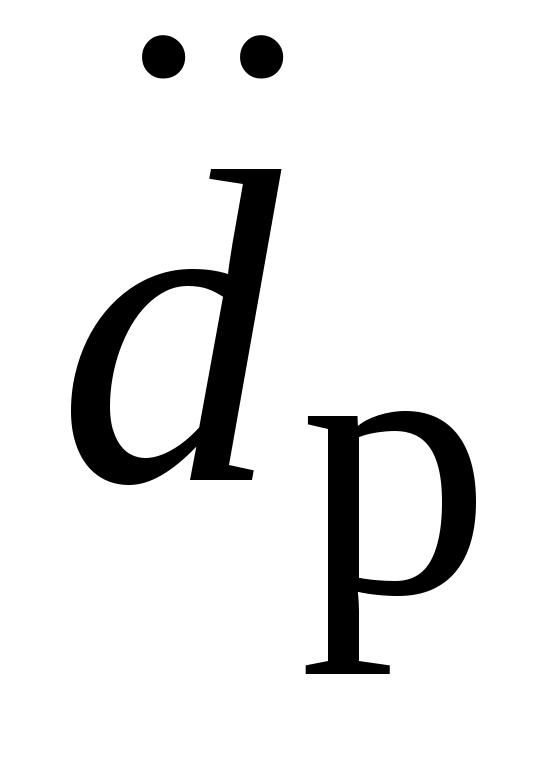 определяются путем формального нахождения первой и второй производной (с учетом (2.6)) от зависимости (2.5) по t как по параметру. Проделав данную процедуру, имеем определяются путем формального нахождения первой и второй производной (с учетом (2.6)) от зависимости (2.5) по t как по параметру. Проделав данную процедуру, имеем
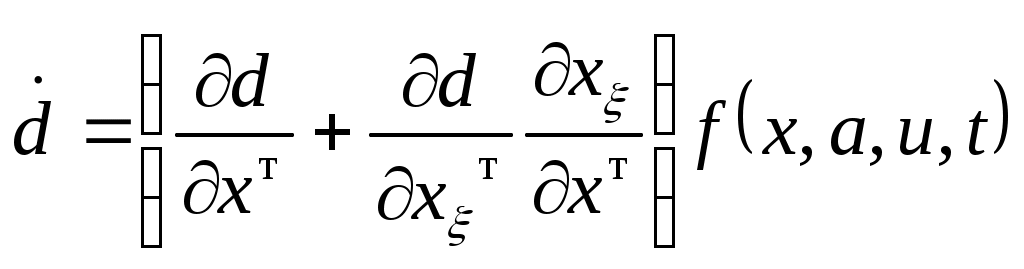 (2.15) (2.15)
и в линейной постановке
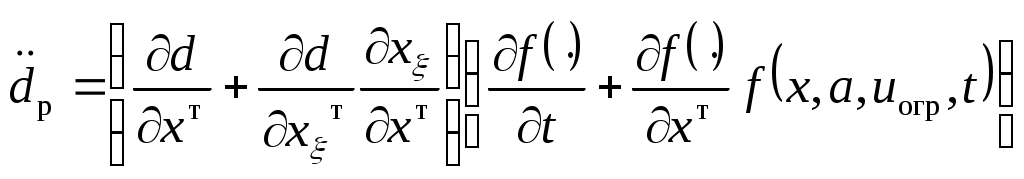 (2.16) (2.16)
(слагаемое 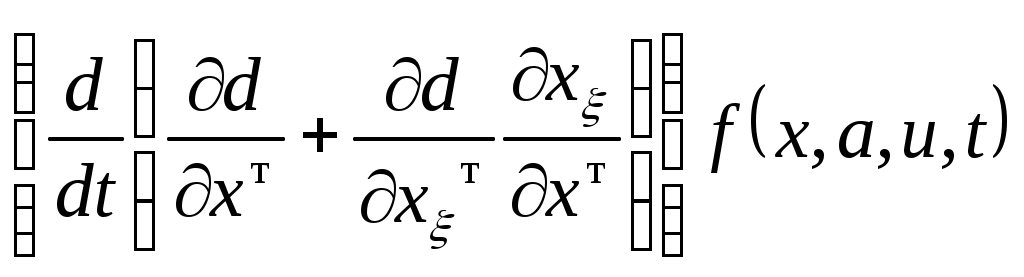 для упрощения дальнейших выкладок в (2.16) не учитывается). для упрощения дальнейших выкладок в (2.16) не учитывается).
Основной проблемой вычисления значений 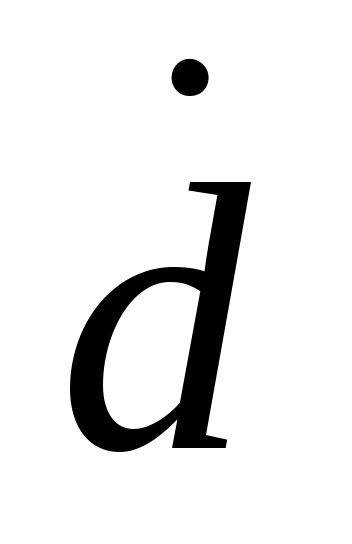 и и 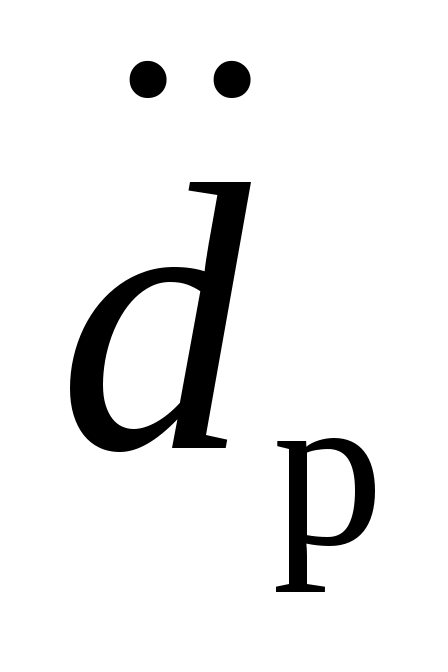 по (2.15), (2.16) является получение аналитической зависимости для частных производных по (2.15), (2.16) является получение аналитической зависимости для частных производных 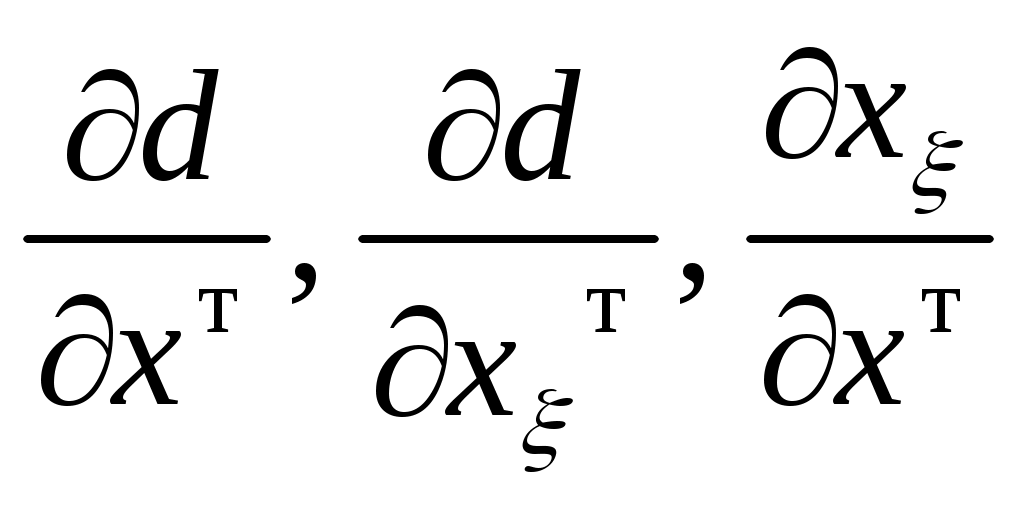 , физический смысл которых иллюстрируется на рис.2.3 (на рисунке приращение расстояния , физический смысл которых иллюстрируется на рис.2.3 (на рисунке приращение расстояния 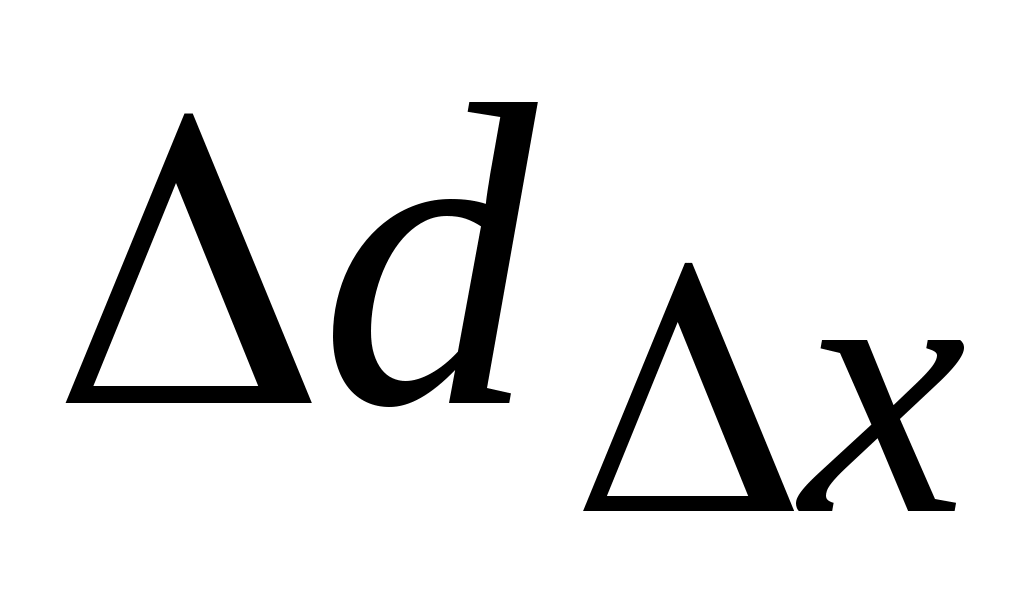 вызвано перемещением точки М(x) на величину вызвано перемещением точки М(x) на величину 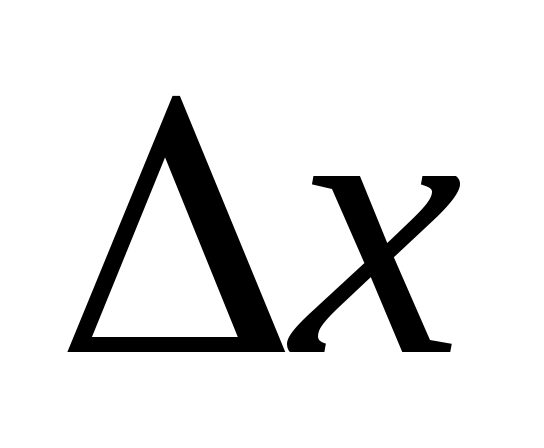 , а приращение , а приращение 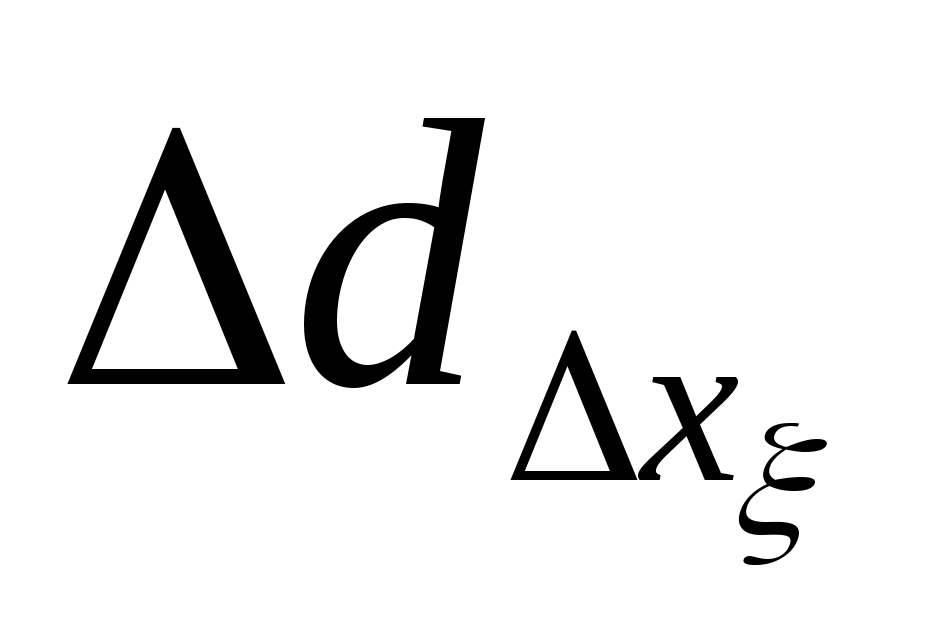 - смещением по поверхности - смещением по поверхности 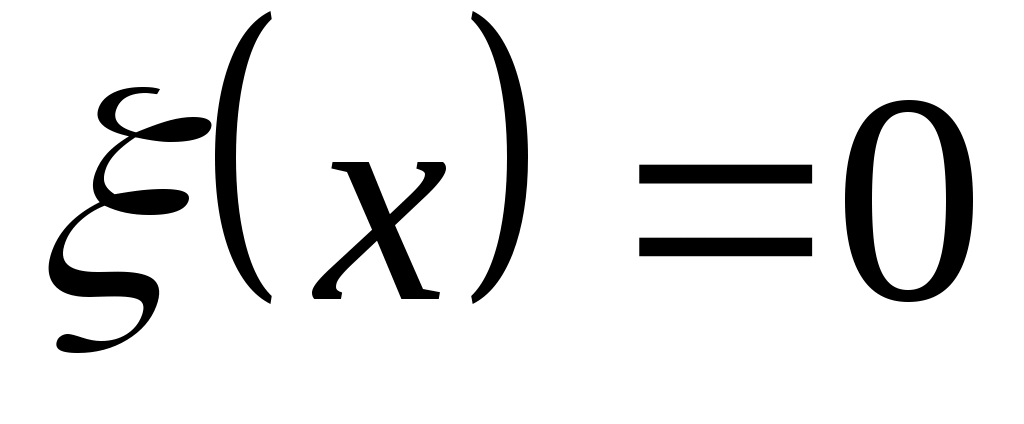 точки М(x) на величину точки М(x) на величину 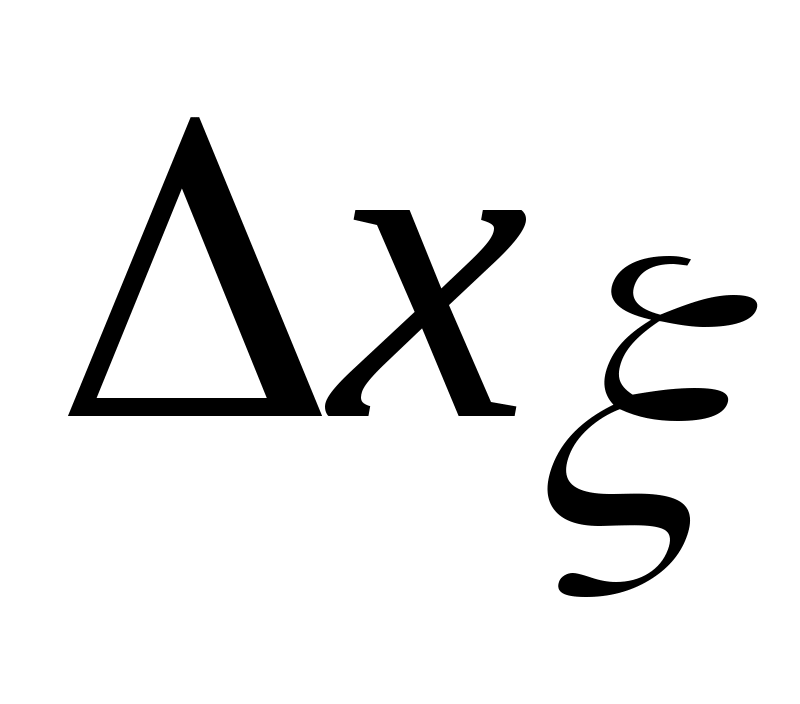 ). Эта проблема заключается в том, что в процедуре их вычисления присутствует, постоянно осуществляемая, операция минимизации функции (2.4). Если же динамическая система перемещается в пространстве ). Эта проблема заключается в том, что в процедуре их вычисления присутствует, постоянно осуществляемая, операция минимизации функции (2.4). Если же динамическая система перемещается в пространстве 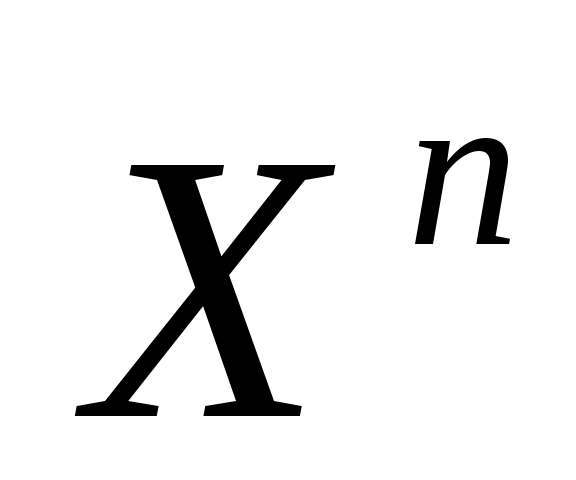 строго по нормали к поверхности ограничения строго по нормали к поверхности ограничения 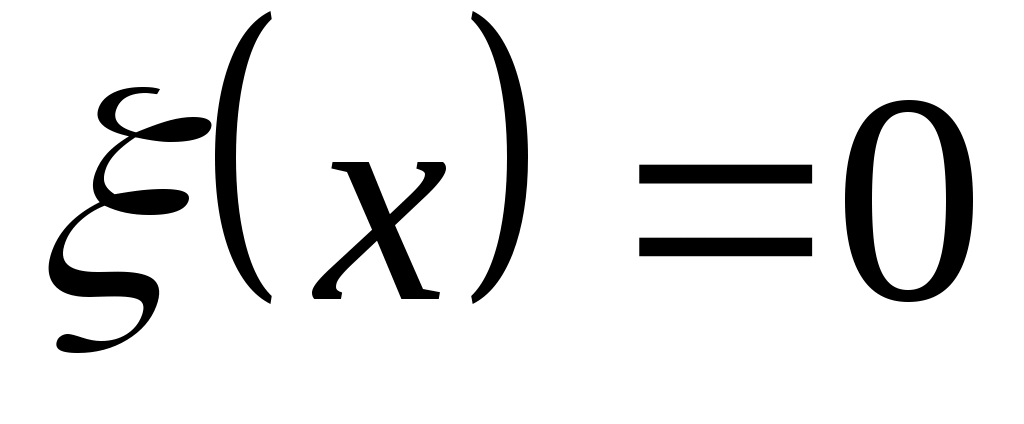 , то , то 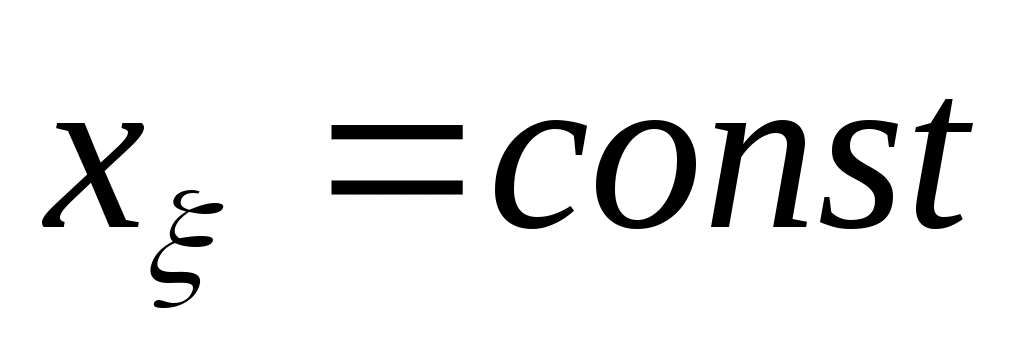 и первый сомножитель в (2.15) и (2.16) равен и первый сомножитель в (2.15) и (2.16) равен
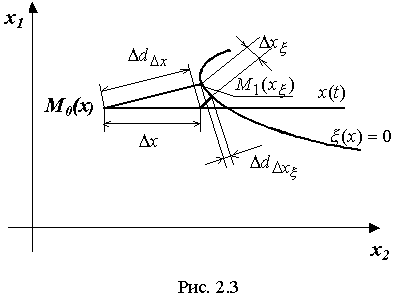 Рис.2.3 Рис.2.3
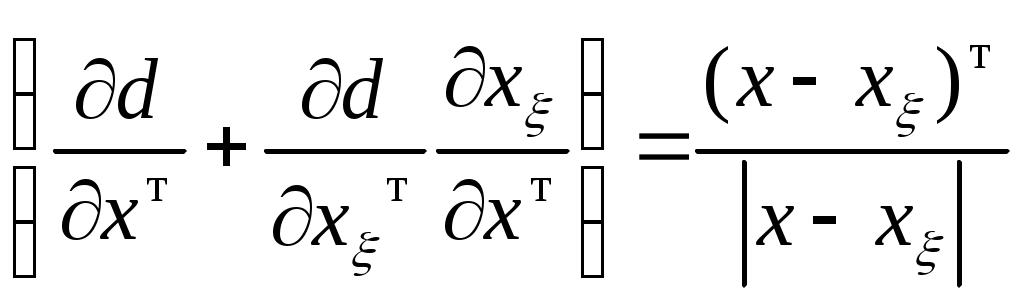 . .
Путь разрешения указанной проблемы будет представлен в последующих параграфах.
Анализ выражения (2.14) и его компонент (2.15), (2.16) показывает следующее.
Во-первых, при определении участка 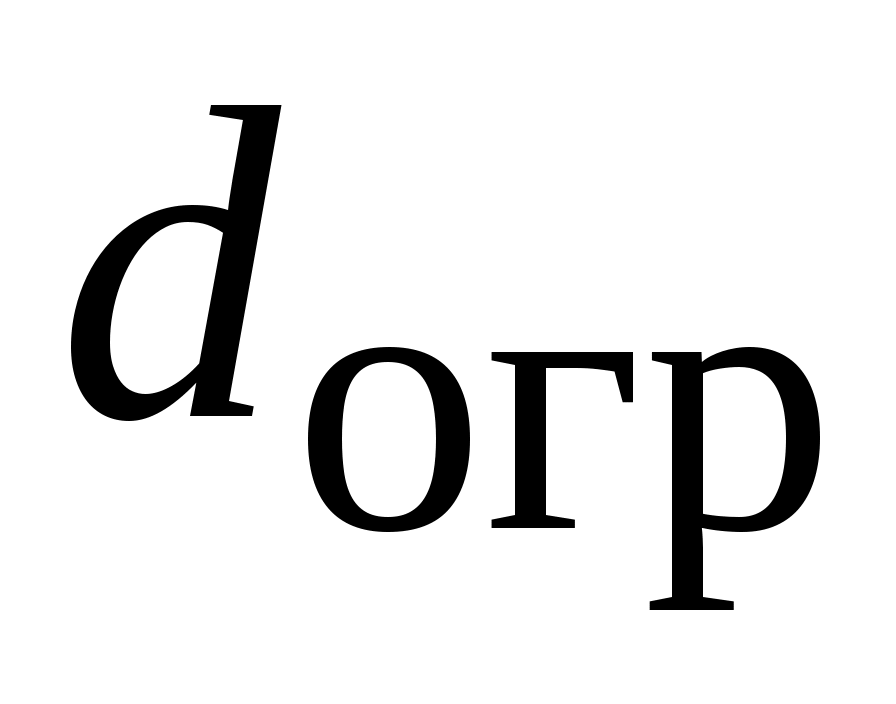 учитываются: учитываются:
собственные свойства ДС - 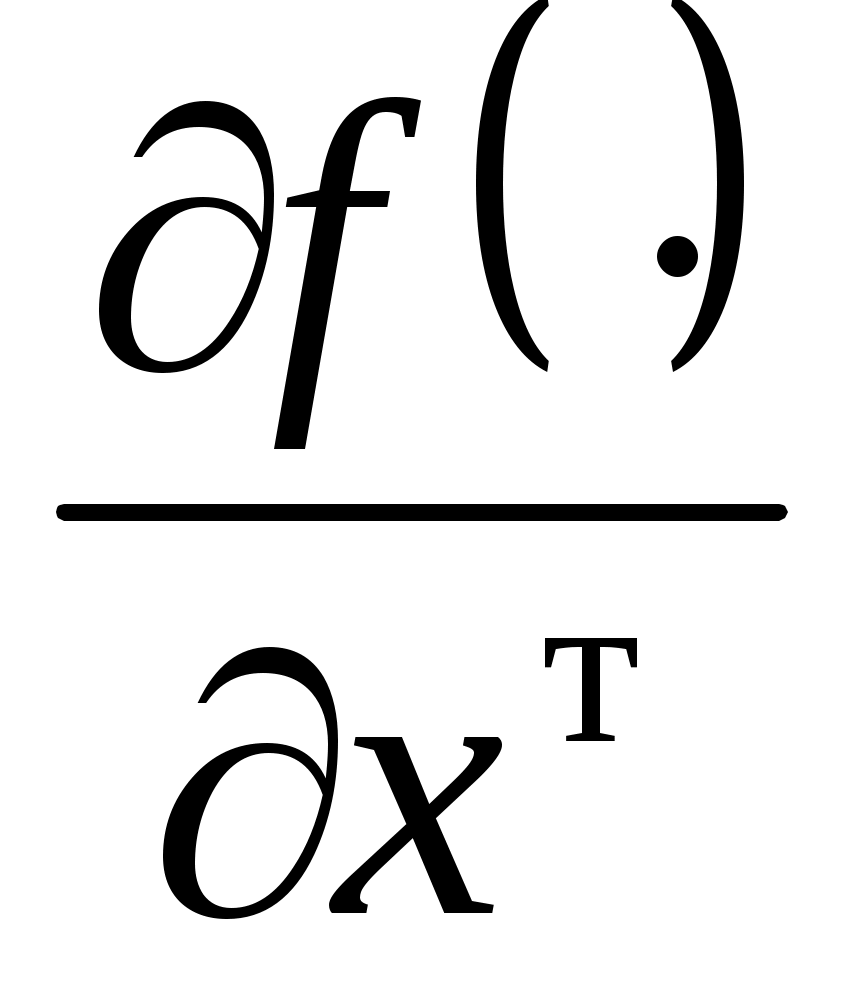 , ,
ее нестационарность - 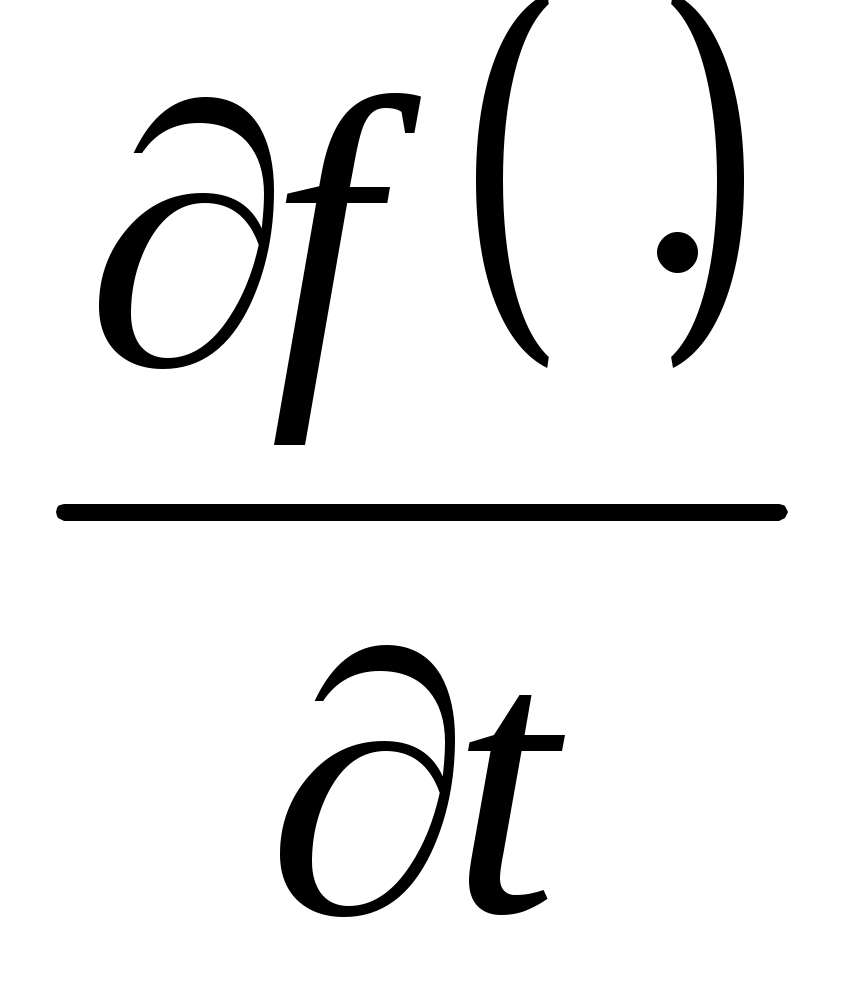 , ,
составляющая изменения расстояния до поверхности ограничения с учетом кривизны последней, в случае перемещения ДС по произвольной пространственной линии, не совпадающей с нормалью - 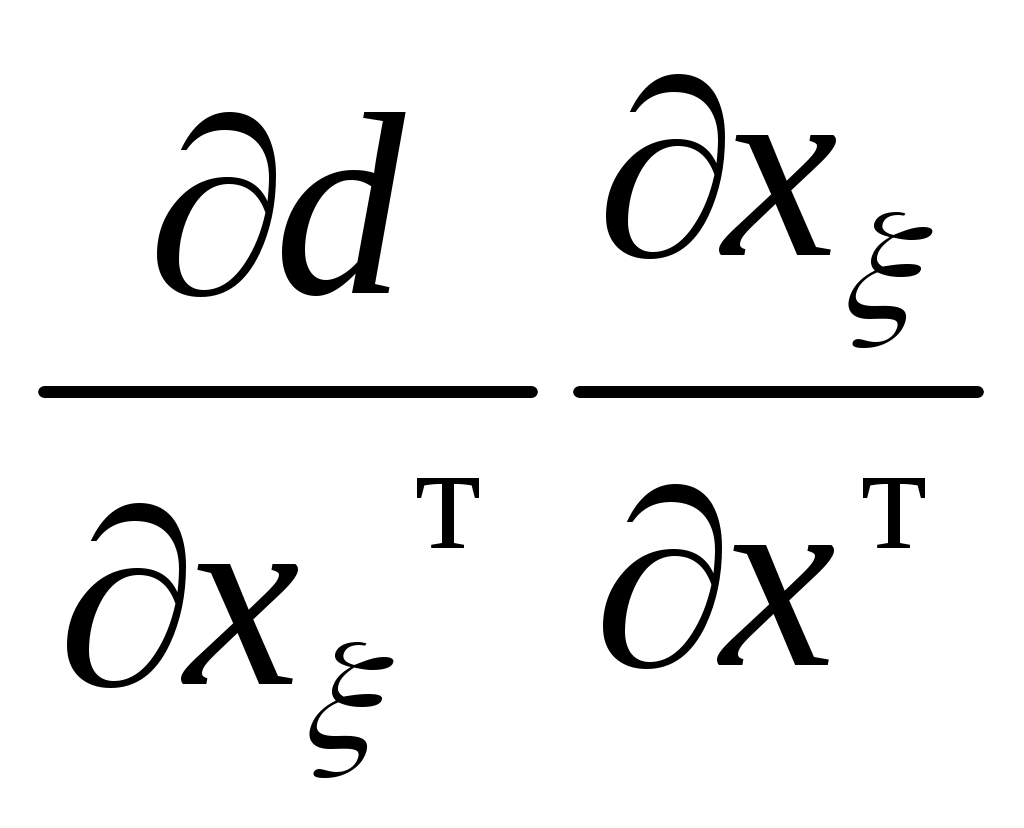 , ,
доверенное управление ограничения - 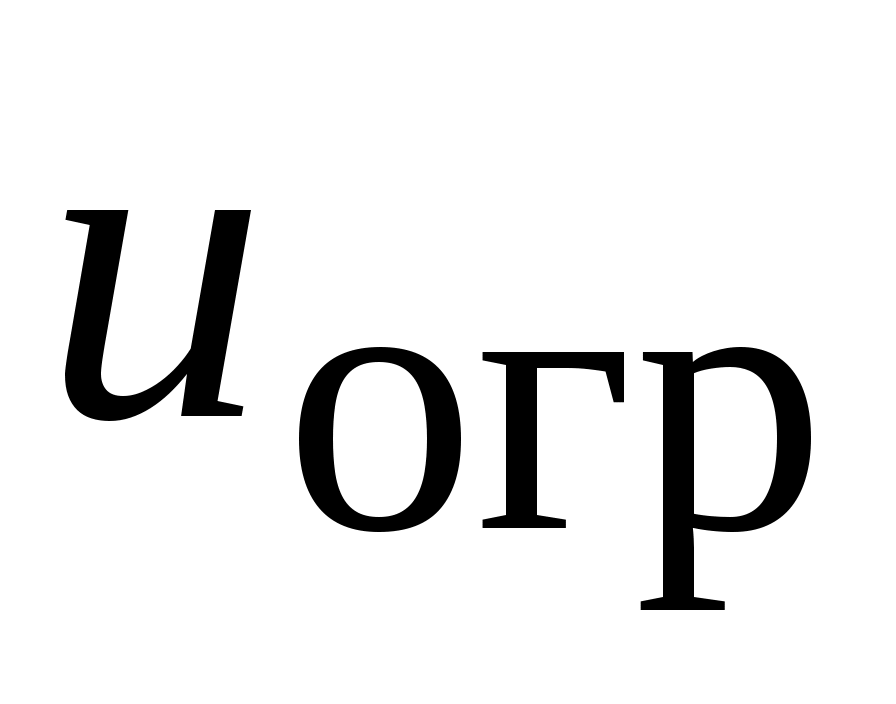 . .
Все это позволяет сделать вывод о наличии адаптационных свойств алгоритма выдерживания ограничений к конфигурации поверхности ограничения, свойствам среды и самой ДС.
Во-вторых: из (2.16) можно предположить, что под действием управления ограничения (2.6) произойдет изменение 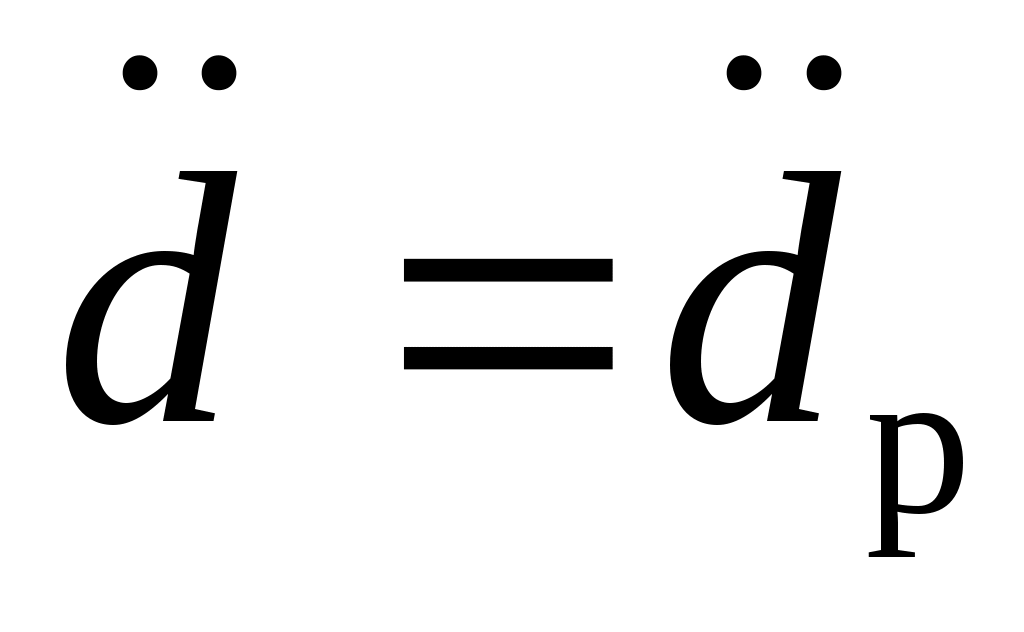 на участке ограничения, что противоречит основополагающему условию (2.13). Для его безусловного выполнения необходимо путем ведения компенсационного управления на участке ограничения, что противоречит основополагающему условию (2.13). Для его безусловного выполнения необходимо путем ведения компенсационного управления 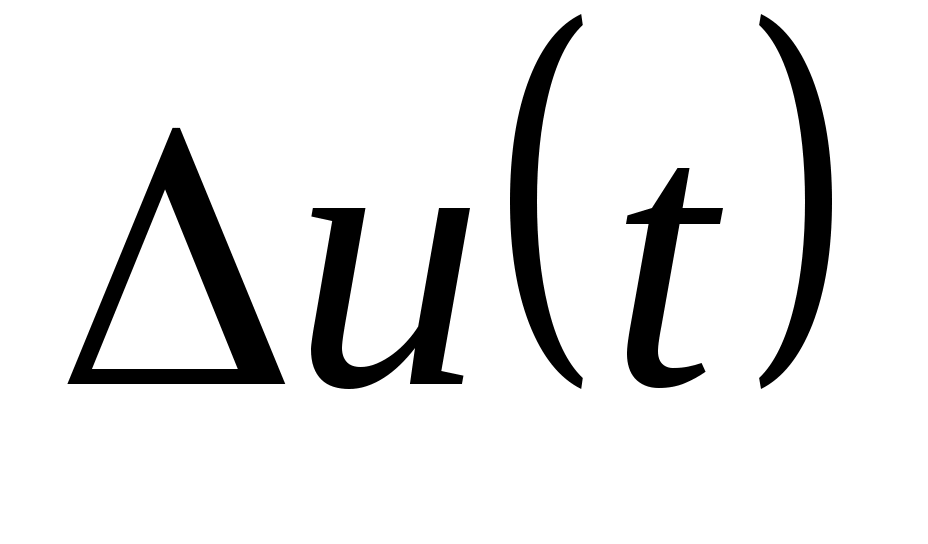 в (2.6), то есть, положив в (2.6), то есть, положив
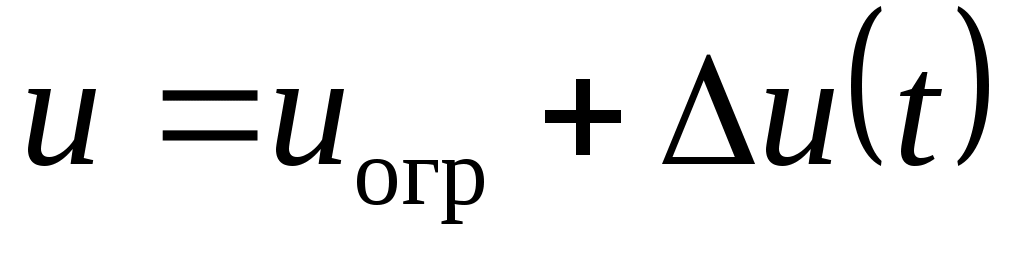 , ,
обеспечить
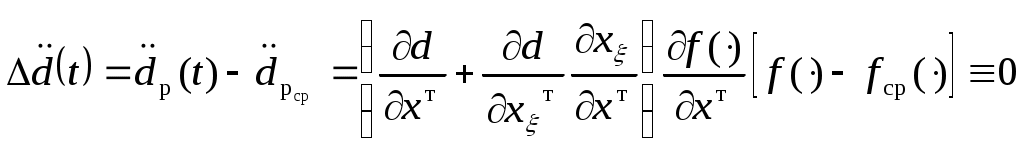 , (2.17) , (2.17)
где 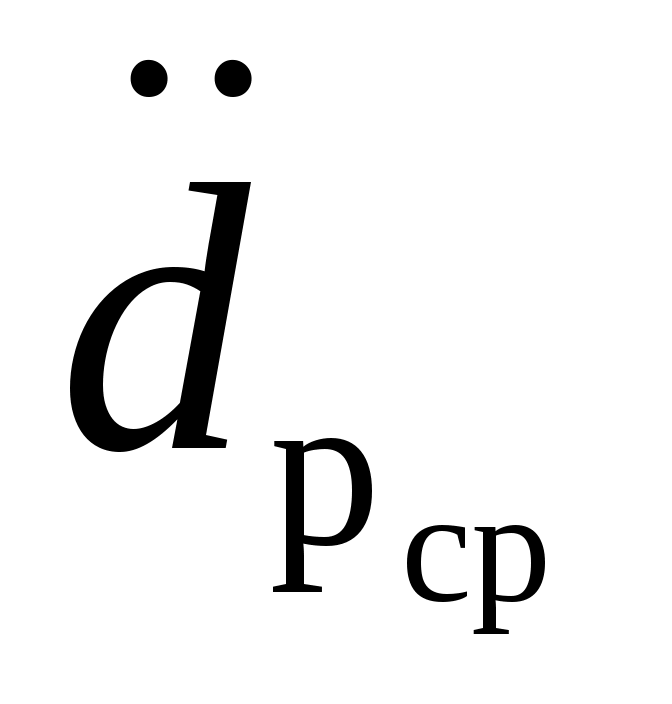 , , 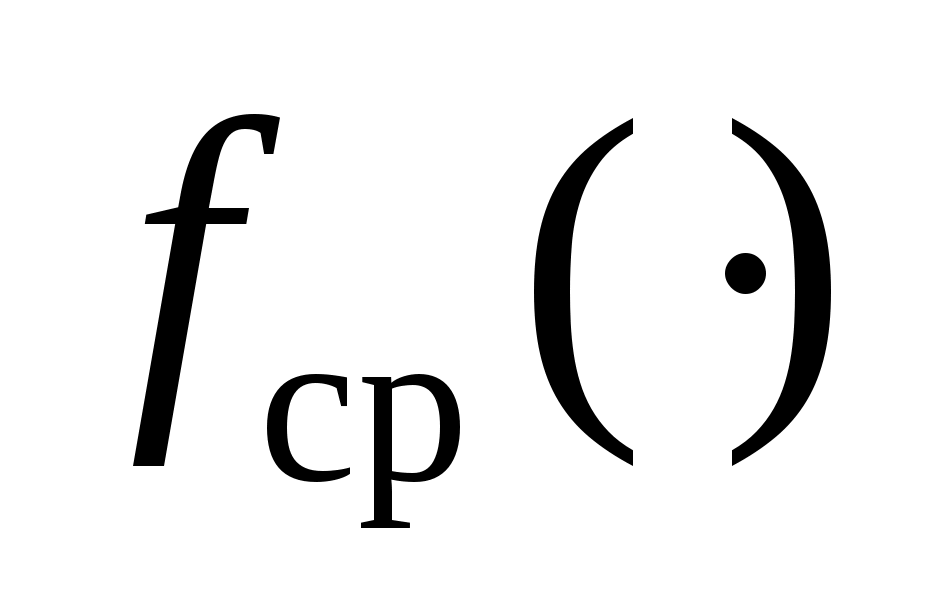 - располагаемое ускорение торможения и векторная функция - располагаемое ускорение торможения и векторная функция 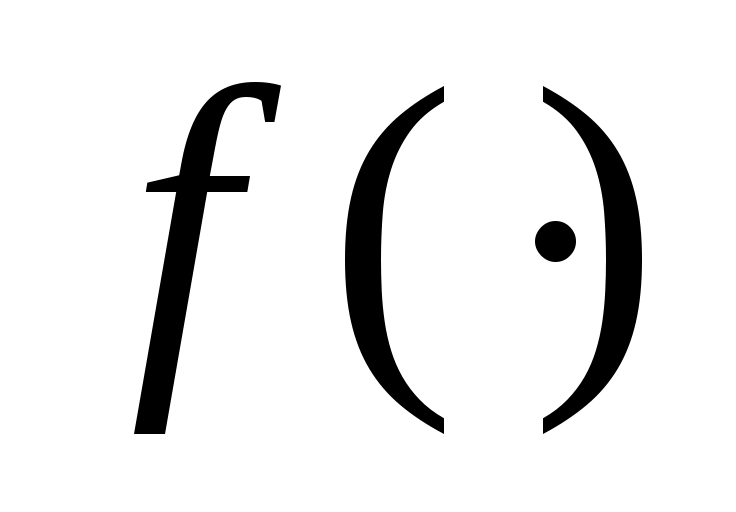 в момент срабатывания системы ограничения, соответственно. в момент срабатывания системы ограничения, соответственно.
В этом случае (2.16) можно переписать в виде
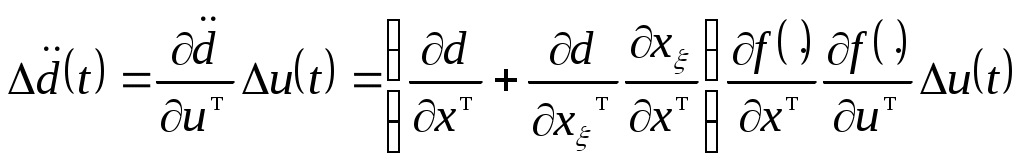 , (2.18) , (2.18)
откуда выразив 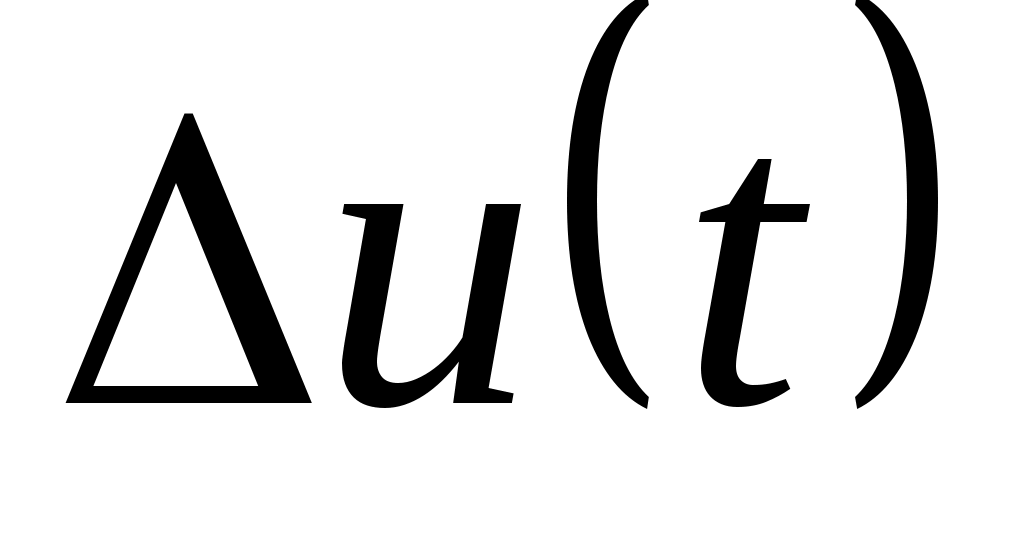
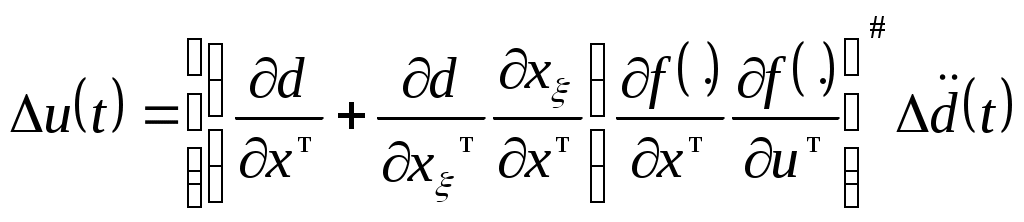 , ,
с учетом (2.17) получим выражение для компенсационного управления
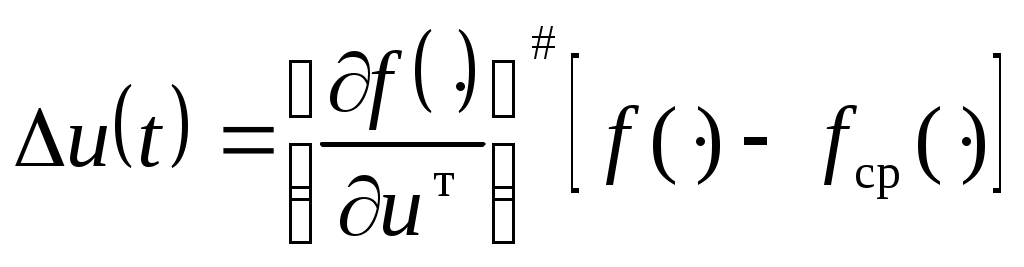 . (2.19) . (2.19)
Здесь и далее знак соответствует операции псевдообращения неквадратных и вырожденных матриц [25]. Необходимо отметить, что величина компенсационного управления 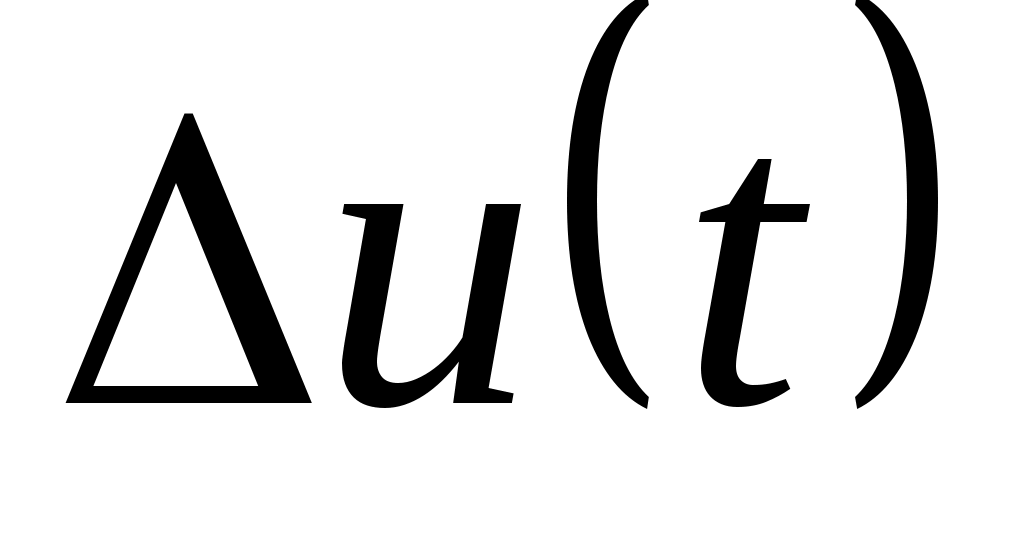 не зависит от параметров поверхности ограничения и расстояния до нее, а зависит только от свойств самой динамической системы. не зависит от параметров поверхности ограничения и расстояния до нее, а зависит только от свойств самой динамической системы.
В итоге для адаптивной системы выдерживания ограничения имеем следующий алгоритм ее срабатывания
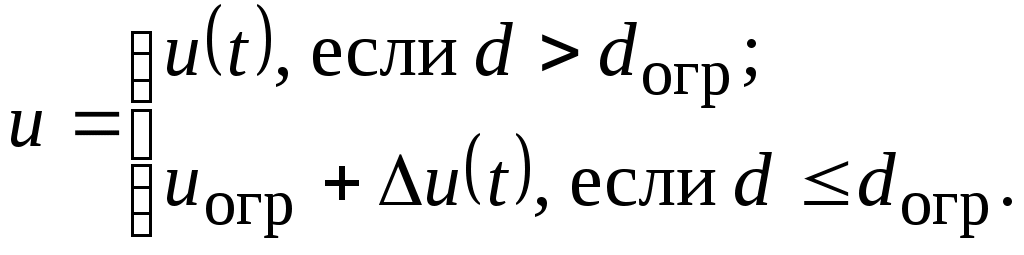 (2.20) (2.20)
В (2.20) 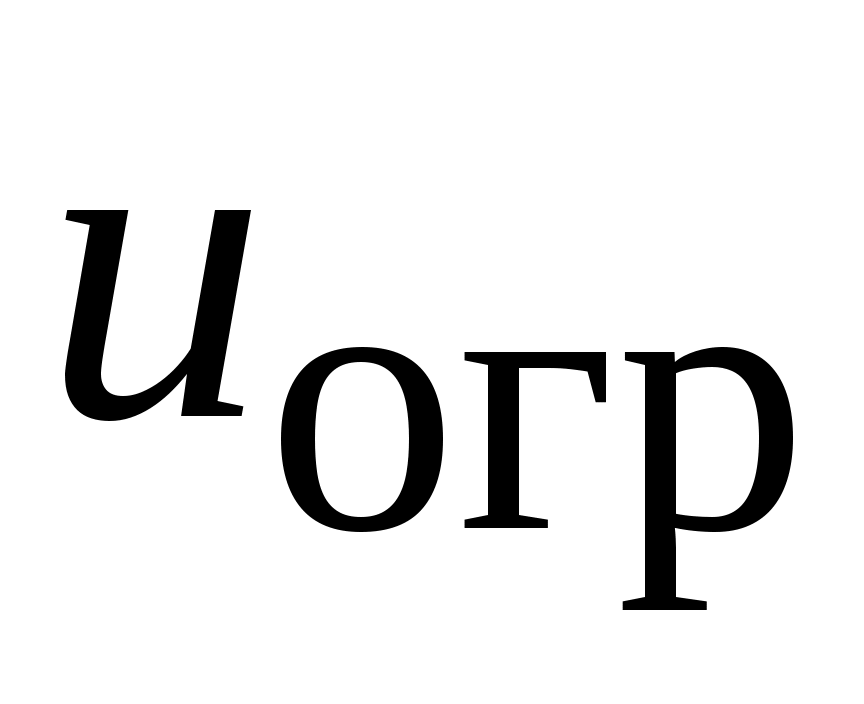 имеет смысл предварительно выбранного управляющего воздействия, доверенного системе выдерживания ограничений, а имеет смысл предварительно выбранного управляющего воздействия, доверенного системе выдерживания ограничений, а 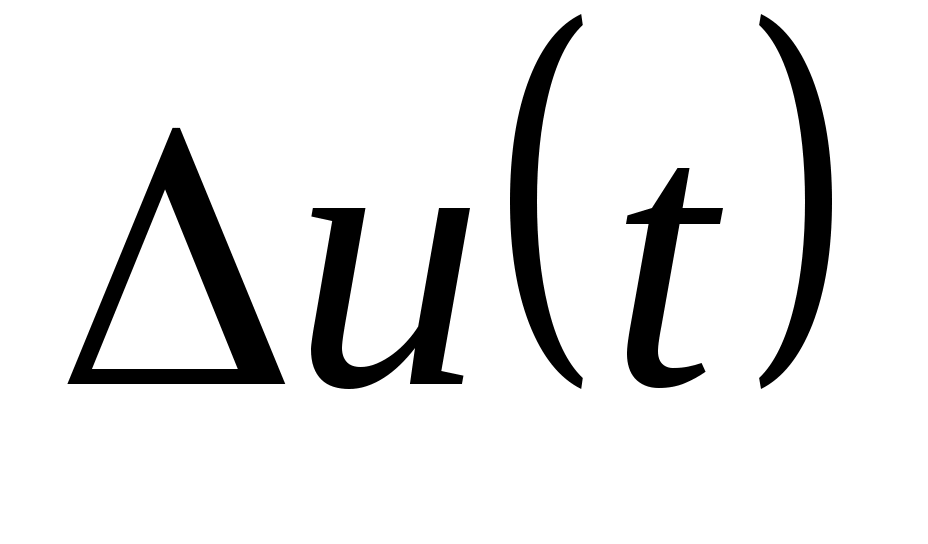 обеспечивает текущую подстройку алгоритма к нерасчетным условиям функционирования ДС. обеспечивает текущую подстройку алгоритма к нерасчетным условиям функционирования ДС.
|
|
|
 Скачать 4.57 Mb.
Скачать 4.57 Mb.

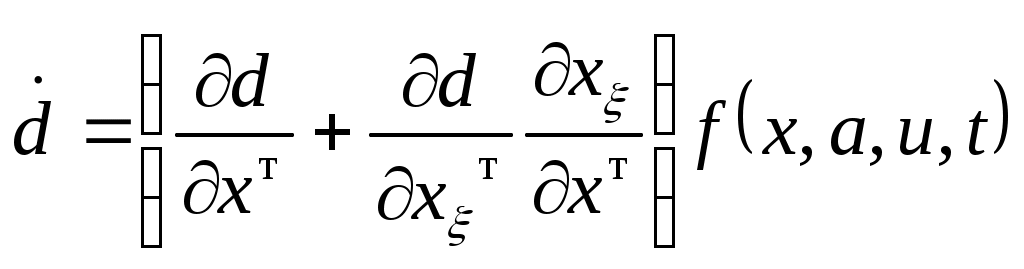 (2.15)
(2.15)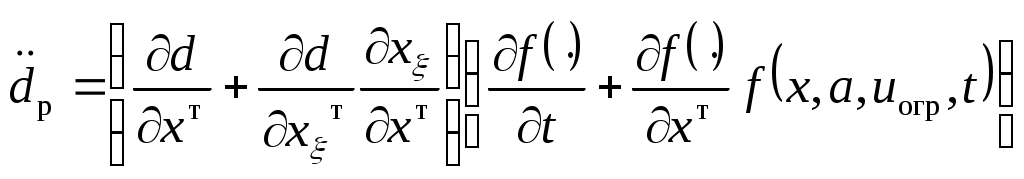 (2.16)
(2.16)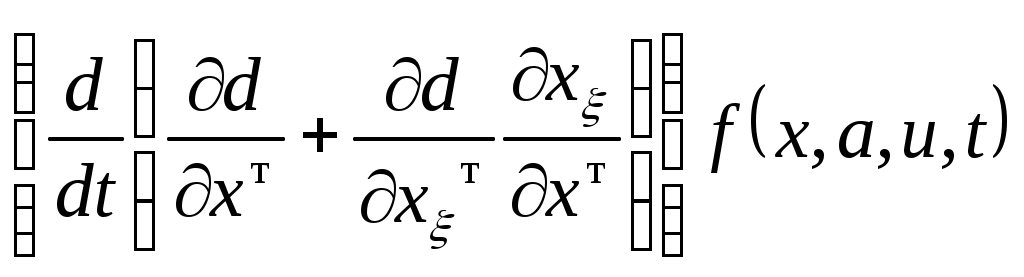 для упрощения дальнейших выкладок в (2.16) не учитывается).
для упрощения дальнейших выкладок в (2.16) не учитывается).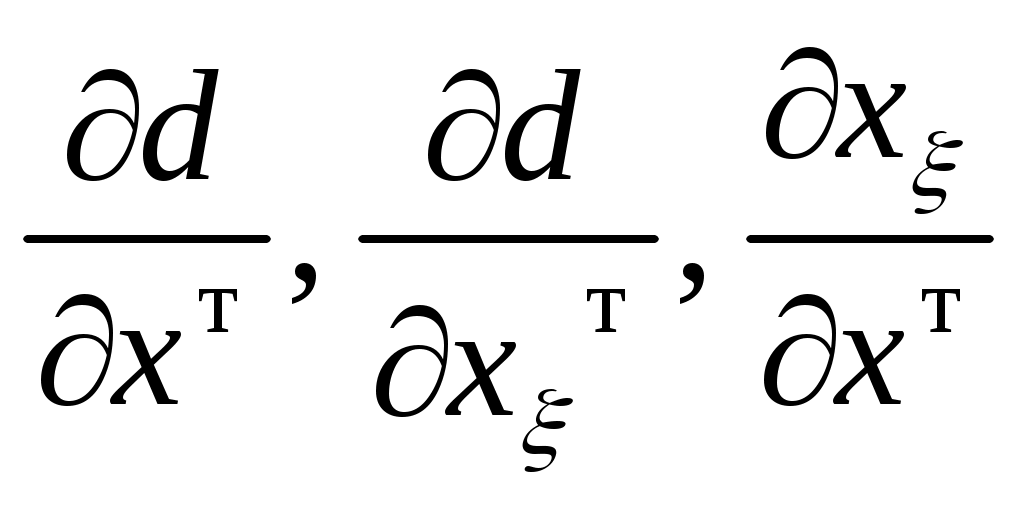 , физический смысл которых иллюстрируется на рис.2.3 (на рисунке приращение расстояния
, физический смысл которых иллюстрируется на рис.2.3 (на рисунке приращение расстояния  Рис.2.3
Рис.2.3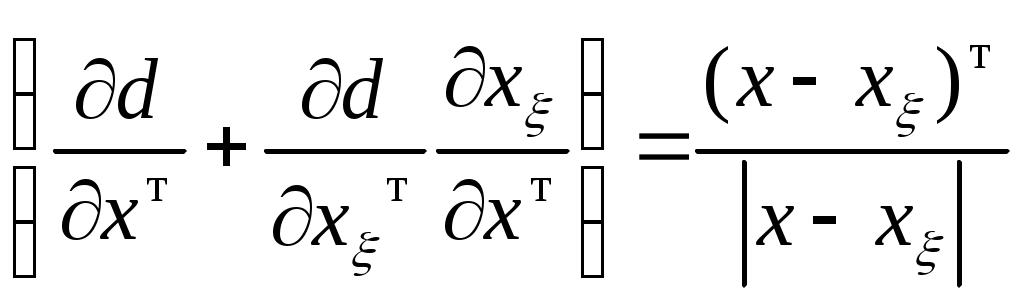 .
.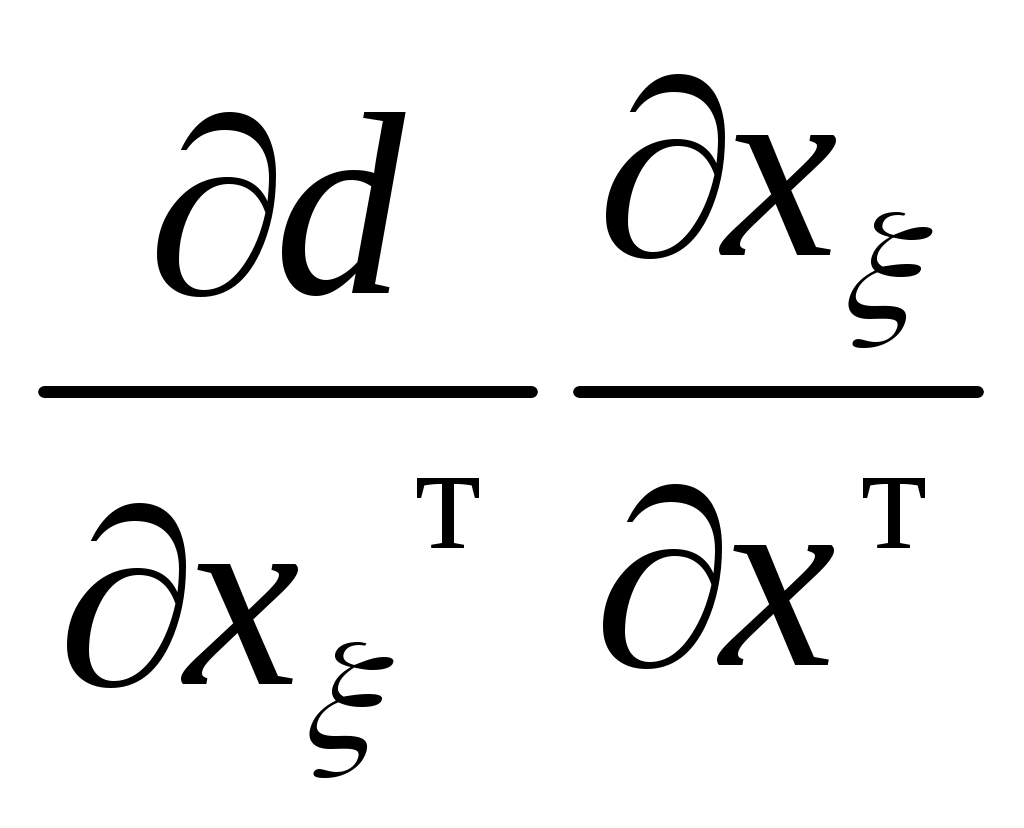 ,
,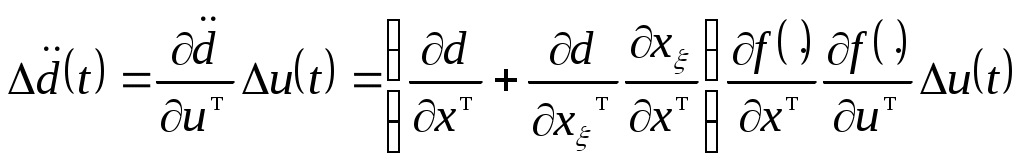 , (2.18)
, (2.18)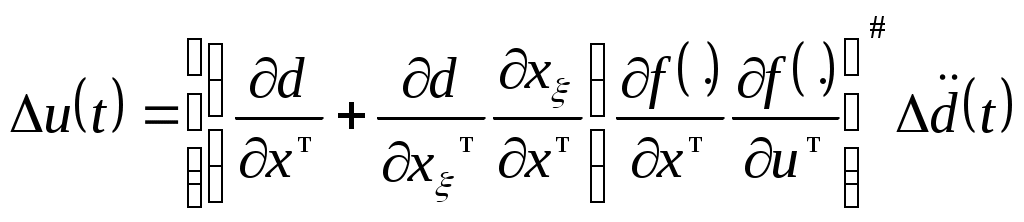 ,
,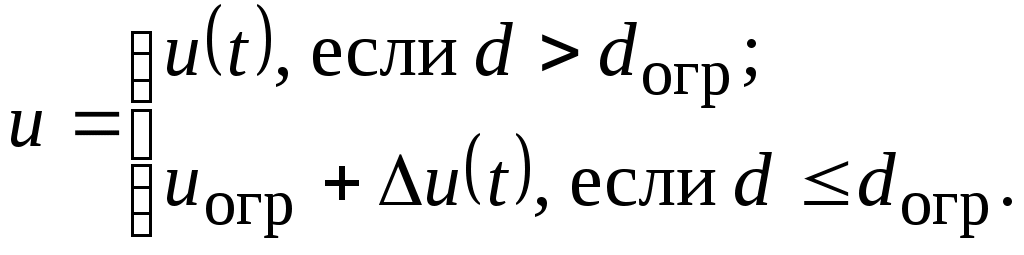 (2.20)
(2.20)