Системы ограничения. Текст монографии. Адаптивность к свойствам объекта, форме поверхности ограничения
 Скачать 4.57 Mb. Скачать 4.57 Mb.
|
3.3. Ограничение угла крена вертолетаСамо по себе накренение вертолета не таит опасности. Однако крен вертолета, из условий обеспечения безопасности полета на малых высотах, ограничивается величиной, пропорциональной текущей высоте. То есть, разрешенный крен в градусах соответствует количеству метров высоты. Вертолет как объект управления обладает рядом неблагоприятных характеристик устойчивости и управляемости, основными из которых являются малые демпфирующие моменты по угловым скоростям тангажу, крена и рыскания; статическая неустойчивость несущего винта по углу атаки; при наличии статической устойчивости по тангажу, крену и скорости полета, он не имеет динамической устойчивости по тангажу и скорости на всех режимах полета, а по крену – на режимах висения и полета с малыми скоростями; взаимосвязь движений по крену и рысканию в поступательном полете, которая ведет при полете с малыми скоростями к колебательной неустойчивости бокового движения, а на больших скоростях – к слабозатухающим колебаниям. Таким образом, вертолет как объект управления представляет собой достаточно сложную динамическую систему. При этом управление его угловым положением только по тангажу, крену либо рысканию приводит к необходимости перемещения командных рычагов управления по всем перечисленным координатам одновременно. В связи с этим, для получения основных зависимостей алгоритма выдерживания предельного крена вертолета необходимо рассмотреть как минимум пятимерное пространство состояний Х, вектор состояния которого включает следующие параметры и вектор управлений δ, включающий где 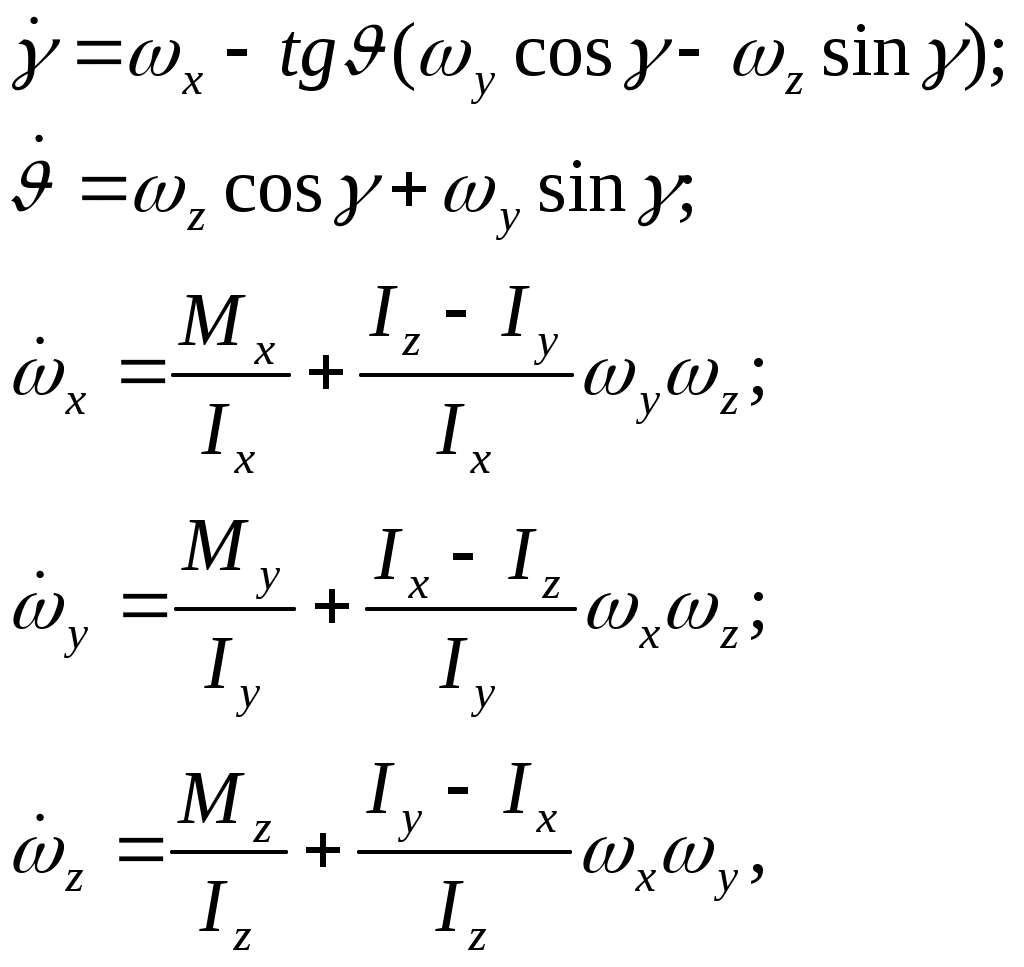 (3.31) (3.31)В 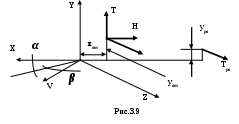 (3.31) моменты, действующие на вертолет определяются в соответствии со схемой сил, изображенной на рис.3.9. Таким образом где T, H, S – проекции результирующей силы несущего винта на связанные оси; Силы и моменты несущего винта задаются в виде Задавшись алгоритмом управления системы ограничения угла крена вертолета, применительно к отклонению автомата перекоса в канале крена, имеем 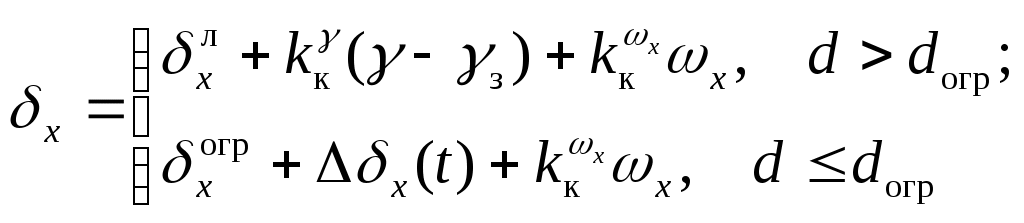 (3.33) (3.33)В канале тангажа отрабатывается закон САУ стабилизации углового положения. Воспользовавшись изложенным методом для общего случая ограничения, получим основные соотношения алгоритма. В итоге текущее расстояние до допустимого значения угла крена первая производная от расстояния d располагаемое ускорение торможения при наличии управления 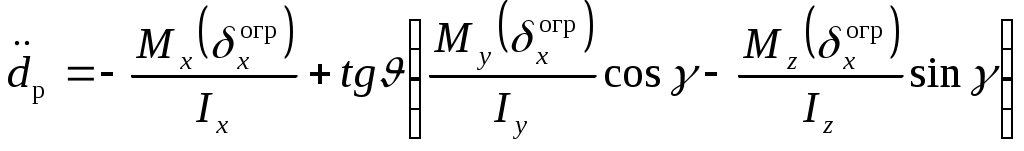 , ,(данное выражение получено с исключением из рассмотрения слагаемых второго порядка малости); коррекция управления на этапе ограничения 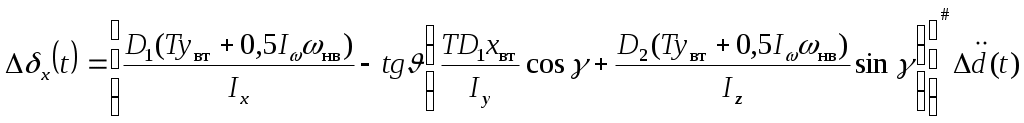 Р 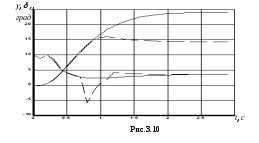 езультаты моделирования ограничения угла крена вертолета представлены на рис.3.10 – 3.11. Рис.3.10 иллюстрирует выход вертолета на угол крена 25° и его ограничение на уровне 15°. Небольшое перерегулирование, заметное на рисунке, объясняется учетом реальных свойств рулевого привода отклонения тарелки автомата перекоса при моделировании. Р  ис.3.11 характеризует адаптивные свойства алгоритма к изменению режима полета при аналогичной задаче ограничения. |
