Аздел
 Скачать 3.97 Mb. Скачать 3.97 Mb.
|
|
ТЕМА 1. Методы расчёта массы и параметров движения поездов. 1.1.1.0.1 На железнодорожном транспорте в тоннах измеряется следующая величина: а) масса состава; (+) б) удельное сопротивление движению; в) полное сопротивление движению. 1.1.1.1 Выражение для определения массы состава выводится из основного уравнения движения поезда для случая: а) равномерного движения; (+) б) ускоренного движения; в) замедленного движения. 1.1.1.2.1 Боксование колесных пар локомотива есть следствие: а) заклинивания колесных пар; б) нарушения основного закона локомотивной тяги; (+) в) неисправности тормозов; г) уменьшение сцепления в зоне колесо-рельс. (+) 1. 1.1.2.2 Зависимости параметров локомотива от скорости движения характеризуют: а) электротяговые характеристики; б) электромеханические характеристики; в) электродинамические характеристики; г) тяговые характеристики. (+) 1.1.1.2.3 С какой целью производится развеска локомотива: а) для удобства обслуживания оборудования; б) для увеличения сцепных свойств локомотива; (+) в) для соблюдения «классической» компоновки оборудования; г) для уменьшения воздействия на путь. 1.1.1.2.4 Какой из агрегатов Э.П.С. ограничивает высокую скорость движения: а) тяговые двигатели; б) тележки; в) тяговый трансформатор; г) выпрямители; д) пантограф. (+) 1.1.1.2.5 С какой целью производится развеска локомотива: а) для удобства обслуживания оборудования; б) для увеличения сцепных свойств локомотива; (+) в) для соблюдения «классической» компоновки оборудования; г) для уменьшения воздействия на путь. 1.1.1.2.6 Какой из агрегатов Э.П.С. ограничивает высокую скорость движения: а) тяговые двигатели; б) тележки; в) тяговый трансформатор; г) выпрямители; д) пантограф. (+) 1.1.1.2.7 Чем определяется величина коэффициента разгрузки колесной пары: а) положением шкворневого устройства; б) отношением моментов противоразгрузочных устройств; в) базой кузова и полной колесной базой; (+) г) шириной кузова. 1.1.1.2.8 Отношение максимальной силы тяги к сцепной массе локомотива определяется: а) коэффициентом сцепления; (+) б) коэффициентом трения; в) тормозным коэффициентом. 1.1.1.2.9 Отношение сцепной массы локомотива к его максимальной силе тяги определяется: а) коэффициентом сцепления; б) коэффициентом трения; в) тормозным коэффициентом; г) ничем не определяется. (+) 1.1.1.3.1 При движении поезда по прямому горизонтальному участку пути, на него действует: а) дополнительное сопротивление; б) основное сопротивление; (+) в) сопротивление при трогании с места. 1.1.1.3.2 При движении поезда по криволинейному горизонтальному участку пути, на него действует: а) дополнительное сопротивление; (+) б) основное сопротивление; (+) в) сопротивление при трогании с места. 1.1.1.3.3 При движении поезда по подъему, с которым совпадает кривая, на него действует: а) дополнительное сопротивление; (+) б) основное сопротивление; в) сопротивление при трогании с места. 1.1.1.3.4 Графическая зависимость в виде параболы, характеризует следующие зависимости: а) удельного сопротивления от скорости; (+) б) удельного сопротивления от нагрузки на ось; в) удельного сопротивления от массы состава. 1.1.1.3.5 Графическая зависимость в виде гиперболы, характеризует следующие зависимости: а) удельного сопротивления от скорости; б) удельного сопротивления от нагрузки на ось; (+) в) удельного сопротивления от массы состава. 1.1.1.3.6 Диаграмма удельных ускоряющих усилий соответствует режиму: а) тяги; (+) б) холостого хода; в) торможения. 1.1.1.4.1 На железнодорожном транспорте масса состава измеряется в: а) т;(+) б) кг; в) Н. 1.1.1.4.2 Расставьте знаки между величинами: масса локомотива, масса состава, масса поезда: а) >;>; б) <;<;(+) в) <;=. 1.1.1.4.3 Из основного уравнения движения поезда для случая равномерного движения выводится формула для определения: а) пройденного пути; б) времени движения; в) массы состава. (+) 1.1.1.4.4 Для расчетных параметров локомотива - Fкр и Vр определяется: а) масса локомотива; б) масса состава; (+) в) масса поезда. 1.1.1.5.1 Масса состава рассчитывается на: а) максимальном подъеме; б) максимальном спуске; в) расчетном подъеме. (+) 1.1.1.5.2 Расставьте знаки между величинами: масса поезда, масса состава, масса локомотива: а) >;>;(+) б) <;<; в) <;=. 1.1.1.5.3 Масса состава грузового поезда определяется: а) на самом трудном элементе профиля пути; (+) б) на самом легком элементе профиля пути; в) на станционном элементе. 1.1.1.5.4 Определите вес поезда по затяжному подъему, если известно: Fкр= 20000 кгс, 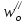 =1,8 кгс/т, =1,8 кгс/т, 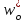 =2,1 кгс/т, iр=10,2о/оо; P=108 т. (Ответ введите в тоннах с точностью до 1 тонны.) =2,1 кгс/т, iр=10,2о/оо; P=108 т. (Ответ введите в тоннах с точностью до 1 тонны.)а)1400-1410 б)1520-1530 в) 1550-1560(+) 1.1.1.5.5 Определите вес поезда по затяжному подъему, если известно: Fкр=20000 кгс, 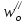 =1,8 кгс/т, =1,8 кгс/т, 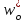 =2,1 кгс/т, Р=108 т, iр=6,2о/оо. (Ответ введите в тоннах с точностью до 1 тонны.) =2,1 кгс/т, Р=108 т, iр=6,2о/оо. (Ответ введите в тоннах с точностью до 1 тонны.)а) 2270-2300 б) 2380-2390(+) в)2300-2320 1.1.1.5.6 Определите вес поезда по затяжному подъему, если известно: Fкр =24200 кгс, 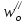 =1,5 кгс/т, =1,5 кгс/т, 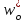 =2,1 кгс/т, Р=126 т, iр= 9,4о/оо. (Ответ введите в тоннах с точностью до 1 тонны.) =2,1 кгс/т, Р=126 т, iр= 9,4о/оо. (Ответ введите в тоннах с точностью до 1 тонны.)а)2070-2080 б)2060-2070 в) 2080-2090(+) 1.1.1.6.1 Масса состава рассчитывается при: а) расчетной скорости; (+) б) автоматической скорости; в) конструкционной скорости. 1.1.1.6.2 Определите вес поезда по затяжному подъему, если известно: Fкр =46200 кгс, 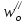 =1,7 кгс/т, =1,7 кгс/т, 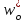 =2,1 кгс/т, Р=250 т, iр=12,4о/оо. (Ответ введите в тоннах с точностью до 1 тонны.) =2,1 кгс/т, Р=250 т, iр=12,4о/оо. (Ответ введите в тоннах с точностью до 1 тонны.)а) 3015-3025(+) б) 3010-3015 в)3025-3035 1.1.1.6.3 Определите вес поезда по затяжному подъему, если известно: Fкр =48200 кгс, 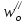 =1,5 кгс/т, =1,5 кгс/т, 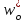 =2,1 кгс/т, Р=226 т, iр= 9,4 5о/оо. (Ответ введите в тоннах с точностью до 1 тонны.) =2,1 кгс/т, Р=226 т, iр= 9,4 5о/оо. (Ответ введите в тоннах с точностью до 1 тонны.)а)4170-4180 б) 4180-4190(+) в)4190-4200 1.1.2.1 Какая из перечисленных величин будет большей: а) масса локомотива; б) масса состава; в) масса поезда. (+) 1.1.2.3.1 Тонно-километровая диаграмма есть зависимость массы состава от следующих параметров: а) скорости движения; б) времени движения; в) профиля движения. (+) 1.1.2.3.2 На основании тонно-километровой диаграммы масса состава выбирается: а) наименьшей; б) наибольшей; в) средней. 1.1.2.4.1 Для определения унифицированной массы состава грузового поезда необходимо рассчитать и построить следующие зависимости: а) удельные равнодействующие усилия; б) тонно-километровую диаграмму; (+) в) тяговую характеристику локомотива. 1.1.2.4.2 На основании тонно-километровой диаграммы масса состава выбирается: а) наименьшей; б) наибольшей; в) средней. (+) 1.2.1.1.1 Механическая работа на преодоление кривой равна………. длины и радиуса кривой. а) произведению; б) частному; (+) в) сумме 1.2.1.1.2 Для определения работы, затрачиваемой на преодоление элемента профиля пути необходимо найти: а) произведение уклона на его длину; (+) б) частное длины и уклона элемента пути; в) сумму длины и уклона. 1.2.1.2.1 Результирующий спрямленный уклон равен…. спрямленного уклона и фиктивного подъема. а) сумме; (+) б) разности; в) произведению 1.2.1.2.2 Тангенс угла наклона элемента профиля пути равен: а) величине уклона элемента; (+) б) длине элемента; в) кривизне элемента. 1.2.1.2.3 На рисунке показано расположение поезда на подробном попикетном профиле: определите мгновенное значение уклона, действующее на поезд, если дано: вес состава 2100 т, длина состава 420 м, вес локомотива 256 т, длина локомотива 36 м. Примечание уклон указывать с точностью до 0,1 с учетом знака (подъем без знака, а спуск со знаком «-»).  а) 2,4 б) 4,4 в) 2,6(+) 1.2.1.2.4 На рисунке показано расположение поезда на подробном попикетном профиле: определите мгновенное значение уклона, действующее на поезд, если дано: вес состава 2500 т, длина состава 440 м, вес локомотива 256 т, длина локомотива 36 м. Примечание уклон указывать с точностью до 0,1 с учетом знака (подъем без знака, а спуск со знаком «-»).  а) 3,3 б) 3,4(+) в) 3,2 1.2.1.2.5 На рисунке показано расположение поезда на подробном попикетном профиле: определите мгновенное значение уклона, действующее на поезд, если дано: вес состава 3100 т, длина состава 450 м, вес локомотива 256 т, длина локомотива 36 м. Примечание уклон указывать с точностью до 0,1 с учетом знака (подъем без знака, а спуск со знаком «-»).  а) 1,1-1,2 б) 1,3-1,4(+) в) 1,5-1,6 1.2.1.2.6 На рисунке показано расположение поезда на подробном попикетном профиле: определите мгновенное значение уклона, действующее на поезд, если дано: вес состава 2100 т, длина состава 420 м, вес локомотива 256 т, длина локомотива 36 м. Примечание уклон указывать с точностью до 0,1 с учетом знака (подъем без знака, а спуск со знаком «-»).  а) 2,4(+) б) 0,6 в) 2,3 1.2.1.2.7 На рисунке показано расположение поезда на подробном попикетном профиле: определите мгновенное значение уклона, действующее на поезд, если дано: вес состава 4100 т, длина состава 430 м, вес локомотива 120 т, длина локомотива 18 м. Примечание уклон указывать с точностью до 0,1 с учетом знака (подъем без знака, а спуск со знаком «-»).  а) 0,6 б) 0,3(+) в) 0,2 1.2.1.3.1 Отношение длины кривой к радиусу кривой элемента профиля пути характеризует: а) дополнительное сопротивление движению от кривизны пути при Lп б) дополнительное сопротивление движению от кривизны пути при Lп>Lкр; в) дополнительное сопротивление движению от кривизны пути при Lп= Lкр; (+) 1.2.1.3.2 Отношение длины кривой к радиусу кривой элемента профиля пути, умноженному на отношение длины поезда к длине элемента, характеризует: а) дополнительное сопротивление движению от кривизны пути при Lп б) дополнительное сопротивление движению от кривизны пути при Lп>Lкр; (+) в) дополнительное сопротивление движению от кривизны пути при Lп= Lк 1.2.1.3.3 От чего не зависит безопасность движения локомотива в кривых участках пути: а) от скорости движения; б) от нагрузок от колесных пар на рельсы; в) от бокового давления колеса на рельс; г) от температуры окружающей среды. (+) 1.2.1.3.4 Фиктивным подъемом профиля пути заменяют: а) кривую; (+) б) приведенный уклон; в) спрямленный уклон. 1.2.1.3.5 Замените приведенный на рисунке участок пути, содержащий кривую прямым, путем приведения сопротивления от кривой к уклону в обоих направлениях. Ответ укажите с точностью до 0,1, сначала в направлении «туда», а потом «обратно», введя результат с учетом знака через «;». На рисунке Lкр – длина кривой (м); Rкр – радиус кривой (м). 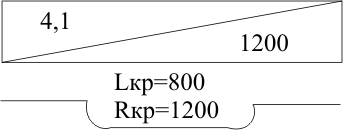 а) 4,7-5,7 б) 3,6-4,2 в) 4,5-3,7(+) 1.2.1.3.6 Замените приведенный на рисунке участок пути, содержащий кривую прямым, путем приведения сопротивления от кривой к уклону в обоих направлениях. Ответ укажите с точностью до 0,1, сначала в направлении «туда», а потом «обратно», введя результат с учетом знака через «;». На рисунке Lкр – длина кривой (м); Rкр – радиус кривой (м). 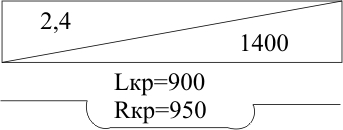 а) 1,5-2,5 б) 2,9-1,9(+) в)3,0-4,0 1.2.1.3.7 Замените приведенный на рисунке участок пути содержащий кривую прямым, путем приведения сопротивления от кривой к уклону в обоих направлениях. Ответ укажите с точностью до 0,1, сначала в направлении «туда», а потом «обратно», введя результат с учетом знака через «;». На рисунке Lкр – длина кривой (м); Rкр – радиус кривой (м). 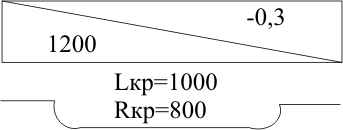 а) 0,4;1,0(+) б) 0,8; 1,2 в) 1,3; 1,4 1.2.1.3.8 Замените приведенный на рисунке участок пути содержащий кривую прямым, путем приведения сопротивления от кривой к уклону в обоих направлениях. Ответ укажите с точностью до 0,1, сначала в направлении «туда», а потом «обратно», введя результат с учетом знака через «;». На рисунке Lкр – длина кривой (м); Rкр – радиус кривой (м). 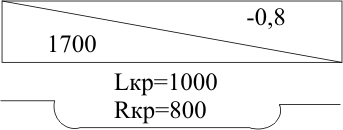 а) 0,5; 1,8 б) 0,7; 1,3 в) 0,3; 1,3(+) 1.2.1.3.9 Замените приведенный на рисунке участок пути содержащий кривую прямым, путем приведения сопротивления от кривой к уклону в обоих направлениях. Ответ укажите с точностью до 0,1, сначала в направлении «туда», а потом «обратно», введя результат с учетом знака через «;». На рисунке Lкр – длина кривой (м); Rкр – радиус кривой (м). 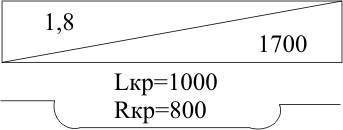 а) 2,0 – 1,5 б) 2,3 - 1,3(+) в) 2,2- 1,2 1.2.1.4.1 Какая величина численно равна величине уклона элемента: а) дополнительное сопротивление движению от уклона; (+) б) дополнительное сопротивление движению от кривизны пути; в) основное сопротивление движению. 1.2.1.4.2 Сумма спрямленного уклона и фиктивного подъема от кривой определяет: а) результирующий уклон; (+) б) суммарную длину; в) длину кривой. 1.2.1.5.1 Какая величина численно равна произведению длины элемента на его уклон: а) дополнительное сопротивление движению от уклона; б) дополнительное сопротивление движению от кривизны пути; в) основное сопротивление движению. г) механическая работа по преодолению уклона. (+) 1.2.1.5.2 Величина уклона профиля пути характеризует: а) сопротивление от кривой; б) сопротивление от уклона; (+) в) длину элемента. 1.2.1.5.3 Спрямите участок из представленных элементов, предварительно проверив возможность спрямления согласно «Правилам тяговых расчетов». Если спрямление возможно, в качестве ответа введите величину уклона спрямленного элемента с точностью до 0,1о/оо. Если спрямление проводить нельзя – введите цифру 100.  а) 2,4 б) 1,4(+) в)1,7 1.2.1.5.4 Спрямите участок из представленных элементов, предварительно проверив возможность спрямления согласно «Правилам тяговых расчетов». Если спрямление возможно, в качестве ответа введите величину уклона спрямленного элемента с точностью до 0,1о/оо. Если спрямление проводить нельзя – введите цифру 100.  а)1,7 б) 2,5(+) в)5,2 1.2.1.5.5 Спрямите участок из представленных элементов, предварительно проверив возможность спрямления согласно «Правилам тяговых расчетов». Если спрямление возможно, в качестве ответа введите величину уклона спрямленного элемента с точностью до 0,1о/оо. Если спрямление проводить нельзя – введите цифру 100.  а) 300 б) 400 в) 100(+) 1.2.1.5.6 Спрямите участок из представленных элементов, предварительно проверив возможность спрямления согласно «Правилам тяговых расчетов». Если спрямление возможно, в качестве ответа введите величину уклона спрямленного элемента с точностью до 0,1о/оо. Если спрямление проводить нельзя – введите цифру 100.  а) 10,4 б) 8,9 в) 9,5(+) 1.2.1.5.7 Спрямите участок из представленных элементов, предварительно проверив возможность спрямления согласно «Правилам тяговых расчетов». Если спрямление возможно, в качестве ответа введите величину уклона спрямленного элемента с точностью до 0,1о/оо. Если спрямление проводить нельзя – введите цифру 100.  а) 8,3 б) 8,5(+) в) 8,6 1.2.2.1 Дополнительное сопротивление движению подвижного состава от уклона численно равно: а) длине элемента; б) произведению длина на уклон; в) уклону элемента. (+) 1.2.2.2 Величина уклона может быть определена как: а) тангенс угла наклона; (+) б) синус угла наклона; в) косинус угла наклона. 1.2.2.3 Сопротивление движению от уклона равно: а) произведению уклона на его длину; б) частному длины и уклона элемента пути; в) самому уклону. (+) 1.2.3.1 Дополнительное сопротивление движению от кривизны пути равно: а) отношению радиуса кривой к длине кривой; б) отношению длины кривой к радиусу кривой; (+) в) произведению радиуса кривой на длину кривой. 1.3.1.1 При построении кривой скорости методом МПС полюс построения: а) находится по оси станции; б) находится по оси скорости; в) меняется в зависимости от уклона. (+) 1.3.1.2.1 В процессе движения поезда по перегону значения скорости изменяются в пределах: а) от расчетной до допустимой; (+) б) от нуля до конструкционной; в) от автоматической до допустимой. 1.3.1.2.2 При увеличении скорости движения локомотива, его мощность: а) остается неизменной; (+) б) уменьшается; в) увеличивается. 1.3.1.2.3 При уменьшении скорости движения локомотива, его мощность: а) уменьшается; б) остается неизменной; (+) в) увеличивается. 1.3.1.2.4 При увеличении скорости движения локомотива, его сила тяги, согласно тяговой характеристики: а) увеличивается; б) уменьшается; (+) в) остается неизменной. 1.3.1.2.5 При равномерном движении, скорость поезда стремится: а) увеличиваться; б) уменьшаться; в) оставаться неизменной. (+) 1.3.1.2.6 При ускоренном движении, скорость поезда стремится: а) увеличиваться; (+) б) уменьшаться; в) оставаться неизменной. 1.3.1.2.7 При замедленном движении, скорость поезда стремится: а) увеличиваться; б) уменьшаться; (+) в) оставаться неизменной. 1.3.1.2.8 При движении по затяжному подъему, равнодействующее усилие, действующее на поезд, будет: а) положительно; б) отрицательно; (+) в) равно нулю. 1.3.1.2.9 При движении по затяжному спуску, равнодействующее усилие, действующее на поезд, будет: а) положительно; (+) б) отрицательно; в) равно нулю. 1.3.1.2.10 При движении по затяжному горизонтальному участку, равнодействующее усилие, действующее на поезд, будет стремиться: а) увеличиваться; б) уменьшаться; в) к нулю. (+) 1.3.1.2.11 На рисунке показаны графики изменения скорости движения поезда при движении на затяжном расчетном подъеме. В каком из изображенных случаев подъем оказался коротким и вес поезда может быть увеличен за счет запаса кинетической энергии. Может оказаться, что во всех рассмотренных случаях подъем оказался затяжным, тогда введите цифру «0». Также может быть, что подъем оказался коротким в двух рассмотренных случаях, тогда введите цифры через точку с запятой: например 1;3. 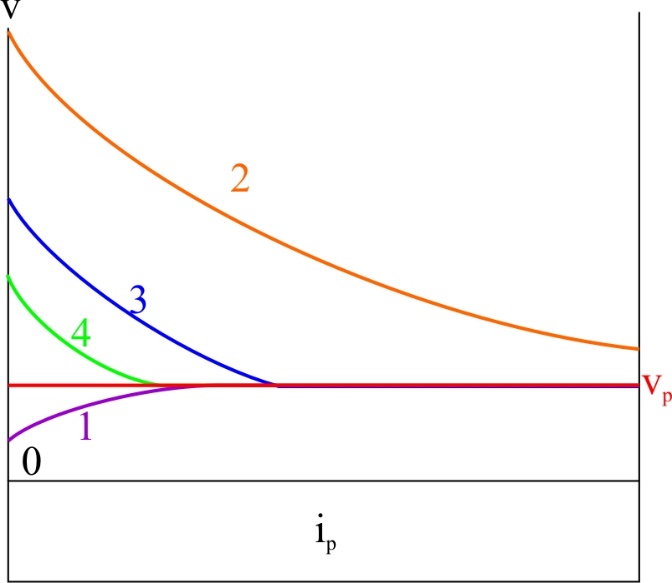 а) 2(+) б) 1 в) 4 1.3.1.2.12 На рисунке показаны графики изменения скорости движения поезда при движении на затяжном расчетном подъеме. В каком из изображенных случаев подъем оказался коротким и вес поезда может быть увеличен за счет запаса кинетической энергии. Может оказаться, что во всех рассмотренных случаях подъем оказался затяжным, тогда введите цифру «0». Также может быть, что подъем оказался коротким в двух рассмотренных случаях, тогда введите цифры через точку с запятой: например 1;3. 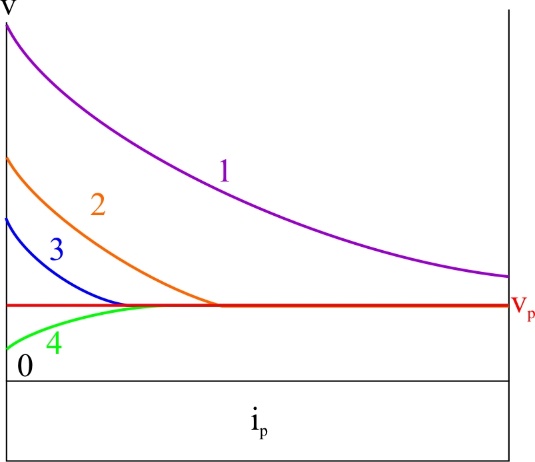 а) 0 б) 4 в) 1(+) 1.3.1.2.13 На рисунке показаны графики изменения скорости движения поезда при движении на затяжном расчетном подъеме. В каком из изображенных случаев подъем оказался коротким и вес поезда может быть увеличен за счет запаса кинетической энергии. Может оказаться, что во всех рассмотренных случаях подъем оказался затяжным, тогда введите цифру «0». Также может быть, что подъем оказался коротким в двух рассмотренных случаях, тогда введите цифры через точку с запятой: например 1;3. 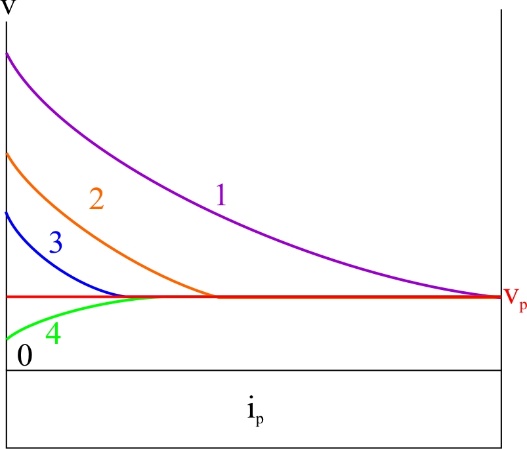 а) 0(+) б) 3 в) 4 1.3.1.2.14 На рисунке показаны графики изменения скорости движения поезда при движении на затяжном расчетном подъеме. В каком из изображенных случаев подъем оказался коротким и вес поезда может быть увеличен за счет запаса кинетической энергии. Может оказаться, что во всех рассмотренных случаях подъем оказался затяжным, тогда введите цифру «0». Также может быть, что подъем оказался коротким в двух рассмотренных случаях, тогда введите цифры через точку с запятой: например 1;3. 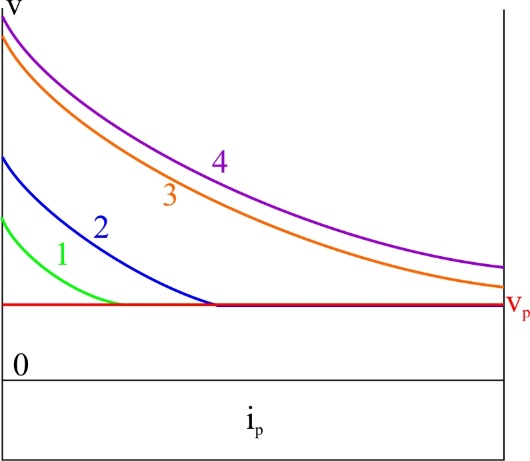 а) 2;1 б) 3;4(+) в) 2,4 1.3.1.2.15 На рисунке показаны графики изменения скорости движения поезда при движении на затяжном расчетном подъеме. В каком из изображенных случаев подъем оказался коротким и вес поезда может быть увеличен за счет запаса кинетической энергии. Может оказаться, что во всех рассмотренных случаях подъем оказался затяжным, тогда введите цифру «0». Также может быть, что подъем оказался коротким в двух рассмотренных случаях, тогда введите цифры через точку с запятой: например 1;3. 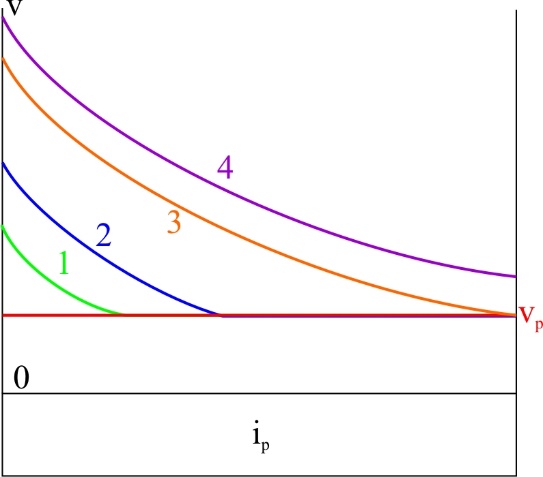 а) 4(+) б) 3 в) 1 1.3.1.2.16 Как следует рассматривать движение локомотива в кривых участках пути: а) как поступательное; б) как вращательное; в) как одновременно поступательное и вращательное; (+) г) как неустойчивое. 1.3.1.3.1 Кривая скорости – это графическая зависимость, которая: а) постоянно возрастает; б) постоянно убывает; в) то возрастает, то убывает. (+) 1.3.1.3.2 Разность окружной скорости и скорости поступательного движения поезда есть: а) скорость скольжения; (+) б) скорость качения; в) скорость виляния. 1.3.1.4 Масштабы для построения кривой скорости выводятся на основании действующих сил, согласно: а) основного закона локомотивной тяги; б) закона при торможении; в) уравнения движения поезда.(+) 1.3.1.5.1 Скорость скольжения колеса по рельсу равна ………… окружной скорости и скорости поступательного движения поезда. а) разности; (+) б) сумме; в) произведению. 1.3.1.5.2 Какая из ниже перечисленных скоростей определяется по формуле v= 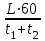 , где t1 и t2 время в чистом движении поезда по участку: , где t1 и t2 время в чистом движении поезда по участку:а) маршрутная скорость; б) участковая скорость; в) техническая скорость. (+) 1.3.1.6.1 Скорость движения локомотива увеличится, если диаметр колесной пары: а) уменьшить; б) увеличить; (+) в) оставить неизменным. 1.3.1.6.2 Скорость движения локомотива уменьшится, если диаметр колесной пары: а) уменьшить; (+) б) увеличить; в) оставить неизменным. 1.3.2.1.1 Существуют следующие методы определения времени движения поезда по железнодорожному участку: а) метод МПС; (+) б) метод РЖД; в) метод инженера Дегтярева.(+) 1.3.2.1.2 Существующие методы определения времени движения поезда по железнодорожному участку можно разделить на: а) аналитические; (+) б) вероятностные; в) графические(+) 1.3.2.2.1 При построении, каких кривых полюс построения меняется в зависимости от уклона: а) кривой скорости методом МПС; (+) б) кривой времени методом МПС; в) кривой времени методом инженера Дегтярева. 1.3.2.2.2 При построении, каких кривых полюс построения не зависит от уклона профиля пути: а) кривой скорости методом МПС; б) кривой времени методом МПС; (+) в) кривой времени методом инженера Дегтярева. (+) 1.3.2.2.3 При построении кривой времени методом МПС полюс построения: а) находится по оси станции; (+) б) находится по оси скорости; в) меняется в зависимости от уклона. 1.3.2.3.1 Кривая времени это графическая зависимость, которая: а) постоянно возрастает; (+) б) постоянно убывает; в) то возрастает, то убывает. 1.3.2.3.2 Постоянно возрастающими зависимостями являются следующие кривые: а) скорости; б) времени;(+) в) расхода энергоресурсов.(+) 1.3.2.4 Теоретическое обоснование определения времени методом МПС заключается в: а) дифференцировании уравнения движения поезда; б) интегрировании уравнения движения поезда;(+) в)масштабировании уравнения движения поезда. 1.3.2.5.1 Масштабы для построения кривой времени методом МПС выводятся на основании действующих сил, согласно: а) основного закона локомотивной тяги; б) закона при торможении; в) уравнения движения поезда.(+) 1.3.2.5.2 Масштабы для построения кривой времени методом инженера Дегтерева выводятся на основании действующих сил, согласно: а) уравнения движения поезда.(+) б) закона при торможении; в)основного закона локомотивной тяги; 1.3.2.6.1 Определение времени хода поезда методом инженера Дегтярева основывается на построении: а) равностороннего треугольника; б) равнобедренного треугольника; (+) в) прямоугольного треугольника. 1.3.2.6.2 В основе какого метода определение времени хода поезда основывается на построенииравнобедренных треугольников: а) метод МПС; б) метод инженера Дегтярева; (+) в) метод РЖД. 1.3.2.6.3 На рисунке приведены треугольники времени, определите те треугольники, которые не являются минутными. Необходимо указать все неминутные треугольники. Если таких треугольников несколько, то ответ вводится через «;». Если таких треугольников нет, введите 0. 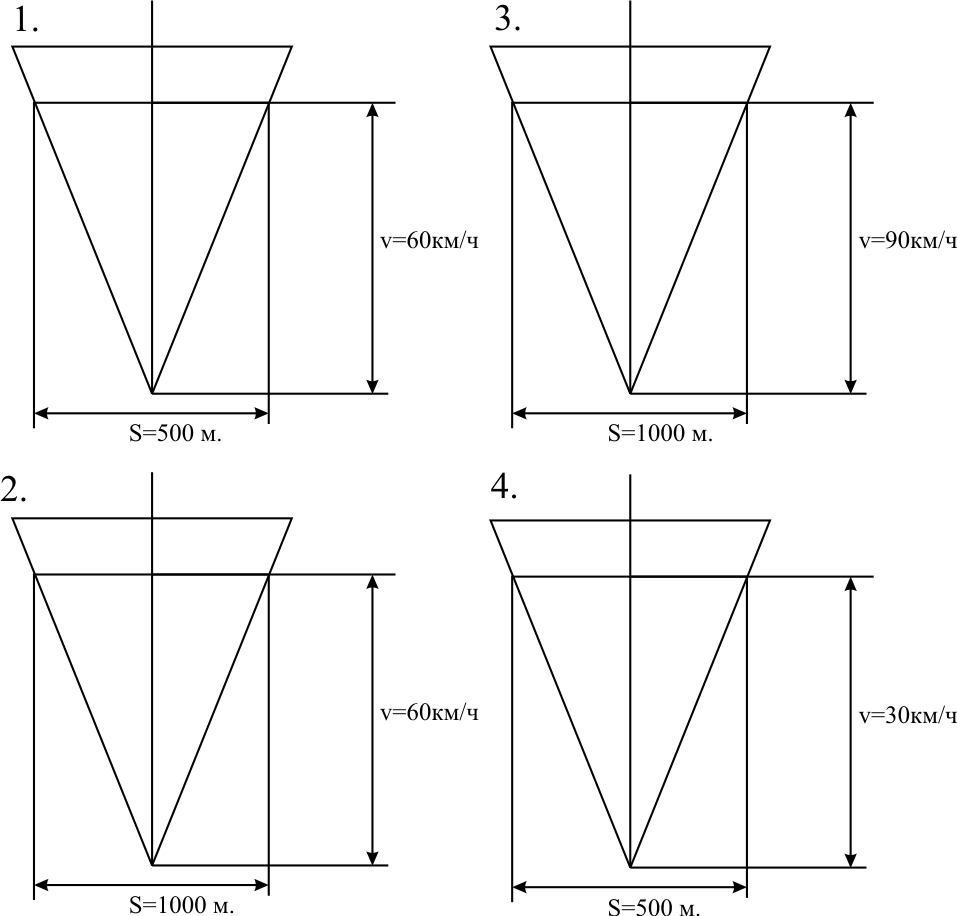 а) 1;3(+) б) 2;4 в) 0 1.3.2.6.4 На рисунке приведены треугольники времени, определите те треугольники, которые являются двухминутными. Необходимо указать все двухминутные треугольники. Если таких треугольников несколько, то ответ вводится через «;». Если таких треугольников нет, введите 0. 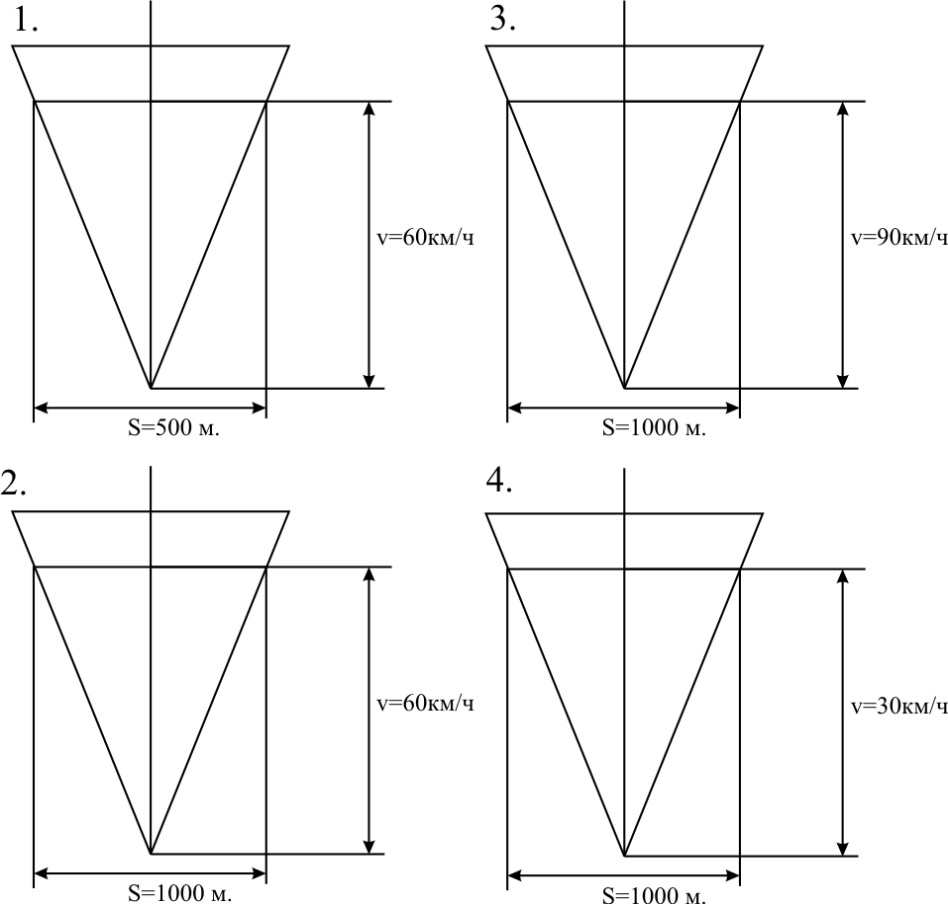 а) 0 б) 4(+) в) 3 1.3.2.6.5 На рисунке приведены треугольники времени, определите те треугольники, которые являются двухминутными. Необходимо указать все двухминутные треугольники. Если таких треугольников несколько, то ответ вводится через «;». Если таких треугольников нет, введите 0. 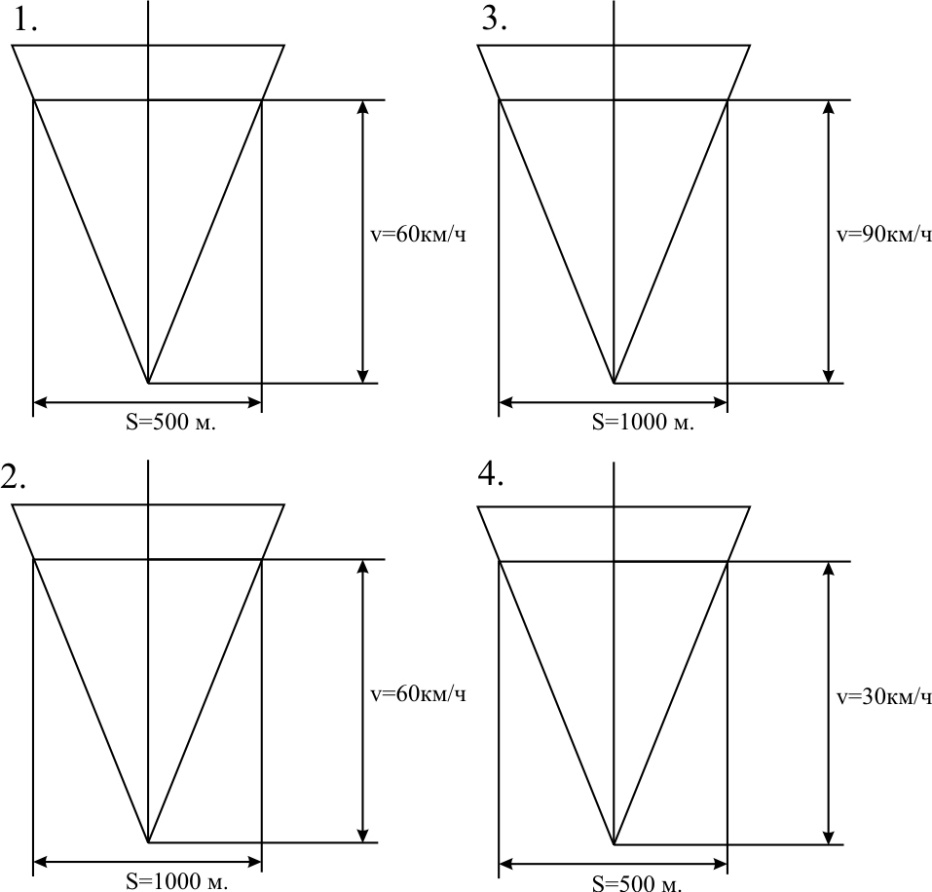 а) 0(+) б) 1 в) 3 1.3.2.6.6 На рисунке приведены треугольники времени, определите те треугольники, которые являются полуминутными. Необходимо указать все полуминутные треугольники. Если таких треугольников несколько, то ответ вводится через «;». Если таких треугольников нет, введите 0. 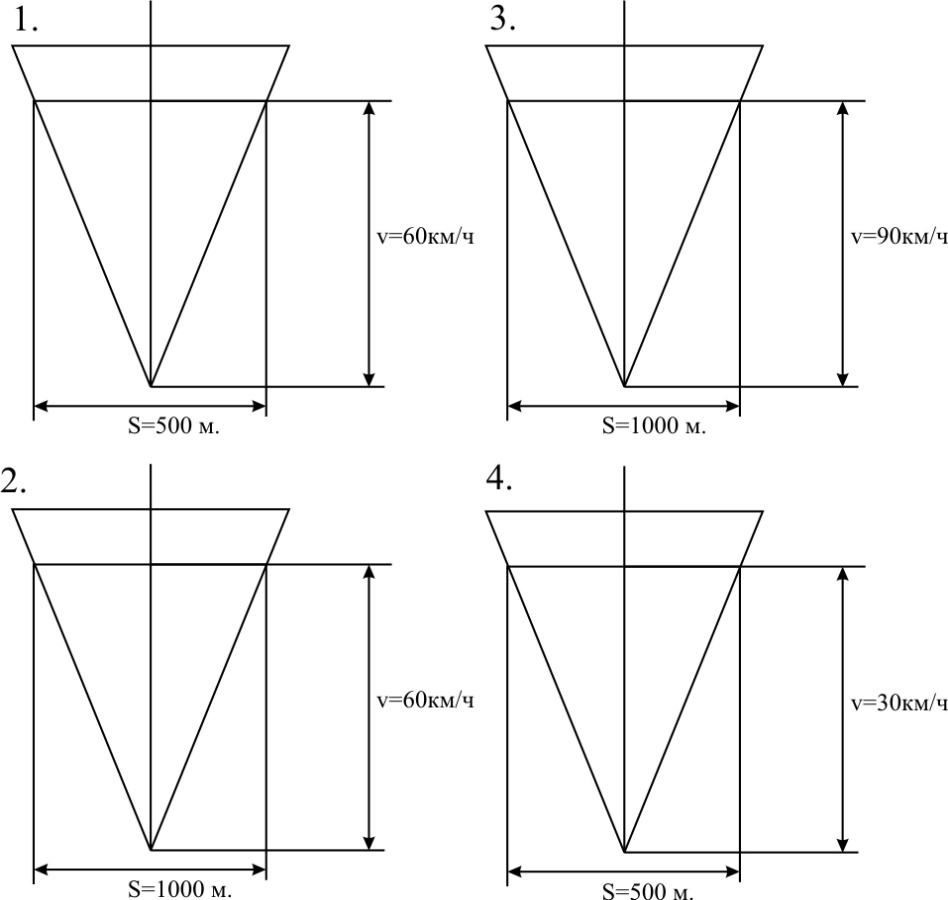 а) 2 б) 3 в) 1(+) 1.3.2.6.7 На рисунке приведены треугольники времени, определите те треугольники, которые не являются минутными. Необходимо указать все неминутные треугольники. Если таких треугольников несколько, то ответ вводится через «;». Если таких треугольников нет, введите 0. 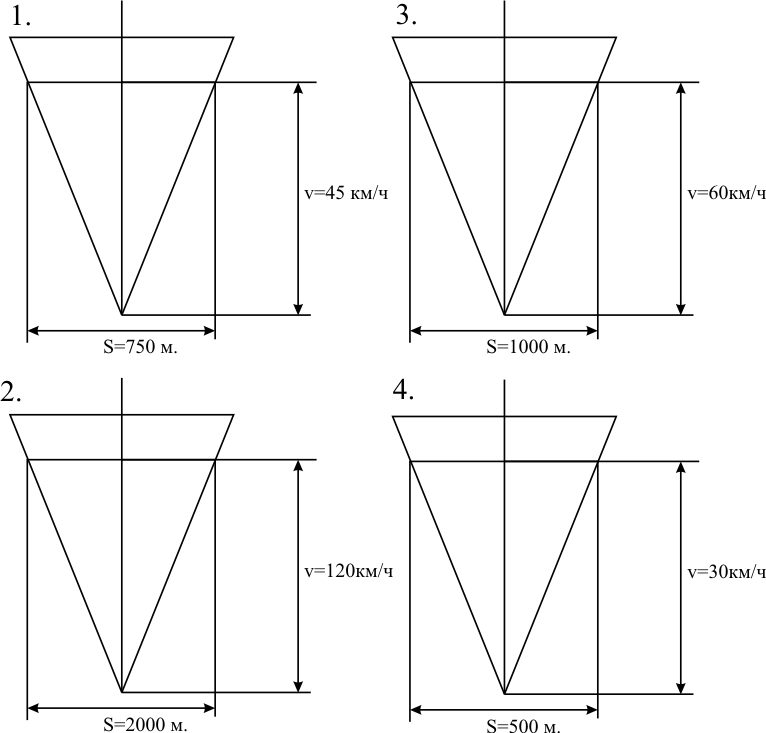 а) 4 б) 0(+) в) 2 1.3.2.7.1 При определении времени хода грузового поезда по участку методом равномерных скоростей три дополнительные минуты распределяются следующим образом: а) 1 мин. на разгон, 2 мин. на замедление; б) 2 мин. на разгон, 1 мин. на замедление; (+) в) 1,5 мин. на разгон, 1,5 мин. на замедление. 1.3.2.7.2 Величина равномерной скорости движения поезда лежит в пределах: а) от расчетной до допустимой; (+) б) от нуля до конструкционной; в) от автоматической до допустимой. 1.3.2.7.3 При определении времени хода пассажирского поезда по участку методом равномерных скоростей дополнительные минуты распределяются следующим образом: а) 1 мин. на разгон, 1 мин. на замедление; (+) б) 2 мин. на разгон, 1 мин. на замедление; в) 1,5 мин. на разгон, 1,5 мин. на замедление. 1.3.2.8.1 В основе определения времени хода поезда по участку методом равномерных скоростей лежат следующие допущения: а) поезд движется равноускоренно; б) поезд движется равнозамедленно; в) поезд движется равномерно.(+) 1.3.2.8.2 При определении времени хода поезда по участку методом равномерных скоростей предполагается, что на границах элементов скорость меняется следующим образом: а) плавно уменьшается; б) плавно увеличивается; в) мгновенно возрастает ;(+) г) мгновенно убывает.(+) |
