Методы_контроля_Командик (1). Ббк75. 1 я73 м 54 Рекомендовано к изданию Ученым советом Инновационного Евразийского университета Протокол 9 от

• Название: Ббк75. 1 я73 м 54 Рекомендовано к изданию Ученым советом Инновационного Евразийского университета Протокол 9 от
• Дата: 04.06.2022
• Размер: 4.61 Mb.
• Имя файла: Методы_контроля_Командик (1).docx
• Тип: Протокол; #569016
• страница: 46 из 58

Основные статистические характеристики ряда измерений

Наиболее часто в педагогических исследованиях бывает необходимо оценить динамику показателей, происходящую под влиянием каких-либо педагогических воздействий или естественную возрастную динамику развития учащихся при сравнении исходного и конечного уровня этих показателей в одной и той же группе (в последовательном эксперименте) или в параллельных группах (в сравнительном эксперименте). Для этого нужно иметь какие-то критерии, по которым можно было бы судить о достоверности различий в полученных количественных данных. Для установления достоверности различий прибегают к вычислению некоторых статистических показателей (параметров).

Основные статистические характеристики ряда измерений (вариационного ряда) это: объем выборки, средняя арифметическая величина, мода, медиана и вариация (разброс показателей в вариационном ряду).

1. Объем выборки

Одной из основных характеристик выборки является ее объем – n, который определяется числом объектов наблюдения, например, учащихся в данном исследовании.

Определить оптимальный объем выборки помогает знание некоторых общих положений.

1. 
   Число необходимых исследований зависит от вариативности (изменчивости) признака, характеризующего то или иное явление: чем она больше, тем большее количество исследуемых или измерений на каждом человеке потребуется. Например, показатель мышечной силы менее вариативнен, чем время двигательной реакции.
   
2. 
   Объем выборки заметно предопределяет получение достоверных результатов исследования, особенно при большом разбросе показателей изучаемого признака. Например, в одном и том же классе обучаются дети одного возраста, разница в длине тела которых может варьировать от 5 до 35 см и более. Это же можно сказать и о физических качествах, т.к. некоторые дети опережают своих сверстников в биологическом возрасте, а некоторые отстают. Так, в одном и том же 7 классе мальчики могут показать результат в прыжках в длину с места от 165 до 220 см.
   

Устанавливая количество исследуемых нужно придерживаться правила «чем больше, тем лучше». Однако практика показывает, что в педагогических исследованиях чаше всего используется формирование опытных групп численностью от 15 до 40 человек.

Если же речь идет о разработке возрастных стандартов и оценочных таблиц, тогда испытуемых должно быть несколько сотен каждого пола в каждой возрастной параллели.

2. Средняя арифметическая величина, мода, медиана

Центральную тенденцию выборки позволяют оценить такие статистические характеристики, как средняя арифметическая величина, мода, медиана.

Средняя арифметическая. Условное обозначение средней арифметической ^X . Средняя арифметическая величина является производной, обобщающей количественные признаки ряда однородных показателей (совокупности). Точность вычисления средней арифметической величины должна соответствовать содержанию изучаемого педагогического явления. В некоторых случаях нет необходимости в расчетах с большой точностью, в других - большая точность нужна в вычислениях, но совершенно не нужна в выводах. Например, при расчете средних величин числа подтягиваний на перекладине можно пользоваться и сотыми долями целого, но представлять в выводах числа, округленные до целых единиц.


В простейшем случае, для неупорядоченного ряда измерений, этот показатель вычисляется путем сложения всех полученных значений (которые называются вариантами) и деления их суммы на число вариант:


X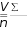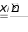
где: ∑- знак суммы; n - число вариант; V – полученные в измерениях значения (результаты выполнения задания каждым испытуемым - варианты). В педагогических исследованиях чаще встречается еще одно обозначение варианты - x_i, когда индекс i принимает значения от 1 до n (т.е. вместо индекса i можно подставить номер, под которым в вариационном ряду записан результат каждого испытуемого). Его называют индексом суммирования.





X
Например, при изучении результатов прыжка в длину с места в группе из 10 человек выражение ∑Хi будет пониматься так: Х₁+Х₂+Х₃…….+Х₁₀, где Х1, предположим, равно 175см, Х₂ = 190 см, Х₃ = 180 см…….Х₁₀ =175см).

Мода. Модойназывают результат выборки, наиболее часто встречающийся в этой выборке. Его обозначают символом Мо.

Медиана. Медиана- результат измерений, который находится в середине ранжированного ряда. Он обозначается символом Ме. Своё применение он находит в основном в спорте. Например, в некоторых видах спорта, где оценка спортсмену выставляется несколькими судьями (в гимнастике), самые высокие и самые низкие оценки отбрасываются, и в зачет идет медиана. Например, пять судей поставили 9.1, 9.1, 9.2, 9.3, 9.4 балла. Отбрасываются высшие и низшие оценки, и спортсмену выставляется 9.2 балла.

3. Характеристики вариации результатов измерений (размах, дисперсия, среднее квадратическое отклонение, коэффициент вариации)

Средняя арифметическая величина позволяет сравнить и оценить группы изучаемых явлений в целом. Однако для характеристики группы явлений только этой величины явно недостаточно, т.к. размер колебаний вариант, из которых она складывается (размер отклонения каждого результата от средней арифметической), может быть различным. Например: две группы школьников по 5 человек прыгнули в длину с места. Средняя арифметическая результатов в одной и во второй группе была равна 175 см. Однако в первой группе она получена из слагаемых 215 см + 205 см + 145 см + 155 см + 155 см; во второй группе 185 см + 185 см, +170 см + 175 см + 160 см. Можно ли сказать что скоростно- силовая подготовка этих групп школьников одинаковая? Для получения ответа на этот вопрос в характеристику группы явлений необходимо внести такой показатель, который давал бы представление о величине колебаний вариант около их средней величины (вариации).

К основным характеристикам вариации результатов измерений относят размах выборки, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Рассмотрим их подробнее.

Размах выборки. Размахвыборкиили размах варьирования определяется как разность между наибольшим и наименьшим результатами измерений. Так в приведенном выше примере в первой группе размах выборки будет таковым: 215 см – 145 см = 70 см; во второй группе: 185 см – 160 см = 25 см. Однако он улавливает только крайние отклонения, но не отражает отклонения всех результатов, поэтому не может быть единственной характеристикой вариативности ряда.

Дисперсия. Чтобы дать обобщенную характеристику вариации, можно вычислить отклонение каждого результата от средней величины, а затем суммировать их. Например, для ряда 3,6,3 среднее значение ^{будет равняться 4 (12 : 3). Тогда значения (Хi -} X^{) будут следующими:} 3 - 4 = -1; 6 – 4 = 2; 3 – 4 = -1. Сумма чисел этих отклонений равна 0.

Чтобы избежать этого, значение каждого отклонения возводят в квадрат: (-1)² + 2² + (-1)² = 1+4+1=6.

^{Значение (Хi -} X ^{)2 делает отклонения от средней более} явственными: малые отклонения становятся еще меньше (0,5² =0,25), а ^{большие еще больше (52 = 25). Получившуюся сумму ∑( Хi -} X ⁾² называют суммой квадратов отклонений. Разделив эту сумму на число измерений получают средний квадрат отклонений или дисперсию. Его условное обозначение σ². Он вычисляется по формуле:

2

₂ x_iX

n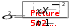
^{а при n 30}
Но чаще в исследованиях встречается другой параметр, среднееквадратическое отклонение, который определяется как положительное значение корня квадратного из значения дисперсии.

Среднее квадратическое отклонение. Этот статистический параметр называется еще стандартнымотклонениемили просто стандартом. Условное его обозначение – σ (сигма). Величина среднего квадратического отклонения является показателем рассеивания (т.е. отклонений вариант, которые получены в исследовании, от их средней арифметической величины) и призвана дополнять характеристику группы явлений.

Стандартное отклонение имеет те же единицы измерения, что и измеряемые показатели.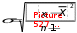


В тех случаях, когда объем выборки очень большой, чтобы избежать большого количества расчетов, среднее квадратическое отклонение –σ можно рассчитать другим, более удобным в данном случае способом (Н.А. Толоконцев - 1961):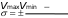
K

где V max. - наибольшее значение варианты, V min. - наименьшее значение варианты,

К - табличный коэффициент, соответствующий определенной величине размаха.

Коэффициент К определяется по «Таблице коэффициентов К для вычисления среднего квадратического отклонения по амплитуде вариационного ряда» (Приложение А).

Величина среднего квадратического отклонения зависит от величины колебания вариант: чем больше амплитуда различий между крайними значениями вариант, т.е. чем больше изменчивость признака, тем больше величина среднего квадратического отклонения.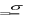

Коэффициент вариации. Стандартное отклонение измеряется в тех же единицах, что и измеряемый показатель. Однако для сравнения колеблемости двух и более совокупностей, имеющих разные единицы измерения, эта характеристика не пригодна, для этого используют коэффициент вариации. Он определяется как отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах. Вычисляется он по формуле:

V.10%0

X

В спортивной практике колеблемость результатов измерений в зависимости от величины коэффициента вариации считают небольшой от 0 до 10%; средней – от 11 до 20% и большой от 20% и более. Коэффициент вариации можно использовать только в том случае, если измерения выполнены в шкале отношений.

4. Вычисление средней ошибки средней арифметической

Условное обозначение среднейошибкисредней арифметической величины m. Следует помнить, что под «ошибкой» в статистике понимается не ошибка исследования, а мера представительства данной величины, т.е. мера, которой средняя арифметическая величина, полученная на выборочной совокупности, отличается от истинной средней арифметической величины, которая была бы получена на генеральной совокупности. Ответ на этот вопрос и дает вычисление средней ошибки среднего арифметического, которое производится по формуле: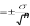

m

3. Закон нормального распределения вариант

Закон нормального распределения гласит:

в однородной группе вариант больше всего значений встречается в интервале, расположенном около средней арифметической величины (в интервале ^Х± 1σ). На рисунке 73 видно, что в интервале от -1σ до

+1σ находится 68,26% вариант;

чем больше отличается каждая отдельная варианта от средней арифметической величины, тем она реже встречается. Так, в интервалах от -1σ до - 2σ и от + 1σ до + 2σ расположено с каждой

стороны по 13, 56% , что в сумме составляет 27,12%. В интервалах от

-2σ до - 3σ и от + 2σ до + 3σ находится, соответственно, только 4,28% вариант и т.д.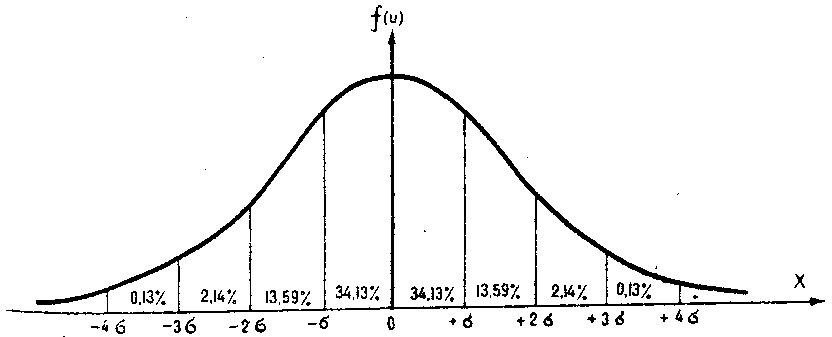

варианты меньше, чем средняя арифметическая величина, встречаются примерно с той же частотой, что и варианты больше, чем средняя арифметическая величина. На рисунке 73 видно, что в диапазоне от 0 до - 4σ и 0 до + 4σ располагается равное количества вариант.



Рисунок 73. Кривая нормального распределения чисел

Для оценки варьирования результатов измерений придерживаются следующих соотношений:

интервал _Х± 1σ включает 68,27 % всех полученных результатов; ^{интервал} Х^{± 2σ включает 95.45 % всех полученных результатов;} интервал _Х± 3σ включает 99.73 % всех полученных результатов;

4. Проверка статистических гипотез с помощью параметрических критериев

1. 
   Формулировка статистических гипотез
   

Статистической гипотезой называется проверяемоематематическими методами предположение относительностатистических характеристик результатов измерений. Статистическую гипотезу обычно обозначают знаком Н - (утверждение). Предположим, что в двух группах студентов происходило обучение стрельбе по двум методикам. Таким образом: имеется средняя арифметическая величина, отражающая результаты измерений точности стрельбы в группе «А», где обучение

проводилось по новой методике. ^Х_А = 5,6 см. В группе «Б» обучение проводилось по традиционной методике. Предположим,

что средняя арифметическая проведенных измерений в группе - ^Х_Б


= 4,7 см. Очевидно, что ^Х_А > ^Х_Б на 0,9 см. Если на основании этого мы предполагаем (выдвигаем статистическую гипотезу), что в результате обучения по новой методике студенты группы «А» стали

стрелять лучше, то гипотеза (утверждение) запишется как Н: ^ХА >

^Х Б. или ^Х Б < ^Х _А. Если мы предположим, что в полученных результатах нет достоверной статистической разницы, и отличие одной средней арифметической от другой случайное, то гипотеза

записывается как Н₀: ^Х_А = ^Х_Б (нулевая гипотеза).

При сравнении статистических характеристик двух выборочных совокупностей почти никогда не встречается случая их абсолютного равенства. В силу каких-то случайных или закономерных причин значения их отличаются друг от друга. Задача при проверке гипотез состоит в том, чтобы отличить случайные величины от закономерных.

Гипотеза никогда не бывает доказана на 100 %. Т.е. всегда случайные факторы вносят в результаты определенную погрешность. (Например: из 100 испытуемых, занимавшихся по экспериментальной методике силовой подготовкой у 95 % занимавшихся результаты улучшились, а у 5 % в силу каких-то причин остались на прежнем уровне или ухудшились). Оценка степени этой погрешности и представляет собой суть проверки статистической гипотезы. Для ее обозначения вводится такой показатель как уровеньзначимости(α), который характеризует вероятность доказательства гипотезы или с другой стороны – степень внесения погрешности в доказательство гипотезы в силу случайных причин. Существует три уровня доказательства гипотез: 0,001; 0,01; 0,05. Чем он меньше, тем выше степень доказательства гипотезы. Если бы в доказательство гипотезы не вмешивались случайные факторы, то при подтверждении гипотезы α равнялся бы

1. 
   Т.е. гипотеза подтверждалась бы на 100 %. Уровень 0,05 означает, что числовые значения (результаты измерения), не подтверждающие гипотезу могут встретиться в среднем не чаще, чем 5 раз в 100 наблюдениях (т.е. в 5%наблюдений).
   

Величину q=1–αназываютдоверительнойвероятностью(при уровне значимости – 0,05 доверительная вероятность равна 0,95, т.е полученным данным можно доверять на 95%.

Как принятие, так и отклонение гипотезы осуществляется на основе определенного критерия. Статистическимкритериемназываютправило,обеспечивающеепринятиеистиннойилиотклонениеложнойгипотезысзаранеезаданнойвероятностью.В педагогических исследованиях при изучении явлений, измеренных с помощью приборов с вычислением каких-либо параметров (граммов, сантиметров, количества раз и пр.), т.е.

данные получены в с помощью шкалы отношений и интервальной шкалы, чаще всего используют t – критерий Стьюдента

Основными этапами проверки статистической гипотезы являются:

1. 
   этап – формулировка гипотезы относительно средних арифметических величин сравниваемых выборочных совокупностей, которую в дальнейшем необходимо принять или
   

отклонить. (Например: Н₀: ^Х_А = ^Х_Б);

2. 
   этап - выбор уровня значимости (α). (Например: α = 0,05);
   
3. 
   этап - расчет статистических характеристик вариационных рядов ( ^Х, σ, m);
   
4. 
   этап – расчет значения t_{расчетное} по формуле см. 4.4.2;
   
5. 
   этап - сравнение расчетного значения t с критическим значением критерия для выбранного уровня значимости (по таблице. Приложение Б) и принятие или отклонение гипотезы.
   
6. 
   этап – формулировка методического вывода.
   

2. Сравнение двух средних арифметических несвязанных выборочных совокупностей

При сравнении двух выборочных средних арифметических не связанных между собой выборок (т.е. два ряда чисел получены при обследовании испытуемых разных групп) необходимо убедиться, что они относятся к одной генеральной совокупности и, следовательно, существенно не отличаются друг от друга. Для их сравнения должны

быть известны ^Х₁ и ^Х₂, n₁ и n_2, σ₁ и σ₂, m₁ и m₂

В начале записывается гипотеза: предположим Н: ^Х ₁ < ^Х _2. Далее вычисляется значение критерия t расчетное и число степеней свободы. (Под числомстепенейсвободыпонимают разность между числом измеряемых значений и числом линейных отношений (связей), возникающих между ними. В некоторых литературных источниках встречается его обозначение буквами С, ν или n'. Оно рассчитывается так: n₁ + n₂ - 2)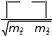

В независимых выборках t расчетное рассчитывается так:



Х₁ Х₂



t расчетное =
Обратите внимание, что выражение ^Х ₁ - ^Х ₂ заключено в две вертикальные черты, это означает, что в расчет берется его абсолютная величина, без знака «плюс» или «минус».

После того как вычислено значение t расчетное, его сравнивают с критическим значением t. Для этого пользуются таблицей теоретического распределения Стьюдента (Приложение Б) и для уровня значимости α и числа степеней свободы ν выписывают соответствующее значение t табличное.

Сравнивая значение t расчетное и t табличное поступают следующим образом. Если t расчетное < t табличного, гипотеза Н: ^Х₁ < ^Х_2.

отклоняется с вероятностью q = 1 – α; если t расчетное ≥ t табличному,

гипотеза Н: ^Х₁ < ^Х_2. принимается с вероятностью q = 1 – α.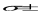

В виде примера можно рассмотреть исследование, в котором оценивалась разница в величине становой динамометрии боксеров двух весовых категорий. Были получены следующие исходные данные: тяжелый вес – n₁ = 12 человек, легкий вес - n₂ = 15 человек

X₁ 13.29

₁ 4.2кг

m₁ 1.23


X₂ 13.0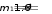

ν (число степеней свободы) = 12 + 15 – 2 = 25;

t _{расчетное} находится по формуле: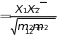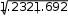

_t 139.2 135.0
=