Методы_контроля_Командик (1). Ббк75. 1 я73 м 54 Рекомендовано к изданию Ученым советом Инновационного Евразийского университета Протокол 9 от

• Название: Ббк75. 1 я73 м 54 Рекомендовано к изданию Ученым советом Инновационного Евразийского университета Протокол 9 от
• Дата: 04.06.2022
• Размер: 4.61 Mb.
• Имя файла: Методы_контроля_Командик (1).docx
• Тип: Протокол; #569016
• страница: 47 из 58

2.056

Полученное значение t сравним с граничным значением t –критерия Стьюдента по таблице (Приложение Б).

Для того чтобы определить значение t –критического (табличного) необходимо в соответствующей (левой) колонке таблицы найти число степеней свободы (ν). В нашем случае ν = 12 + 15 - 2 = 25. Далее, в строке, соответствующей числу степеней свободы, рассмотреть табличные значения t при разных уровнях значимости: 0,05, 0,01, 0,001 (т.е. при 5%, 1% или 0.1% вероятности ошибки).

В нашем примере по таблице, для числа степеней свободы (ν) = 25, граничное значение t при α -0,05 будет равняться 2,06, Как видим, t расчетное незначительно меньше t критического, что указывает на отсутствие достоверности различий (Р>0,05), где Р – вероятность ошибки. Однако незначительная их разница дает основание все таки предполагать наличие достоверной разницы в величине становой динамометрии боксеров двух весовых категорий. И при увеличении выборки она может быть доказана.

В тех случаях, когда расчеты показывают отсутствие достоверности различия, преждевременно считать, что между изучаемыми явлениями вообще их не может быть. Можно лишь утверждать, что нет различия при данных условиях исследования. При увеличении объема выборки достоверность различий может появиться. Это положение является главным доказательством важности правильного определения необходимого числа исследований до начала эксперимента.

3. Сравнение двух средних арифметических связанных выборочных совокупностей

В спорте и в школьном физическом воспитании часто на одних и тех же спортсменах или учащихся проводятся измерения через некоторое время в целях контроля динамики показателей какого-либо состояния занимающихся (до и после этапа тренировки, до и после учебного года и пр.) В таких случаях выборки на первом и на других этапах измерений равночисленны, а все измерения могут быть объединены в пары (каждая пара – это результаты измерений на одном человеке в начале и в конце эксперимента). Подобные выборки называются связанными(иликоррелированными).

В случаях связанных выборок не совсем корректно использовать методы, описанные ранее. В данном случае расчеты производятся следующим образом:

1. 
   Для каждого испытуемого определяется разность («сдвиг») между результатами первого и второго измерения, которая обозначается d_i. Например, если в начале учебного года ученик показывал результат в прыжках в длину с места 170 см, а в конце 185 см, то d = 185 – 170 = 15 см;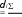
   
2. 
   Рассчитывается сумма и средняя арифметическая разностей:
   

X

d _n

3. 
   Рассчитывается среднее квадратическое отклонение разностей по формуле: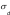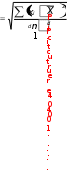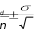
   

и стандартная ошибка средней разности

m_d.

4. 
   Рассчитывается критерий достоверности различий t:
   

^t расчетное ⁼

; ν = n – 1


X_d

m
d

где ^Х _d – средняя арифметическая разности, m_{d –} стандартная ошибка средней арифметической разности, ν – число степеней свободы;

5. 
   Сравнивается t расчетное с табличным значением t-критерия Стьюдента для уровня значимости α и ν = n – 1 (Приложение Б); подтверждается или опровергается выдвинутая статистическая гипотеза. При t расчетном ≥ t табличному гипотеза подтверждается с вероятностью q = 1 – α.
   

Как производятся расчеты на одной и той же группе испытуемых, можно рассмотреть на следующем примере. В подготовительном периоде тренировки в команде «A» (n = 10) проведена определенная работа для повышения выносливости спортсменов. В начале этого периода и позже повторно был измерен ИГСТ. Полученные результаты приведены в таблице 20. При анализе этих результатов необходимо выяснить, оказались ли средства повышения выносливости эффективными, т.е. достоверным ли является прирост выносливости. Сопоставляя отдельные результаты, видно, что у пяти спортсменов индекс повысился, у двух остался на прежнем уровне, а у трех снизился. Средняя арифметическая величина ИГСТ при повторном обследовании команды оказалась больше на 2 единицы. Если ограничиться только сопоставлением средних величин и абсолютных результатов, то может показаться, что выносливость в команде несколько улучшилась. Обратимся, однако, за более точным ответом к статистике. В данном случае оба цифровых ряда взаимно связаны друг с другом (повторное измерение в той же команде). Поэтому t рассчитывают следующим способом:

1. 
   Сначала определяют разницу между индивидуальными вариантами каждого спортсмена - X_d (см. среднюю колонку в таблице 20).
   
2. 
   Рассчитывают среднюю арифметическую величину цифровых рядов первого и второго обследования; в нашем примере они равны 84,5 и 86,5.
   
3. 
   Рассчитывают разность средних результатов, которая в то же время является средней арифметической разностей: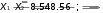
   

4. 
   ^{Производят расчеты (Хdi -} X_d^{) и (Хdi -} X_d^{)2 (см. таблицу).}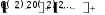
   
5. 
   ^{Рассчитывают сумму квадратов разностей - Σ(Хdi -} X_d^{)2 :}
   

1 ( 2) ²

( 4)²

2² … 1²

410;

Таблица 20 – Индекс Гарвардского степ-теста у представителей команды А в начале и в конце подготовительного периода

№	1 обследование	2 обследование	Сдвиг	Хdi- Xd	(Хid- Xd)2
1	79	85	-6	-4	16
2	89	89	0	-2	4
3	83	85	-2	0	0
4	81	81	0	-2	4
5	81	84	-3	-1	1
6	86	84	+2	4	16
7	90	82	+8	10	100
8	80	90	-10	-8	64
9	92	100	-8	-6	36
10	84	85	-1	1	1
	Х1= 84.5	Х2= 86.5	Хd= -2		∑ =242

6. 
   Рассчитывают среднее квадратическое отклонение разностей по формуле: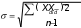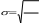
   

_; 410

9

= 6.75;

7. 
   Величину средней ошибки рассчитывают по формуле: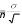
   

m

2.1
_m= 6.756.75 _;

10^3.16

8. 
   Вычисляют показатель статистической достоверности различий t по формуле:
   

X

t расчетное = d

m_d

= ² = 0,94.

2.13

9. 
   Сравнивают расчетный показатель с табличным (см. приложение Б). Степень свободы (ν) в данном случае равна n – 1 = 9.
   

Как видно из таблицы, для доказательства достоверности различий расчетный показатель t должен равняться или превышать 2,26. при уровне значимости α = 0,05. Вычисленный же нами показатель t

расчетное равен 0,94, что намного меньше табличного показателя (Р>0,05), Это значит, что увеличение индекса Гарвардского степ-теста у нескольких спортсменов при повторном обследовании имеет случайный характер, и использованную в команде методику тренировки для развития выносливости нельзя признать более эффективной.