Методы_контроля_Командик (1). Ббк75. 1 я73 м 54 Рекомендовано к изданию Ученым советом Инновационного Евразийского университета Протокол 9 от

• Название: Ббк75. 1 я73 м 54 Рекомендовано к изданию Ученым советом Инновационного Евразийского университета Протокол 9 от
• Дата: 04.06.2022
• Размер: 4.61 Mb.
• Имя файла: Методы_контроля_Командик (1).docx
• Тип: Протокол; #569016
• страница: 49 из 58

Случай построения многопольной «таблицы»

Применение критерия χ² возможно и в том случае, когда результаты групп, сравниваемых по состоянию изучаемого свойства, признака, рас- пределяются более чем на две категории. В этих случаях для вычисления достоверности различий строятся многопольные «таблицы». Например, мы хотим сравнить эффективность проведения профориентационной работы среди учащихся выпускных классов, задача которой – агитация выпускников за поступление на факультет физической культуры. Для этой цели отберем две равноценные группы учащихся средних школ. В одной из них – экспериментальной (n= 100 чел.) работа ведется непосредственно преподавателями и студентами факультета путем проведения бесед, лекций, экскурсий, также через периодическую печать и радио; в другой - контрольной (n=100 чел.) – только через периодическую печать и радио. Результаты проведения такой работы проверим с помощью анкеты. Ответы учащихся на вопросы анкеты можно подразделить на три категории типа: «Хочу поступать на факультет физической культуры», «Не хочу» и

«Не знаю».

Проверяется гипотеза, что профориентационная работа в экс- периментальных школах окажется более эффективной, и у учеников этих школ ответов «хочу поступать» будет достоверно больше, чем у учеников контрольных школ.

При построении многопольной таблицы результаты измерения состояния изучаемого свойства каждой группы распределяются на С категорий. На основе данных составляется «таблица» 2 х С, в которой два ряда - по числу рассматриваемых групп и С колонок - по числу различных категорий состояния изучаемого свойства, принятых в исследовании (таблица 23).
Таблица 23 – Многопольная таблица для расчета критерий χ²

	Категория 1	Категория 2		Категория i		Категория С
Эксперимен- тальная группа	Э1	Э2		Эi		Эс
Контрольная группа	К1	К2		Кi		Кс
	Э1+ К1	Э2 + К2		Эi + Кi		Эс + Кс

В этой «таблице» Э_i (i = 1, 2, ...до С) – число испытуемых экспе- риментальной группы, попавших в i-ю категорию по состоянию изучаемого свойства; Кi (i = 1, 2, ...до С) – число испытуемых конт- рольной группы, попавших в i-ю категорию по состоянию изучаемого свойства. Для проверки рассмотренной выше гипотезы с помощью критерия хи-квадрат на основе данных «таблицы» 2 х С рассчитывается значение статистического (наблюдаемого) критерия по следующей формуле: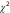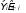

₁ (n_ýK_i n_êÝ_i)²



n_ýn_ê

Рассчитанное по этой формуле значение χ², полученное на основе экспериментальных данных, сравнивается с критическим значением (χ²_крит) которое определяется по таблице (Приложение В) с степенью свободы С – 1 для 5%-ного уровня значимости. Если мы получим значение хи-квадрат, которое будет больше критического значения (χ²_{расчетн} > χ²_крит,), то это значит, что большее число ответов «хочу поступать» у учащихся экспериментальных школ не является случайностью и, стало быть, можно говорить о преимуществах

расчетн
экспериментальной работы. В случае, когда χ²

< χ²

крит

, т.е. эти

различия считаются недостоверными, имеют случайный характер, поэтому признавать эту работу более эффективной нет оснований.

Предположим, что в нашем примере ученики экспериментальных школ (100 чел.) распределились в зависимости от своих ответов на вопросы анкеты следующим образом: «Хочу» – 40; «Не хочу» – 35; «Не знаю» — 25, а ученики контрольных школ (100 чел.) соответственно 20; 45 и 35. На основе этих данных составим многопольную таблицу 24:
Таблица 24 – Исходные данные для расчета критерий χ² с помощью многопольной таблицы

	«Хочу»	«Не хочу»	«Не знаю»
Эксперимен- тальная группа	Э1 = 40	Э2 = 35	Э3 = 25	nэ = 100
Контрольная группа	К1 = 20	К2 = 45	К3 = 35	nк = 100
	Э1 + К1 = 60	Э2 + К2 = 80	Э3 + К3 = 60	N = 200

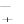расчетн:
По формуле рассчитаем значение χ²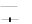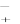

₂ 1 (nКnЭ)² (nКnЭ)²

(nКnЭ)²

э1к1 ₊ э2 к2

₊ э3 К3 ₌

n_эn_к

Э₁ К₁

Э₂ К₂

Э₃ К₃

По таблице (Приложение В) находим критическое значение (χ²_крит) для числа степеней свободы V= С-1 = 3-1 = 2 при уровне значимости α= 0,05. Оно равно 5,99, что меньше расчетного значения. Отсюда верно

расчетн
неравенство χ²

> χ²

крит

, (9,58 > 5,99), что свидетельствует о

достоверности различий между ответами учащихся экспериментальной и контрольной групп. Таким образом подтверждается наша гипотеза о том, что экспериментальная работа по профориентации была более эффективной по сравнению с информацией, которую учащиеся получали из СМИ, (Р < 0,05, т.е. вероятность ошибки меньше 5%).

Глава 5. ВЗАИМОСВЯЗЬ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. 
   Функциональная и статистическая взаимосвязь
   

В любом педагогическом процессе составляющие его факторы находятся в тесной взаимосвязи. Умение изменить один фактор так, чтобы получить соответствующее значение другого, делает педагогический процесс более целенаправленным. В науке различают две формы взаимосвязи.

Функциональная связь выражает четкую однозначную зависимость, при которой изменение какого-либо одного фактора неизбежно приводит к однозначному изменению другого. Подобные связи характерны для «точных» наук. В педагогике они, если и наблюдаются, то в самых общих вариантах и в пределах каких-то условных границ.

Более реальным является установление так называемых статистическихсвязей, или корреляций.Статистический метод, который используется для исследования взаимосвязей, называется корреляционныманализом. Основной задачей его является определение формы, тесноты и направленности взаимосвязей изучаемых показателей.

Практическая значимость определения величины и характера корреляции в физическом воспитании заключается в том, что с ее помощью можно установить функциональное сходство или различие между физическими упражнениями, например общеподготовительными и соревновательными. Однако, применяя корреляцию, следует помнить, что, во-первых, наличие статистической связи отнюдь не означает автоматического выявления и причинных связей, поэтому использовать корреляционный анализ для понимания причинных факторов надо осторожно; во-вторых, нельзя механически применять корреляцию там, где по природе своей педагогические факторы не обладают зависимостью.

Коррелирующие факторы подразделяются на причинные,т.е. те, которые видоизменяются первыми, вызывают изменение других

факторов, и следственные,т.е. те, которые видоизменяются под влиянием причинных факторов. Причем следственные факторы могут принимать ряд значений в определенных границах.

2. Направленность и теснота взаимосвязи

Различают корреляции нескольких направлений:

прямаяположительнаякорреляция, при которой увеличение причинного фактора вызывает увеличение следственного фактора; например, увеличение силы разгибателей ног положительно сказывается на росте результатов в прыжках в высоту с разбега;

прямаяотрицательнаякорреляция, при которой уменьшение причинного фактора вызывает уменьшение следственного фактора; например, уменьшение нагрузки вызывает понижение частоты сердечных сокращений;

обратнаяположительнаякорреляция, при которой уменьшение причинного фактора вызывает увеличение следственного фактора; например, уменьшение длины дистанции приводит к увеличению скорости бега;

обратнаяотрицательнаякорреляция, при которой увеличение причинного фактора вызывает уменьшение следственного фактора; например, увеличение силы мышц под влиянием занятий тяжелой атлетикой может привести к ухудшению результатов в беге на длинные дистанции и гибкости.

Математическое значение корреляции выражается ее коэффициентом от -1 (максимальной отрицательной связи) до +1 (максимальной положительной связи) десятичными дробями с точностью до второго знака после запятой.

Количественную меру связи принято различать по нескольким уровням:

слабаясвязь- при коэффициенте корреляции до 0,30

средняясвязь- при коэффициенте корреляции от 0,31 до 0,69,

сильнаясвязь- при коэффициенте корреляции - от 0,70 до 0,99.

Коэффициент корреляции равный 1 свидетельствует о наличии функциональной связи. Если изменение одного фактора не влияет на величину другого, то связь отсутствует, т.е. данные факторы между собой нейтральны. Тогда коэффициент корреляции равен 0.

3. Методы вычисления коэффициентов взаимосвязи

   1. 
      Ранговая корреляция Спирмена
      

Корреляция рангов (ее обозначают буквой ρ) является одним из наиболее простых способов установления связи между факторами. Само название метода указывает на то, что связь определяется между рангами, т.е. рядами полученных количественных значений, ранжированных в убывающем или возрастающем порядке.

При применении метода ранговой корреляции следует иметь в виду, что, во-первых, ранговую корреляцию не следует вводить, если связанных пар меньше четырех и больше двадцати; во-вторых, ранговая корреляция позволяет установить связь и в том случае, если измерения проведены в шкале порядка; например – места, занятые спортсменами на соревнованиях; в третьих, ранговую корреляцию целесообразно применять в тех случаях, когда достаточно получить лишь приблизительную информацию.

Рассмотрим механизм расчета коэффициента ранговой корреляции на примере.

Чтобы рассчитать коэффициентранговойкорреляции(ρ), необходимо:

1. 
   расположить количественные значения причинного фактора в убывающем (возрастающем) порядке; например, для установления влияния уровня физической работоспособности лыжников (причинный фактор), выявленного при помощи дозированной нагрузки на велоэргометре, на результат в гонке на 15 км (следственный фактор). Уровень физической работоспособности ранжировался в убывающем порядке (результаты отображены в колонке «А», таблица 25);
   
2. 
   параллельно первому ряду записать соответствующие значения следственного фактора, в данном случае - результаты в гонке на 15 км (колонка «Б); порядок значений этого фактора будет подчинен порядку значений причинного фактора (т.е. результату каждого спортсмена на велоэргометре – колонка А - соответствует его результат в гонке – колонка Б), а поэтому может не подчиняться принципу возрастания или убывания;
   
3. 
   обозначить цифрами порядковые места значений причинного фактора (колонка «а»). Естественно, что раз значения этого фактора расположены в убывающем порядке, то цифры порядковых мест будут расположены в возрастающем порядке; если количественные показатели того или иного фактора оказываются одинаковыми (т.е. два или три спортсмена показали одинаковый результат в гонке), то их порядковые места обозначаются тем числом, которое составляет среднюю арифметическую величину их порядковых мест;
   
4. 
   обозначить цифрами порядковые места значений следственного фактора (колонка «б»);
   
5. 
   подсчитать число коррелируемых парных значений (n); в данном примере их 10;
   
6. 
   вычислить разность рангов (d = а - б) с сохранением соответствующего знака; в данном примере: 1 - 2 = -1 и т.д.;
   
7. 
   вычислить квадрат разности рангов (d²); в данном примере: -1² = 1 и т.д.;
   
8. 
   вычислить сумму квадратов разности рангов; в данном примере
   

∑d² = 32;

Таблица 25 – Зависимость результатов в гонке на 15 км от уровня физической работоспособности

РWC170 (КГм/ми н/кг)	Результат гонки, (мин)	Ранги РWC170		Результат	Разность рангов	Квадрат разности рангов
A	Б	а		б	d = a - b	d2
24,08	63	1		2	-1	1
24,2	61	2		1	+1	1
24,0	72	3		5	-2	4
20,4	71	4		4	0	0
20,1	70	5		3	+2	4
19,0	82	6		10	-4	16
17,5	77	7		7	0	0
17,2	75	8		6	+2	4
16,8	79	9		8	+1	1
16,3	81	10		9	+1	1
n=10			∑d2 = 32

9. 
   вычислить коэффициент корреляции рангов ρ по формуле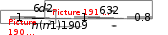
   

10. 
    произвести оценку вычисленного коэффициента.
    

Значимость коэффициента корреляции рангов определяется двумя путями:

а) путем сравнения с принятыми уровнями меры количественной связи (об этом говорилось выше); в данном примере величина коэффициента корреляции, равная 0,807, это свидетельствует о сильной мере количественной связи;

б) по таблице достоверности коэффициента корреляции (Приложение Г). Коэффициент корреляции рангов признается статистически значимым с вероятностью ошибки меньше 5 %, если его величина будет превышать табличное значение для соответствующего количества парных наблюдений в колонке α - 0,05, (т.е. Р < 0,05), и с вероятностью ошибки меньше 1 %, если его величина будет превышать табличное значение для соответствующего количества парных наблюдений в колонке α - 0,01, (т.е. Р < 0,01). Рассчитанный коэффициент, равный 0,807, может быть признан значимым в том случае, если его величина будет превышать табличное значение для 10 парных наблюдений. В таблице для 10 пар при уровне значимости α - 0,05 он равен 0,564 и α - 0,01 он равен 0,746. Следовательно, 0,564 < 0,807 > 0,746, т.е. рассчитанный коэффициент превышает табличный

при α - 0.01 и может считаться значимым с вероятностью ошибки Р < 0,01;

11. 
    сделать методический вывод, т.е. выяснить внутренний смысл высчитанного коэффициента корреляции. В приведенном примере можно убежденно говорить, что среди прочих условий на результат в лыжной гонке оказывает существенное влияние уровень физической работоспособности спортсменов.
    

2. Парный линейный коэффициент корреляции Бравэ- Пирсона

Коэффициент корреляции Бравэ-Пирсона обладает более высокой степенью точности количественной оценки связи между факторами. Он является показателем тесноты взаимосвязи и используется тогда, когда измерения производят в шкале отношений или интервалов и форма взаимосвязи линейная. Обозначается он латинской буквой – r.

Расчет коэффициента г производится по формуле: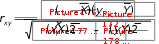




где X и Y - коррелируемые ряды вариант, (x_i - _X ) и (y_i -_Y ) отклонения вариант от срединных значений этих рядов (разность между каждым значением варианты ряда и средней арифметической величиной данного ряда). Точность, вычисленная по формуле должна быть достаточно высокой, не менее двух знаков после запятой.

Последовательность вычисления коэффициентаг можно продемонстрировать на примере результатов исследования, использованных для расчета коэффициента ранговой корреляции Спирмена;

1. 
   Составить таблицу для первичных операций (см. таблицу 26), для чего в первых двух колонках расположить показатели уровня физической работоспособности (PWC₁₇₀) и соответствующие им показатели спортивного результата в гонке на 15 км; ранжирование показателей не обязательно;
   

Таблица 26 – Зависимость результатов в гонке на 15 км от уровня физической работоспособности

PWC170 кГм/мин/кг	Результат гонки, мин	(xi- X)	(yi-Y)	(xi- X)2	(yi-Y)2	(xi- X) · (yi-Y)
Х	Υ
24,8	63	+4,8	-10	23,04	100	-48,0
20,1	70	+0,1	-3	0,01	9	-0,3
20,4	71	+0,4	-2	0,016	4	-0,8
24,0	72	+4,0	-1	16,00	1	-4,0
17,5	77	-2,5	+4	6,25	16	-10,0
16,8	79	-3,2	+6	10,24	36	-19,2
19,0	82	-1,0	+9	1,00	81	-9,0
17,2	75	-2,8	+2	7,84	4	-5,6
24,2	61	+4,2	-12	17,64	144	-48,4
16,3	81	-3,7	+8	16,69	64	-29,6
∑ x =200,3	∑ y =73,1			∑(xi- X)2 ≈ 96	∑(yi-Y)2 = 459	∑(xi- X) · (yi-Y) ≈175
X= 20.0	Y= 73.1

2. 
   Вычислить средние арифметические величины для уровня работоспособности и результата гонки:
   

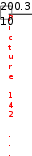X 20.0;

_Y 731

10

73,1

73,0 _;

3. 
   Найти отклонение показателей рядов «Х» и «Y» от своих средних арифметических величин (x_i- _X) и (y_i-_Y). Например: для уровня ФР₁₇₀ в
   

24.8 кГм/мин/кг отклонения от среднего значения будут равны: 24,8- 20,0= +4,8; для спортивного результата в 63 мин: 63-73= - 10 и т.д.;

4. 
   Вычислить квадраты найденных отклонений (x_i - _X )² и (y_i - _Y )²; получим: +4,8² =23,04; -10² =100 и т.д.;
   
5. 
   Найти суммы квадратов отклонений:
   

^{∑( xi -} X^{)2 = 95,87 ≈ 96; ∑( yi -}Y^{)2 = 459;}

6. 
   ^{Определить произведения отклонений (xi -} X^{) · (yi -}Y^); получим: (+4,8) · (-10) = -48 и т.д.;
   
7. 
   Найти сумму произведений отклонений:
   

^{∑(xi -} X^{) · (yi -} Y^{) = 174,91 ≈ 175;}

8. 
   Подставить найденное значение в формулу:
   

^rxy

175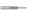

0,8 _;

94659

9. 
   Определить достоверность вычисленного коэффициента корреляции.
   

Если парных факторов меньше 100, то оценку достоверности целесообразно проводить по таблице критических значений коэффициента корреляции r (Приложение Д). Коэффициент корреляции r признается статистически значимым с вероятностью ошибки меньше 5 %, если его величина будет превышать табличное значение для соответствующего количества парных наблюдений в колонке α-0,05, (т.е. Р < 0,05), и с вероятностью ошибки меньше 1%, если его величина будет превышать табличное значение для соответствующего количества парных наблюдений в колонке α - 0,01, (т.е. Р < 0,01). В приведенном примере для 10 парных факторов табличные значения r составляют: при уровне значимости α 0,05 - 0,623, при α 0,01 - 0,765. Высчитанный коэффициент r расчетное равен 0,837, т.е. он больше табличного значения уровня значимости α 0,01. Т.е. его достоверность доказана с вероятностью ошибки Р < 0.01.

Если парных факторов больше 100, оценку достоверности коэффициента рекомендуется рассчитывать по формуле средней ошибки коэффициента корреляции 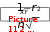(m_r):

m_r

Принято считать, что достоверным коэффициент корреляции может быть признан тогда, когда он превышает свою ошибку в три и более раз. В данном примере: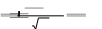

10.8²37

m_r 0.0