Методы_контроля_Командик (1). Ббк75. 1 я73 м 54 Рекомендовано к изданию Ученым советом Инновационного Евразийского университета Протокол 9 от
 Скачать 4.61 Mb. Скачать 4.61 Mb.
|
Проверка статистических гипотез с помощью непараметрических критериевВ педагогических исследованиях нередко возникает потребность рассчитать достоверность различий между небольшими совокупностями показателей, полученных по шкале наименований или шкале порядка, которые имеют порядковый, а не количественный характер выражения (например, места, занятые спортсменами на соревнованиях), В таких случаях прибегают к использованию непараметрическихкритериевразличия. Непараметрические критерии в отличие от параметрических имеют простую конструкцию, не требуют большой вычислительной работы, могут оценивать вариационные ряды порядкового характера любой формы распределения. Кроме того, они позволяют оценить сравнительно небольшие выборки, что важно для педагогических исследований. Существует несколько непараметрических критериев, которые, в зависимости от конструкции и статистической мощности, специфичны в решении тех или иных задач исследования. Рассмотрим один из них. Определение достоверности различий по критерию χ2Критерий χ2 (хи-квадрат) применяется для сравнения распределений испытуемых двух групп по состоянию некоторого свойства на основе измерений по шкале наименований. Для расчета достоверности различий результаты, полученные в обеих группах, распределяются в четырехпольные или многопольные таблицы в зависимости от того, на сколько классов (категорий) эти результаты подразделяются. Случай четырехпольной «таблицы»Допустим, проверяется эффективность использования специальной методики обучения подъему разгибом на перекладине. Для этой цели отобрано две равноценные группы по 25 человек в каждой: экспериментальная, в которой обучение ведется по экспериментальной методике, и контрольная, в которой обучение проводится по общеприня- той, традиционной, методике. Результаты обучения измеряются по шкале наименований, имеющей только две взаимоисключающие категории: выполнил – не выполнил. На основе таких измерений результатов обучения занимающихся в экспериментальной и контрольной группах составляется четырехпольная «таблица» 2x2 (данные заносятся в 4 поля - Э1, Э2, К1, К2). Таблица 22 – Четырехпольная таблица для расчета критерий χ2
В этой «таблице» Э1 – число занимающихся в экспериментальной группе, попавших в первую категорию (класс), например в категорию выполнивших подъем разгибом; Э2 – число занимающихся в экспериментальной группе, попавших во вторую категорию, например в категорию не выполнивших подъем разгибом; соответственно: К1 и К2 – то же самое в контрольной группе; N – общее число наблюдаемых (испытуемых), равное Э1 + Э2 + К1 + К2, или nэ+ nк. На основе данных такой «таблицы» можно проверить гипотезу о равенстве вероятностей попадания занимающихся экспериментальной и контрольной групп в первую (вторую) категорию. Такой гипотезой может быть, например, гипотеза о равенстве вероятностей выполнения подъема разгибом за- нимающимися в экспериментальной и контрольной группах. На этой основе можно судить об эффективности той или иной методики обучения. Для проверки гипотезы рассчитывается значение χ2 (хи- квадрат) по следующей формуле: 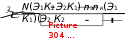 Полученное значение χ2расчетн сравнивается с критическим значением χ2крит при числе степеней свободы V= С – 1 и уровне значимости 0,05,  расчетн где С – число категорий. Если полученное значение хи-квадрат (χ2 ) больше критического (χ2крит), т.е. χ2расчетн > χ2крит, то считается, что распределение полученных результатов в ту или иную категорию не случайное и, следовательно, одна из применяемых методик обучения более эффективна, и наоборот, когда χ2расчетн < χ2крит, распределение полученных результатов в ту или иную категорию считается случайным, и в данном случае нет оснований говорить о преимуществах какой-либо из применявшихся методик. Критерий не рекомендуется использовать, если N = nэ+ nк < 20, и в случае, когда хотя бы одна из абсолютных частот (Э1, Э2, К1, К2) в таблице 2x2, составленной на основе экспериментальных данных, меньше 5, (т.е. если в какую-то категорию одной из групп попало меньше 5 человек). В случае же если хотя бы одна из абсолютных частот имеет значение, заключенное в пределах от 5 до 10, применение критерия возможно при внесении некоторых изменений в формулу. Тогда значение χ2 подсчитывается по следующей формуле: 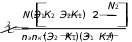 Для наглядности проставим конкретные значения в четырехпольную «таблицу» с учетом нашего примера и выявим достоверность различий между полученными результатами. Например, из 25 занимающихся в экспериментальной группе после обучения подъему разгибом выполнили 20 чел. не смогли выполнить 5 чел. В контрольной – 13 и 12 соответственно. Составим на основании этих результатов четырехпольную таблицу: Таблица 23 – Исходные данные для расчета критерий χ2 с помощью четырехпольной таблицы
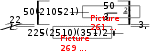 Из таблицы 23 видно, что все значения абсолютных частот не меньше 5, но одно значение Э2 равно 5, поэтому расчет необходимо произвести по второй формуле Теперь необходимо это значение, т.е χ2расчетн, сравнить с χ2крит, для чего вначале определяем число степеней свободы V=С-1=2-1=1 (Напомним, что С – число категорий, в нашем примере их две – «выполнил», «не выполнил»). Дальше из таблицы (приложение В) находим значение χ2крит, которое равно 3,8. Отсюда верно неравенство χ2расчетн < χ2крит (3,2 < 3,8), следовательно, большее количество занимающихся в экспериментальной группе, сумевших в данном случае выполнить подъем разгибом, имеет случайный характер (Р>0,05, т.е. вероятность ошибки больше 5 %), и, видимо, зависит от других факторов, не связанных с методикой обучения. Поэтому говорить о том, что экспериментальная методика была более эффективной, нет оснований. |
