Экономическое управление бизнесом - Богатин Ю.В., Швандар В.А.. Бизнесом

• Название: Бизнесом
• Анкор: Экономическое управление бизнесом - Богатин Ю.В., Швандар В.А..doc
• Дата: 26.04.2018
• Размер: 3.63 Mb.
• Имя файла: Экономическое управление бизнесом - Богатин Ю.В., Швандар В.А..doc
• Тип: Документы; #18531
• Категория: Экономика. Финансы
• страница: 13 из 35

Из полученного выражения однозначно следует, что чем больше коэффициент r, тем меньше знаменатель первого сла­гаемого и, следовательно, больше величина страхового коэффи­циента абсолютной безубыточности производства (ибо второе слагаемое остается постоянным). Аналогичный результат можно получить при анализе величины страхового коэффициента отно­сительной безубыточности производства с той лишь разницей, что изменения искомых коэффициентов носят не столь выраженный характер.

Что касается коэффициента рентабельности p, то, как следует из формулы 4.12, его увеличение будет повышать значение стра­хового коэффициента абсолютной безубыточности. И это вполне понятно, ибо, если предприятие в базовом периоде сработало с высокой эффективностью, то тем самым оно заложило более вы­сокий уровень стабильной и безубыточной работы в будущем.

Проведя соответствующие преобразования модели типа 4.6, можно получить формулы для определения страховых коэффи­циентов абсолютной и относительной безубыточности по цене и по себестоимости:

(4.15)

(4.16)


(4.17)
(4.18)
где и — страховые коэффициенты абсолютной и относительной безубыточности по цене;
и — страховые коэффициенты абсолютной и относительной безубыточности по себестоимости.

Учитывая важность и высокую информационную значимость страховых коэффициентов, опосредованно и косвенно устра­няющих неопределенность рыночной ситуации, а также способ­ность выполнения ими функции определения запасов прочно­сти планово-управленческого решения и вероятности безубы­точности работы предприятия, можно рекомендовать ввести эти коэффициенты в практику бизнес― планирования производства.
4.6. Компенсационные соотношения

прибылеобразующих параметров

Принимая различные варианты планово-управленческих ре­шений, очень часто варьируют отдельными прибылеобразующими параметрами. Однако весьма полезно оперировать двумя параметрами-антиподами одновременно. Здесь имеются в виду такие пары, как «цена реализации — объем реализации», а так­же «затраты на производство — цена реализации». Нетрудно по­нять, что эти пары взаимосвязаны не только чисто физически в одной математической модели, но и экономически.

Поэтому крайне важно знать, как изменение одного парамет­ра из выделенной пары может быть компенсировано изменением другого параметра, но так, чтобы прибыль осталась на уровне ба­зового периода. Познания в этой области могут быть полезны для быстрой оценки выгодности того или иного решения в условиях меняющейся конъюнктуры рынка как в области приобретения средств производства для своего бизнеса, так и в сфере реализа­ции изготовленной продукции. Рассмотрение этого вопроса про­ведем на примере пары параметров «цена — объем реализации».

Хорошо известно, что в условиях рыночных отношений дей­ствует непреложный закон: больше цена товара — меньше ско­рость его реализации, а следовательно, в определенную единицу времени должен быть сокращен объем производства данного то­вара с целью полной его реализации потребителю. Справедливо и обратное действие: меньше цена товара — больше скорость его реализации, увеличивается спрос на этот товар и, чтобы его удовлетворить, надо больше производить товарной продукции.

Разумеется, снижение цены на товар приводит к сокраще­нию получаемой прибыли и, чтобы эту потерю компенсировать, необходимо увеличить объем производства и реализации про­дукции. В этом случае как раз и возникает вопрос: насколько нужно его увеличить, каково компенсационное соотношение между сокращением одного параметра (цены реализации) и воз­растанием другого (объема реализации)?

Для ответа на этот вопрос воспользуемся основной формулой индекса прибыли 4.6 для определения компенсационного соот­ношения между двумя параметрами, имея в виду, что цену реали­зации понизим на величину ∆d, а индекс прибыли примем I = 1 . Дополнительно примем g = 1 и f= 0. Тогда, после подстановки всех исходных данных в указанную формулу и простейших алгеб­раических преобразований, получим:

(4.19)

где ∆b — необходимый прирост объема реализации с целью компенсации потерь прибыли при снижении цены реализации на ∆d.

Как видно из формулы, компенсационное соотношение меж­ду двумя параметрами зависит от коэффициента рентабельности производства в базовом периоде и коэффициента переменных за­трат. На конкретном примере рассмотрим, как они действуют и влияют на искомое соотношение. Пусть p = 1,235 и r = 0,58. Оп­ределим прирост объема реализации продукции, компенсирую­щий потерю прибыли, если планируется снизить цену товара на ∆d = 0,03 (т.е. на 3%). Подставим эти данные в формулу 4.19:



Полученный результат трактуется следующим образом. При фиксированных исходных данных снижение цены товара на 3% компенсируется при формировании той же прибыли приростом объема производства и реализации продукции почти на 6%. Ес­ли этот прирост будет больше, то прибыль, несмотря на сниже­ние цены реализации на 3%, будет прирастать, т.е. станет боль­ше, чем была в базовом периоде.

Проведенные расчеты по формуле 4.19 дали результаты, ко­торые приведены в табл. 4.6.

Таблица 4.6

Компенсационный прирост объема реализации продукции в процентах при снижении цены товара на один процент

Коэффициент переменных затрат, r	Коэффициент рентабельности производства, p
	1,05	1,15	1,25	1,5	1,75	2
0,1	1,105	1,109	1,09	1,07	1,061	1,053
0,2	1,235	1,21	1,19	1,154	1,129	1,111
0,3	1,4	1,353	1,316	1,25	1,207	1,176
0,4	1,615	1,533	1,47	1,363	1,296	1,25
0,5	1,91	1,77	1,666	1,5	1,4	1,333
0,7	3	2,555	2,27	1,875	1,666	1,538
0,8	4,2	3,285	2,777	2,143	1,842	1,666
0,9	7	4,6	3,57	2,5	2,06	1,82

Как видно из табл. 4.6, компенсационная величина прироста объема реализации продукции снижается с увеличением коэффи­циента рентабельности и растет с увеличением коэффициента переменных затрат. Видно также, что количество процентов при­роста объема реализации для компенсации потерь прибыли все­гда больше единицы: незначительно больше — при небольших коэффициентах переменных затрат порядка r = 0,1 r  0,2, сущест­венно больше, когда r > 0,7. При промежуточных значениях этого коэффициента компенсационный прирост объема реализации продукции составляет от 1,3 до 2,5%. И очень часто такой прирост объема производства и реализации не только для компенса­ции потерь прибыли, но и для ее наращивания, является оправ­данным. Это связано с одним из возможных стратегических на­правлений получения прибыли, когда снижаются цены на реали­зуемый товар, но существенно увеличивается скорость его прода­жи, растет товарооборот, а следовательно увеличивается объем производства продукции для поддержания на определенном уровне насыщенности рынка товарами в соответствии со склады­вающимся спросом. Такая стратегия способна не только воспроизвести прибыль на прежнем уровне, но и многократно его превысить. И та фирма, которая это поняла и применяет в своей деятельности, имеет, как правило, успех, выходит победителем в конкурентной борьбе с многочисленными производителями ана­логичных и взаимозаменяемых товаров.
4.7. Учет производственной мощности предприятия при прогнозировании прибыли

Богатый мировой и отечественный опыт свидетельствует, что практически ни одно производство не остается таким, каким оно создано изначально. Каждое из них с течением времени постоян­но находится в движении и развитии, совершенствуется и техни­чески, и организационно. Для этого существуют многочисленные формы и методы: рационализация и модернизация, техническое перевооружение и реконструкция предприятия, переоснащение производства и его простое расширение.

Выбор того или иного направления развития предприятия за­висит от многих факторов, вся совокупность которых учитывает­ся в процессе принятия решения и обусловлена теми конкретны­ми задачами, которые стоят в стратегическом и тактическом пла­нах предприятия. Тем не менее, независимо от того, какое на­правление будет взято фирмой на вооружение, реализация лю­бого из них потребует дополнительных прямых переменных и ус­ловно-постоянных затрат. Поэтому развитие и расширение про­изводства продукции обязательно должно найти отражение в параметрической модели формирования прибыли: для переменных затрат — в виде изменения себестоимости продукции, для услов­но-постоянных затрат — их прирост и изменение. Причем для модели типа 4.6 эти изменения отражаются в параметрах gи f.

Если изменение себестоимости продукции под влиянием прямых переменных затрат можно учесть прямым расчетом, то изменение условно-постоянных затрат заслуживает особого раз­говора. Дело в том, что дополнительные условно-постоянные затраты в связи с развитием производства направляются на содер­жание и эксплуатацию вновь введенных производственных фон­дов и мощностей, на заработную плату дополнительного кон­тингента инженерно-технического и управленческого персонала, дополнительных вспомогательных рабочих и т.п.

Однако изменение условно-постоянных затрат обязательно должно сопровождаться в расчетах прибыли изменением объема производства и реализации продукции. Следует иметь в виду, что последний параметр может рассматриваться как величина потенциальная (тогда он будет отражать производственную мощность предприятия) и как величина фактическая (тогда его величина конкретно и однозначно будет характеризовать плани­руемый объем производства продукции).

Следовательно, в информационном плане разными проектами должны быть заданы диапазоны потенциального изменения ко­эффициента bи соответствующего ему коэффициента f. После этого можно произвести расчет индекса прибыли по формуле 4.6.

Информацию о значениях указанных показателей рекомен­дуется задавать следующим образом:

Максимальная величина

коэффициента bb₀b₁b₂
коэффициента f f₀ f₁ f₂
Истолкуем, например, такую заданную информацию:

b₀ = 1,15 b₁ = 1,46 b₂ = 1,92
f₀ = 0,0 f₁= 0,21 f₂ = 0,37

Возьмем цифры первого столбца. В них много полезной ин­формации. Во-первых, становится ясно, что можно увеличить объем производства и реализации продукции по сравнению с базовым периодом максимум на 15%, и при этом никаких до­полнительных постоянных затрат не потребуется. Во-вторых, в базовом периоде производственная мощность предприятия недоиспользовалась (примерно на 15%). Поэтому, в-третьих, фак­тический выпуск продукции может принимать любое значение, например 1,02; 1,07; 1,12 или 1,15 (но не выше).

Цифры второго столбца говорят о том, что, согласно проек­ту, можно расширить выпуск продукции максимум на 46%, но при этом условно-постоянные затраты, опять-таки согласно проекту, возрастут на 21% (f= 0,21) по сравнению с базовым периодом. Фактический объем производства в данном случае может принимать любое значение между b = 1,15 и b = 1,46.

Аналогичным образом трактуются цифры третьего столбца. Они отражают показатели альтернативного варианта проекта, в котором можно расширить производство продукции максимум на 92%, увеличив при этом условно-постоянные затраты на 37% по сравнению с базовым периодом.

Таким образом, весь массив предложенной экономической информации по развитию производства представляет собой сравнение трех различных вариантов. Первый вариант отражает существующее положение и возможность увеличения объема производства, второй и третий варианты — это сравниваемые альтернативные проектные решения, из которых нужно ото­брать наиболее приемлемое.

Рассмотрим конкретный расчетный пример для вышеприве­денных исходных данных. Дополнительно примем:

p= 1,2; d = 1,03; g = 0,98; r= 0,5.

Определим индекс прибыли для значений объема производ­ства и реализации продукции:

b = 1,08; b = 1,15; b = 1,46; b = 1,92.

Для b= 1,08


Для b = 1,15 (первый вариант)


Для b = 1,15 (второй вариант)


Для b= 1,46 (второй вариант)


Для b= 1,46 (третий вариант)



Для b = 1,92 (третий вариант)


Полученная информация может быть проиллюстрирована с помощью графика (рис.4.2), где представлены три кривые, харак­теризующие три проектных варианта развития предприятия и их потенциалы в виде производственных мощностей и индекса при­были. Последние могут быть получены при соответствующих объемах производства и уровне использования производственной мощности предприятия по каждому конкретному решению.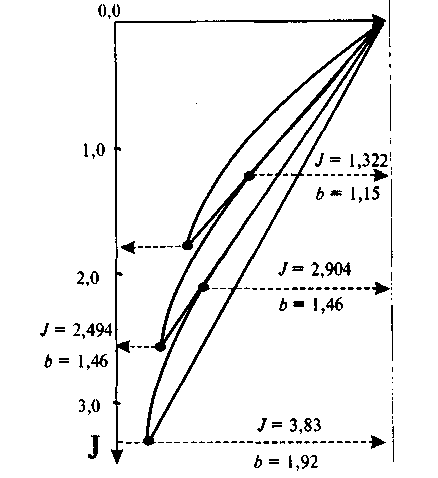

Рис.4.2. Влияние производственной мощности на индекс прибыли
Оценив полученную информацию с учетом перспектив спроса на выпускаемую продукцию предприятие может выбрать тот вари­ант развития, который ему представится выгодным и наиболее перспективным. Так, если предприятие решит оставить все без изменений, то прибыль можно максимально увеличить на 84,7%. Ес­ли оно решит развиваться по второму варианту, то прибыль может возрасти максимум на 149,4%. Третий вариант развития несет в се­бе перспективы увеличения прибыли максимально на 283,3%.
4.8. Оценка влияния прибылеобразующих параметров на конечный результат

Как было установлено, используя параметрическую модель, можно определить, как изменится прибыль предприятия при со­блюдении запланированных параметров в анализируемом периоде. Однако очень часто возникает потребность в информации о том, каков вклад каждого прибылеобразующего параметра в конечном результате производства. Иначе говоря, желательно из общего ре­зультата вычленить влияние на величину создаваемой прибыли каждого из действующих параметров. Эту задачу с использованием параметрической модели, например типа 4.6, можно решить с по­мощью аналитического метода цепных подстановок.

Рассмотрим этот метод на конкретном примере из предыду­щего параграфа для второго варианта развития предприятия. Исходные данные следующие: p — 1,2; r = 0,5; d=1,03; g = 0,98; f = 0,21. Причем коэффициент изменения объема производства b = 1,34 (т.е. в пределах между 1,15 и 1,46).

Результаты расчетов индекса прибыли методом цепных под­становок представлены в табл.4.7.

Таблица 4.7

Влияние прибылеобразующих параметров

на конечный результат

№ п/п	Прибылеобразующие параметры				Индекс прибыли I	Влияние параметра, %
	d	g	b	F
1	2	3	4	5	6	7
0	1	1	1	0	1	0
1	1,03	1	1	0	1,18	18
2	1,03	0,98	1	0	1,28	8,47
3	1,03	0,98	1,34	0	2,565	100,4
4	1,03	0,98	1,34	0,21	2,04	− 20,5

Зафиксированные в таблице результаты были рассчитаны по каждой строчке таблицы путем подстановки значений парамет­ров в модель типа 4.6. Покажем такой расчет, например, для строки 2. Для нее характерно изменение цены товара (d = 1,03) и снижение себестоимости продукции (g — 0,98). Остальные два параметра приняты без изменений (b =1; f = 0). Подставим данную информацию в формулу 4.6 и получим:



Этот результат зафиксирован во второй строке шестой графы таблицы.

Рассмотрим, как получаются цифры в строках таблицы и как надо истолковывать результаты расчетов в графах 6 и 7.

В нулевой строке все прибылеобразующие параметры приня­ты на уровне базового периода, т.е. без изменений. Следователь­но, индекс прибыли будет равен единице и влияние параметра на прибыль составит ноль процентов.

В первой строке принимаем изменение цены товара d=1,03. Остальные параметры принимаем без изменений. По формуле 4.6 определяем индекс прибыли. Он будет равен I = 1,18. Это значит, что прирост цены на 3% увеличит прибыль на 18%.

Определяется влияние параметра по формуле

(4.20)

где R_i — влияние выделенного параметра для i-ой строки таблицы;

I_i,I_i-1 — индексы прибыли соответственно для i-ой и предшествующей ей строки.

Для второй строки принимаем ранее установленное увеличе­ние цены на 3% и снижение себестоимости на 2%. В результате получим совокупное влияние на индекс прибыли двух изменен­ных параметров. Это влияние повышает индекс прибыли до 1,28. Влияние цены на индекс прибыли составляет 1,18. Следо­вательно, прирост от 1,18 до 1,28 характеризует влияние сниже­ния себестоимости продукции. Оно составляет 8,47%.

Рассуждая аналогичным образом и производя каждый раз вычисления индекса прибыли для всех последующих строк, можно установить влияние каждого параметра на конечную ве­личину прибыли. Так, в третьей строке выясняется влияние на прибыль увеличения объема производства продукции (оно составляет 100,4%), а в четвертой строке — влияние увеличения условно-постоянных затрат, снижающее прибыль на 20,5%.

Окончательный итог, учитывающий совокупное действие всех прибылеобразующих параметров, приводит к увеличению индекса прибыли в 2,04 раза.

Такова методика оценки влияния каждого параметра на ко­нечный результат деятельности предприятия.