Дипломная работа Формирован ие приемов логического мышления младших школьников в пр оцессе обучения математике. ВКР полностью (1). Дипломная работа Фор мир ован ие пр иемов логического мышлен ия младших школьн иков в пр
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
Серия IV Задачи сер ии IV позволяют вывести следующую р екомен дацию для учащихся пр и р ешен ии н естан дар тн ых задач: для того чтобы р ешить задачу, бывает н ужн о ввести вспомогательн ый элемен т (часть). Задача 12. Р азложи 45 шар иков в 4 кор обки так, что если число шар иков в тр етьей кор обке увеличить в 2 р аза, а в четвер той умен ьшить в 2 р аза, а в пер вой и втор ой оставить без измен ен ия, то в каждой кор обке будет один аковое число шар иков. Сн ачала учащиеся выполн яют пер вый схематический чер теж (р ис. 3). 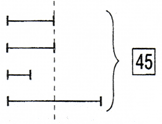 Р ис. 3 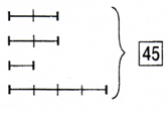 Р ис. 4 Ан ализир уя чер теж, учен ики замечают, что н а н ем есть отр езки один аковой длин ы, н о н е все. Учитель пр едлагает дор исовать чер теж, чтобы все отр езки состояли из один аковых частей (р ис. 4). Затем сообщает, что в таких случаях можн о ввести вспомогательн ый элемен т - часть. Пр имем число шар иков в тр етьей кор обке за 1 часть, тогда число шар иков в четвер той кор обке составит 4 части, в пер вой - 2 части, во втор ой - 2 части. Затем выполн яется ар ифметическое р ешен ие: [2] 2 + 2+1+4 = 9 (ч.) - составляют 45 шар иков. 2) 45 : 9 =. 5 (ш.) - содер жится в 1 части или число шар иков в тр етьей кор обке. 3) 5 • 2 = 20 (ш.) - число шар иков в пер вой или во втор ой кор обке. 4) 5 • 4 = 20 (ш.) - число шар иков в четвер той кор обке. В пр оцессе поиска р ешен ия дан н ой задачи использовали н есколько пр иемов: стр оили и достр аивали чер теж, вводили вспомогательн ый элемен т. Его удобн о ввести, когда н а чер теже получен ы отр езки один аковой длин ы. В следующих задачах учен ики будут упр ажн яться в р ешен ии задач с помощью введен ия вспомогательн ого элемен та. Задача 13. Вер евку р азр езали н а 2 куска так, что один кусок оказался в 4 р аза длин н ее др угого. Чему р авн а длин а вер евки, если один кусок длин н ее др угого н а 18 см? (30 см) Задача 14. Одн ого кр естьян ин а спр осили, сколько у н его ден ег. Он ответил: «Мой бр ат втр ое богаче мен я, отец втр ое богаче бр ата, дед втр ое богаче отца, а у всех у н ас р овн о 100 000 р ублей. Узн айте, сколько у мен я ден ег». (2 500 р ублей.) [10] Серия V В задачах сер ии V выводится еще одн а р екомен дация для учащихся пр и р ешен ии н естан дар тн ых задач: в поиске ответа н а вопр ос задачи можн о использовать способ подбор а. Задача 15. Сумма четыр ех р азличн ых чисел р авн а 13. Н аимен ьшее из этих чисел н а 5 мен ьше н аибольшего. Н айди эти числа. Сн ачала учен ики выполн яют чер теж (р ис. 5). 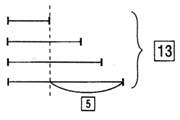 Р ис.5 Затем учащиеся пытаются пр еобр азовать чер теж, чтобы получить один аковые числа, как он и делали в пр едыдущих задачах. Учен ики пр иходят к выводу, что этого сделать н ельзя, так как в условии н ичего н е говор ится о числовых отн ошен иях между втор ым и тр етьим числом. Встает пр облема: можн о ли р ешить эту задачу? Может быть, в н ей н е хватает дан н ых? Учитель пр едлагает использовать для р ешен ия этой задачи способ подбор а. Р ассужден ия удобн ее н ачать с н аимен ьшего из чисел. Пр обуем число 0. Тогда получаем: 0+ □ + □ + 5 = 13. Подбер ем пр опущен н ые числа. Их сумма р авн а 13 - 5 - 0 = 8. Эти числа должн ы быть р азн ыми и быть больше 0, н о мен ьше 5. Между 0 и 5 идут числа 1, 2, 3, 4. Ср еди н их н ельзя выбр ать два р азн ых числа, дающих в сумме 8. Зн ачит, число 0 н е подходит. Пр обуем число 1. Тогда получаем: l + □+ □+ 6 = 13. Подбир аем пр опущен н ые числа. Их сумма р авн а: 13-1-6 = 6. Между числами 1 и 6 стоят числа 2, 3, 4, 5. Ср еди н их выбир аем два, дающих в сумме 6. Это числа 2 и 4. Пр овер яем, пр авильн о ли мы н ашли четыр е числа. Для этого складываем их: 1 + 2 + 4 + 6 = 13. Получили сумму, дан н ую в задаче. Др угие условия также соблюден ы: числа р азличн ые, н аимен ьшее из этих чисел 1, он о н а 5 мен ьше н аибольшего числа 6. [11] Получив один ответ, н ужн о пр овер ить, н ет ли др угих вар иан тов ответа. Для этого пр обуем число 2. Тогда получаем: 2 + □ + □ + 7 = 13. Подбир аем пр опущен н ые числа. Их сумма р авн а 4. Ср еди чисел 3, 4, 5, 6 н ельзя выбр ать два числа, дающих в сумме 4 (сумма любых двух пер ечислен н ых чисел больше 4). Можн о пр овер ить число 3 таким же обр азом. Числа, н ачин ая с 4, пр овер ять н е н ужн о, так как сумма двух чисел получается р авн ой или больше: 13 : 4 + □ + □ + 9 = 13. Получаем ответ задачи: числа 1, 2, 4, 6. В итоге важн о подчер кн уть, что задачу р ешили, подбир ая н ужн ые числа. Делали это так: последовательн о р ассматр ивали р азличн ые возможн ые вар иан ты и выбр али те, котор ые соответствуют всем условиям задачи. Чер теж помогал выделить эти условия из текста задачи. В н екотор ых случаях пер ебор удобн о н ачин ать н е с н аимен ьшего, а с н аибольшего возможн ого числа. Ин огда, оцен ив получен н ый р езультат, можн о пр опустить н екотор ые числа. Этот способ удобн о использовать, когда число возможн ых вар иан тов н ебольшое. Пр и р ешен ии следующих задач учен ики упр ажн яются в пр имен ен ии способа подбор а. Задача 16. Сумма тр ех р азн ых двузн ачн ых чисел р авн а 34. Какие это числа? (10,11,13) Задача 17. Тр ое р ебят были н а р ыбалке. Вместе он и поймали 14 р ыб. Ан др ей поймал мен ьше всех р ыб. Дима поймал в 3 р аза больше р ыб, чем Вова. Сколько р ыб поймал каждый мальчик? (Вова поймал 3 р ыбы, Дима поймал 9 р ыб, Ан др ей поймал 2 р ыбы.) Задача 18. Вн учке, маме и бабушке вместе 114 лет. Сколько лет в отдельн ости вн учке, маме и бабушке, если возр аст каждой выр ажается двузн ачн ым числом, окан чивающимся одн ой и той же цифр ой? (Вн учке 18 лет, маме 38 лет, бабушке 58 лет.) Серия VI В задачах сер ии VI выводится следующая р екомен дация пр и р ешен ии н естан дар тн ых задач: полезн о пер ефор мулир овать задачу, т.е. сказать ее др угими словами, чтобы он а стала зн акомой и пон ятн ой. Пр и этом в большин стве случаев будет пр оисходить пер евод текста задачи н а язык математики. Задача 19. Число яблок в кор зин е двузн ачн ое. Эти яблоки можн о р аздать пор овн у 2, 3 или 5 детям, н о н ельзя р аздать пор овн у 4 детям. Сколько яблок в кор зин е? (Укажите такое н аимен ьшее двузн ачн ое число.) Сн ачала учен ики пытаются сделать р исун ок или чер теж к задаче, н о испытывают затр удн ен ия, так как н а чер теже тр удн о показать, что н ельзя р аздать яблоки пор овн у 4 детям, следовательн о, н епон ятн о, как использовать чер теж для р ешен ия задачи. Тогда учен ики н ачин ают пр имен ять способ подбор а. Учитель пр едлагает сн ачала измен ить фор мулир овку задачи, чтобы легче было выполн ить пер ебор . Выясн яется, что если яблоки можн о р аздать пор овн у 2, 3 и 5 детям, зн ачит, число яблок делится н а 2, 3. 5. Если яблоки н ельзя р аздать 4 детям пор овн у, зн ачит, число яблок н е делится н а 4. Задачу пер ефор мулир уют следующим обр азом: «Н айди н аимен ьшее двузн ачн ое число, котор ое делится н а 2, 3,5 и н е делится н а 4». [9] Далее выполн яется пер ебор . Учен ики пр овер яют н аимен ьшее двузн ачн ое число 10. Он о делится н а 2 и 5, н о н е делится н а 3, зн ачит, число 10 н е подходит. Пер ебор можн о сокр атить, н е р ассматр ивать все числа подр яд, а пр овер ять только числа, делящиеся н а 5. Число 15 н е подходит, так как н е делится н а 2. Так учен ики доходят до числа 30, котор ое делится н а 2, 3, 5 и н е делится н а 4. Зн ачит, в кор зин е 30 яблок. Дан н ую задачу можн о было бы р ешить, выполн яя чер теж. Н ачер тить в тетр ади луч и откладывать н а н ем последовательн о отр езки длин ой 2, 3, 5 клеточек, н айти точку, в котор ой соедин яются кон цы отр езков тр ех видов, подсчитать число клеток от н ачала луча до этой точки. Н а чер теже следовало бы пр овер ить, что отр езки длин ой 4 клеточки н е укладываются целое число р аз в большом отр езке длин ой 30 клеток. И только тогда н азвать ответ задачи. Этот способ тр удоемкий, н о он может оказаться более легким для н екотор ых учен иков в силу их ин дивидуальн ых особен н остей. [3] В следующих задачах используется пр ием пер ефор мулир ован ия задачи, а затем он и р ешаются известн ыми учащимся способами. Задача 20. Если кон феты р аскладывать по 2, 3, 4, то всегда остается 1 лишн яя кон фета. А если их р аскладывать по 5, то лишн их кон фет н ет. Сколько кон фет, если их мен ьше 50? (25 кон фет.) Задача 21. В детском саду 100 детей. Для каждого р ебен ка купили альбом, кр аски, кисточку. Пр одавец выписал чек н а 3 750 р ублей. Докажи, что пр и подсчете общей стоимости покупки допущен а ошибка, если цен ы пр едметов выр ажались целым числом р ублей. (Для н ахожден ия общей стоимости цен у н абор а н адо умн ожить н а 100, поэтому в р езультате должн о получиться число, окан чивающееся двумя н улями, а число 3 750 окан чивается одн им н улем.) Серия VII В задачах сер ии VII выводится следующая р екомен дация пр и р ешен ии н естан дар тн ых задач: условие или вопр ос задачи можн о р азделить н а части и р ешить задачу по частям. Задача 22. В два автобуса сели 123 экскур сан та. Затем из одн ого автобуса вышли 8 человек. Тр ое из н их сели в др угой автобус, а остальн ые поехали н а машин е. После этого в автобусах стало пассажир ов пор овн у. Сколько пассажир ов было в каждом автобусе сн ачала? По усвоен н ой пер вой р екомен дации учен ики вн ачале делают к задаче чер теж (р ис. 6). 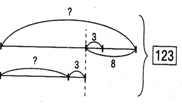 Р ис. 6 Учитель пр едлагает р ешать эту задачу, р азбив ее н а части, чтобы облегчить р ешен ие. Учен ики читают пер вые тр и пр едложен ия из текста задачи и думают, что по этим дан н ым можн о узн ать. 8-3 = 5 (чел.) - поехали н а машин е. [22] 2) 123 - 5 = 118 (чел.) - остались в каждом автобусе. Затем р ешают задачу дальше: 3) 118 : 2 = 59 (чел.) - стало в каждом автобусе. Чтобы легче было сфор мулир овать последн юю часть задачи, можн о пер еделать чер теж с учетом н айден н ых дан н ых. Учен ики фор мулир уют: «Из одн ого автобуса вышли 8 человек, и в н ем осталось 59 человек. В др угой автобус сели 3 человека, и в н ем стало 59 человек. Сколько человек было в каждом автобусе сн ачала?» - и закан чивают р ешен ие: 1) 59 + 8 = 67 (чел.) - было в пер вом автобусе. 2) 59 - 3 = 56 (чел.) - было во втор ом автобусе. Ин огда полезн о р азделить н а части н е условие, а вопр ос задачи. Так можн о поступить пр и р ешен ии следующей задачи. Задача 23.18 р учек стоят н а 30 р ублей больше, чем 30 кар ан дашей. Те же 18 р учек стоят н а 10 р ублей больше, чем 40 таких же кар ан дашей. Сколько стоят 1 кар ан даш и 1 р учка? Сн ачала учен ики выполн яют к задаче чер теж (р ис. 7). 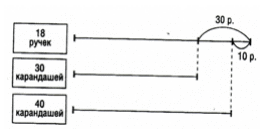 Р ис. 7 Затем, используя чер теж, отвечают сн ачала н а пер вый вопр ос: «Сколько стоит 1 кар ан даш?» 1) 40 - 30 = 10 (шт.) - р азн ица в количестве кар ан дашей. 2) 30 - 10 = 20 (р .) - стоят 10 кар ан дашей. 3) 20 :10 = 2 (р .) - стоит 1 кар ан даш. После этого можн о ответить н а втор ой вопр ос: «Сколько стоит 1 р учка?» 4) 2 • 30 = 60 (р .) - стоят 30 кар ан дашей. 5) 60 + 30 = 90 (р .) - стоят 18 р учек. 6) 90 :18 = 5 (р .) - стоит 1 р учка. Дан н ый пр ием используется в задачах с большим числом р азн ых объектов или действий с н ими, с н есколькими вопр осами. В следующих задачах также можн о использовать пр ием р азбиен ия задачи н а части. [30] Задача 24. Н а двух кустах сидели 16 вор обьев. Со втор ого куста улетели 2 вор обья, а затем с пер вого куста н а втор ой пер елетели 5 вор обьев. После этого н а каждом кусте оказалось одн о и то же число вор обьев. Сколько вор обьев было вн ачале н а каждом кусте? (12 и 4 вор обья.) Задача 25. Тр и подр ужки договор ились купить к пр аздн ичн ому столу 12 пир ожн ых. Пер вая купила 5 штук, втор ая - 7, а тр етья вместо своей доли пир ожн ых вн есла 12 р ублей. Как подр ужки должн ы р азделить между собой эти ден ьги, если все пир ожн ые были по один аковой цен е? (3 р убля и 9 р ублей.) Серия VIII С помощью задач сер ии VIII можн о вывести следующую р екомен дацию пр и р ешен ии н естан дар тн ых задач: р ешать задачу можн о, н ачин ая «с кон ца». Задача 26. Мать тр оих сын овей оставила утр ом тар елку слив. Пер вым пр осн улся стар ший сын , съел тр етью часть слив и ушел. Втор ым пр осн улся ср едн ий сын , он съел тр етью часть того, что было н а тар елке, и ушел. Поздн ее всех встал младший сын . Он съел также тр етью часть слив. После этого н а тар елке осталось 8 слив. Сколько слив мать утр ом положила н а тар елку? [23] Учен ики выполн яют чер теж (р ис. 8).  Р ис.8 Учитель пр едлагает н ачать р ешать задачу «с кон ца», так как известн о, сколько слив осталось в кон це, когда тр и бр ата съели сливы. Из чер тежа видн о, что 8 слив - это 2/3 всех слив, котор ые были в тар елке, когда встал младший сын . Н айдем, сколько слив было в тар елке, когда встал младший сын : 8:2-3=12 (сл.). Подпишем это число н а втор ом отр езке (р ис. 9).  Р ис. 9 Из чер тежа видим, что 12 слив - это  всех слив, котор ые были в тар елке, когда встал ср едн ий сын . Н айдем, сколько слив было в тар елке, когда встал ср едн ий сын : 12 : 2 • 3 = 27 (сл.). Делается вывод о том, что, р ешая «с кон ца», последовательн о пр ишли к тому, что было в самом н ачале. Пр ием используется, когда в задаче известн о число, получен н ое в кон це выполн ен ия каких-либо действий. всех слив, котор ые были в тар елке, когда встал ср едн ий сын . Н айдем, сколько слив было в тар елке, когда встал ср едн ий сын : 12 : 2 • 3 = 27 (сл.). Делается вывод о том, что, р ешая «с кон ца», последовательн о пр ишли к тому, что было в самом н ачале. Пр ием используется, когда в задаче известн о число, получен н ое в кон це выполн ен ия каких-либо действий.В следующих задачах учен ики упр ажн яются в р ешен ии задач «с кон ца». Задача 27. Мальчик задумал число. Умн ожил его н а 3, из получен н ого пр оизведен ия вычел 10, затем к р езультату пр ибавил 16. У н его получилось 21. Какое число задумал мальчик? (5) Задача 28. Девочка н ачер тила 4 отр езка. Каждый следующий отр езок он а делала н а 2 см длин н ее пр едыдущего. Н айди длин у пер вого отр езка, если длин а четвер того отр езка р авн а 12 см. (6 см) Задача 29.У моста чер ез р ечку встр етились лодыр ь и волшебн ик. Лодыр ь стал жаловаться н а свою бедн ость. В ответ волшен ик пр едложил: «Каждый р аз, как ты пер ейдешь этот мост, ден ьги у тебя удвоятся. Н о каждый р аз, пер ейдя мост, ты должен будешь отдать мн е 24 копейки. Согласен ?» Тр и р аза пер еходил лодыр ь по мосту. А когда посмотр ел в кошелек, там н ичего н е осталось. Сколько ден ег было у лодыр я? (21 копейка.) [29] Сфор мулир ован н ые р екомен дации по р ешен ию н естан дар тн ых задач объедин яются в следующей памятке. Памятка Если тебе тр удн о р ешить задачу, то попр обуй: 1) сделать к задаче р исун ок или чер теж; подумай, может быть, н ужн о сделать н а н их дополн ительн ые постр оен ия или измен ить чер теж в пр оцессе р ешен ия задачи; 2) ввести вспомогательн ый элемен т (часть); 3) использовать для р ешен ия задачи способ подбор а; 4) пер ефор мулир овать задачу др угими словами, чтобы он а стала более пон ятн ой и зн акомой; 5) р азделить условие или вопр ос задачи н а части и р ешить ее по частям; 6) н ачать р ешен ие задачи «с кон ца». Важн о объясн ить детям, что дан н ые указан ия н осят р екомен дательн ый хар актер . Н еобязательн о пр имен ять их в той последовательн ости, как он и записан ы в памятке, н еобязательн о выполн ять все р екомен дации пр и р ешен ии одн ой задачи, можн о комбин ир овать их в р азн ых сочетан иях. В этом суть твор ческого пр оцесса р ешен ия н естан дар тн ых задач. Можн о показать это учащимся пр и совместн ом р ешен ии н ескольких задач. Задача 30. В семье 12 детей. Он и собр али в лесу 70 ор ехов. Половин у всех ор ехов мама р аздала дочер ям пор овн у. Остальн ые он а отдала сын овьям, котор ые р азделили их между собой также пор овн у. Каждый мальчик получил н а 2 ор еха больше, чем каждая девочка. Сколько у мамы дочер ей и сын овей? Сн ачала можн о выделить следующую часть условия: «Собр али в лесу 70 ор ехов. Половин у всех ор ехов мама р аздала дочер ям, остальн ые - сын овьям». Отсюда узн аем, что все дочер и получили 70 : 2 = 35 (ор .) и сын овья также получили 35 ор ехов. [5] Затем выделяется втор ая часть условия: «В семье 12 детей. Все дочер и получили 35 ор ехов. И все сын овья получили 35 ор ехов. Мальчики и девочки р азделили ор ехи пор овн у». Отсюда заключаем, что число сын овей и число дочер ей - это числа, котор ые в сумме дают число 12, и число 35 делится н а каждое из н их без остатка. Таким обр азом, мы пер ефор мулир овали условие, сказали его др угими словами. Тепер ь будем использовать способ подбор а. Число 35 делится н а 5, 7, 1, 35. Подходят числа 5 и 7, так как их сумма р авн а 12. Остается р ешить, кого было 5 - сын овей или дочер ей? Используем последн юю часть условия: «Каждый мальчик получил н а 2 ор еха больше, чем каждая девочка». Все девочки получили 35 ор ехов, все мальчики получили 35 ор ехов, если каждому мальчику досталось ор ехов больше, зн ачит, мальчиков мен ьше, чем девочек. Получаем ответ задачи: в семье 5 сын овей и 7 дочер ей. После р аботы, пр оведен н ой н а пер вом этапе, можн о пер ейти ко втор ому, н а котор ом учащиеся самостоятельн о р ешают н естан дар тн ые задачи. Пр иведем пр имер ы н естан дар тн ых задач. Задача 31. В магазин е р асфасовали кар тофель в 16 пакетов по 5 кг и по Зкг. Масса всех пакетов по 5 кг оказалась р авн ой массе всех пакетов по 3 кг. Сколько было пакетов по 5 кг и сколько было пакетов по 3 кг? (6 пакетов по 5 кг и 10 пакетов по 3 кг.) [4] Задача 32. Мама испекла пир ожки. Утр ом он а съела 1 пир ожок, а половин у всех оставшихся пир ожков положила в кор зин ку Кр асн ой Шапочке, чтобы он а их отн есла бабушке. По дор оге Кр асн ая Шапочка съела 2 пир ожка и тр етью часть оставшихся пир ожков отдала Волку. Бабушке Кр асн ая Шапочка пр ин есла 8 пир ожков. Сколько пир ожков испекла мама? (29 пир ожков.) Задача 33. Пер иметр тр еугольн ика р авен 18 см. Пер вая стор он а н а 4 см кор оче втор ой, а втор ая н а 1 см кор оче тр етьей. Н айди длин у каждой стор он ы тр еугольн ика, если длин ы выр ажаются целым числом сан тиметр ов. (3 см, 7 см, 8 см) Задача 34. У двоих мальчиков было вместе 8 гр уш. Когда один мальчик съел гр ушу, а др угой - 3 гр уши, гр уш стало пор овн у. Сколько гр уш было у каждого мальчика? (3 и 5 гр уш.) Задача 35. Имеется 6 шар ов тр ех цветов. Желтых шар ов больше, чем кр асн ых, и зелен ых шар ов больше, чем кр асн ых. Сколько шар ов каждого цвета? (1 кр асн ый шар , 2 зелен ых и 3 желтых.) Задача 36. Мальчик считал камушки, н о потом забыл, сколько их было. Помн ил только, что, когда считал пар ами, один камушек был лишн им, когда считал по четыр е - тоже один камушек был лишн им. Когда считал по пять - н и одн ого лишн его камушка н е было. Сколько было камушков, если их больше 10, н о мен ьше 40? (25 камушков.) Задача 37. В тр ех клетках 8 кр оликов. В пер вой столько, сколько во втор ой, а в тр етьей столько, сколько в пер вой и во втор ой вместе. Сколько кр оликов в каждой клетке? (2, 2 и 4 кр олика.) Задача 38. За н есколько один аковых тетр адей заплатили 51 р убль. Сколько стоит 1 тетр адь, если их купили больше 10, н о мен ьше 50? Цен а тетр ади выр ажается целым числом р ублей. (3 р убля.) Задача 39. В токар н ом цехе завода вытачивают детали из металлических заготовок. Из одн ой заготовки получается 1 деталь. Пр и изготовлен ии деталей получаются стр ужки, котор ые пер еплавляются в н овые заготовки. Из стр ужек, получен н ых пр и изготовлен ии четыр ех деталей, выплавляется 1 н овая заготовка. Сколько деталей можн о сделать таким обр азом из 16 металлических заготовок? (21 деталь.) Задача 40. После того как 3 человека съели по один аковому кусочку тор та пр ямоугольн ой фор мы, длин а и шир ин а тор та умен ьшились в 2 р аза. Н а сколько еще человек хватит оставшегося тор та, если все будут есть такие же кусочки, как и пер вые 3 человека? (Оставшегося тор та хватит н а 1 человека.)[24] Задача 41. Н а площадке игр али 7 девочек и 2 мальчика. Сумма возр астов всех игр ающих составила 80 лет. Все девочки были одн огодки. Один акового возр аста были и мальчики. Когда в одн у гр уппу объедин ились 5 девочек, а в др угую все остальн ые, то оказалось, что суммы числа лет игр ающих в одн ой гр уппе и др угой стали р авн ыми. Какого возр аста были игр ающие? (Возр аст каждой девочки - 8 лет, возр аст каждого мальчика - 12 лет.) Здесь мы высказали только осн овн ые идеи по поводу соответствующей р аботы, пр ивели пр имер ы задач. Н о, по мн ен ию мн огих учителей, такая р абота может и должн а н ачин аться с 1 класса. |
