управление рисками инновационных преоктов. Диссертация по направлению подготовки 38. 04. 08 Финансы и кредит

• Название: Диссертация по направлению подготовки 38. 04. 08 Финансы и кредит
• Анкор: управление рисками инновационных преоктов
• Дата: 16.09.2020
• Размер: 172.93 Kb.
• Имя файла: churkin_am_upravlenie-riskami-innovacionnyh-proektov-v-mashinost.docx
• Тип: Диссертация; #138212
• страница: 14 из 15

Оценка проекта с учетом реальных опционов с применением биноминальной модели Кокса-Росса-Рубинштейна

Применение биноминальной модели Кокса-Росса-Рубинштейна, далее биноминальной модели, для оценки стоимости реальных опционов создает значительное преимущество в том, что позволяет нивелировать ограничение DCF и DTA методов, заключающееся в постоянстве ставки дисконтирования для каждого этапа проекта.

Смысл биноминальной модели заключается в риск-нейтральном подходе, при котором ставкой дисконтирования на всех этапах проекта является безрисковая ставка. Это становится возможным за счет замены вероятностей, полученных по результатам экспертной оценки, на риск-нейтральные вероятности, рассчитываемые по формулам 8 и 9.

Исходные данные для оценки первого опциона – на выход из проекта, с помощью биноминальной модели приведены в таблице 11.
Таблица 11. Исходные данные для оценки опциона на выход из проекта

Параметр	Обозначение	Значение
Текущая стоимость базисного актива	S	53 563 782р.
Цена исполнения опциона	K	27 041 673р.
Безрисковая ставка	r	9.155%
Стандартное отклонение	σ	56.72%

Первым шагом оценки реальных опционов с использованием модели Кокса-Росса-Рубинштейна является построение биноминального дерева изменения приведенной стоимости проекта.

Для опциона на выход из проекта дерево изменения приведенной стоимости проекта показано на рисунке 9.

Рис. 9 Дерево изменения приведенной стоимости проекта (опцион на выход из проекта, данные в руб.)
По формулам 4 и 5 рассчитаны условные вероятности роста и снижения: p_u = 0.835, p_d = 0.165.

Стоимости управленческих опционов, соответствующие первому и второму узлам второго периода биноминального дерева (S₁ и S₂ соответственно) рассчитаны как разница между приведенной стоимостью проекта и ценой исполнения опциона: C₁₁ = 33 833 194р, C₁₂ = 0р, так как цена исполнения опциона выше приведенной стоимости проекта.

Стоимость проекта с учетом опциона рассчитана по формуле: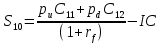
(22)
S₁₀ = NPV_p = – 1 149 075р.

Стоимость реального опциона на выход из проекта рассчитана как: C₀ = S₀ – NPV = 5 826 870р.

Таким образом, по результатам анализа эффективности проекта с учетом стоимости реального опциона на выход из проекта, оцененного с использованием биноминальной модели, проект не может быть рекомендован к осуществлению, так как имеет отрицательную чистую приведенную стоимость.

Далее с помощью биноминальной модели рассчитана стоимость второго опциона – на расширение проекта в третий год его реализации. Исходные данные для проведения расчетов приведены в таблице 12. Цена исполнения опциона на расширение проекта отличается от цены исполнения опциона на выход из проекта на 3 511 911р. – дисконтированную величину дополнительных затрат на увеличение производственных мощностей.
Таблица 12. Исходные данные для оценки опциона на расширение проекта

Параметр	Обозначение	Значение
Текущая стоимость базисного актива	S	59 081 798р.
Цена исполнения опциона	K	3 511 911р.
Безрисковая ставка	r	9.155%
Стандартное отклонение	σ	56.72%

Условные вероятности роста и снижения остаются такими же как для расчета первого опциона: p_u = 0.835, p_d = 0.165.

Для опциона на расширение проекта дерево изменения приведенной стоимости проекта показано на рисунке 10.

Рис. 10 Дерево изменения приведенной стоимости проекта (опцион на расширение проекта, данные в руб.)
Стоимости управленческих опционов, соответствующие первому и второму узлам второго периода биноминального дерева рассчитаны по тому же принципу, что для опциона на выход из проекта: C₂₁ = 65 074 298р, C₂₂ = 46 252 697р.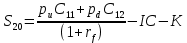
(23)
S₂₀ = NPV_c = 15 285 301р.
Стоимость реального опциона на расширение проекта равна: C₀ = S₂₀ – NPV = 8 359 306р.

Анализ проекта с учетом опциона на расширение, стоимость которого рассчитана с применением биноминальной модели, показал, что проект должен быть рекомендован к осуществлению. Опцион на расширение является приоритетным, так как он существенно увеличивает NPV проекта, создавая большой запас прочности.
В работе проведен анализ проекта с помощью DCF и DTA методов, и с использованием модели оценки стоимости реальных опционов. Результаты анализа являются эмпирическим подтверждением преимущества оценки инновационных проектов с учетом реальных опционов – возможных управленческих воздействий на результат проекта в случаях наступлениях рисковых событий.