управление рисками инновационных преоктов. Диссертация по направлению подготовки 38. 04. 08 Финансы и кредит
 Скачать 172.93 Kb. Скачать 172.93 Kb.
|
Биноминальная модель оценки реальных опционовПрименение метода ROV менеджерами компаний предполагает использование ими готовых моделей, в которые они могут подставлять значения переменных для оценки реальных опционов и принятия решений о целесообразности их реализации. Существующие модели оценки реальных опционов основаны на моделях оценки финансовых опционов. Наибольшее распространение в теории финансовых опционов получили биноминальная модель Кокса-Росса-Рубинштейна, модель Блэка-Шоулза, модель Уэйли, модель Блэка, модель Гармэна-Колхагена, модель Мертона. Для оценки реальных опционов были доработаны и внедрены в практику биноминальная модель и модель Блэка-Шоулза. Модели оценки реальных опционов в качестве переменных используют параметры опциона (цена исполнения, дата окончания), параметры базового актива (цена, волатильность) и процентную ставку. Биноминальная модель считается более простой, чем модель Блэка-Шоулза, так как ее использование предполагает, что в оцениваемой ситуации число и структура решений (число звеньев в дереве решений) известно. Биноминальная модель оценки опционов была предложена американскими экономистами Коксом, Россом и Рубинштейном в 1979 году. В основе биноминальной модели лежит использование имитирующего портфеля, состоящего из безрисковых займов и базового актива, для воспроизведения денежного потока, создаваемого оцениваемым опционом. Оценка стоимости опциона с помощью биноминальной модели начинается с построения схемы, отражающей процесс установления цены опциона. Каждому узлу схемы, или дерева, соответствует стоимость базового актива, рассчитанная с учетом предположений о наступлении некоторых событий и принятии определенных управленческих решений. Расчет стоимости реального опциона представляет собой движение от момента в будущем к настоящему моменту для приведения денежных потоков, которые будут созданы базовым активом, к сегодняшнему дню. На рисунке 4 показан общий алгоритм работы биноминальной модели. 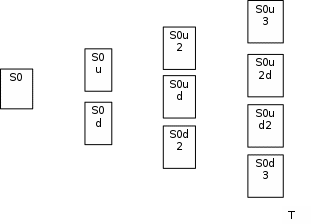 Рис. 4 Биноминальное дерево реальных опционов. S0 – приведенная к настоящему моменту стоимость базового актива; u – коэффициент роста; d – коэффициент снижения. На рисунке 5 показана эволюция стоимости базового актива, или, в контексте настоящей работы, инновационного проекта, за три периода. В узлах изображенного дерева стоят формулы расчета новых стоимостей проекта в будущих периодах: в каждый отрезок времени стоимость актива может двигаться вверх при благоприятном сценарии развития проекта или вниз при негативном сценарии. При оценке опционов биноминальным методом имитирующие портфели создаются для каждого периода осуществления проекта, то есть для каждого уровня биноминального дерева. При этом на всех этапах последовательной оценки, при движении по дереву от будущих периодов к настоящему, требуется принять наиболее эффективное управленческое решение. Аналогично построению дерева решений для базового актива может быть построено дерево решений для самого опциона. Для этого оценить опционы необходимо во всех узлах дерева. Далее приведены формулы расчета стоимости опционов CALL и PUT для биноминального дерева. 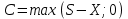 (5), (5),где C – стоимость опциона CALL; X – цена исполнения опциона. 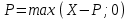 (6), (6),где C – стоимость опциона PUT. Компании выгодно исполнить опцион CALL, если цена его исполнения меньше спот цены, или рыночной цены, базового актива. Опцион PUT будет исполнен компанией, если, наоборот, цена исполнения больше спот цены базового актива. Стоимость реального опциона по биноминальному дереву с несколькими периодами может быть определена по формуле: 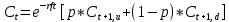 (7), (7),где Ct – стоимость реального опциона в период t; t – период исполнения опциона; p – вероятность роста; (1-p) – вероятность снижения; rf – безрисковая процентная ставка. Вероятность роста (p) можно определить по формуле:  (8), где (8), гдеru – доходность базового актива при росте; rd – доходность базового актива при снижении. Вероятность снижения (p-1) определяется, соответственно, по формуле: 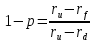 (9) (9)Таким образом, используя формулы (1) и (2) можно рассчитать стоимости опционов, начиная с последнего периода биноминального дерева. Стоимость опциона в любом периоде может быть определена с помощью формулы (3). Для того чтобы провести оценку опциона в настоящий момент требуется применение имитирующего портфеля, стоимость которого в соответствии с принципом арбитража равняется стоимости опциона. Стоимость имитирующего портфеля определяется по формуле: 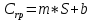 (10), (10),где b – количество заимствованных единиц безрискового актива; m – количество единиц базового актива. Для следующего периода стоимость имитирующего портфеля, равная стоимости опционов, может быть рассчитана по формулам: 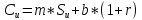 (11) (11)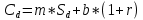 (12) (12)Решение системы уравнений из формул (7) и (8) позволяет определить количества единиц заимствованного безрискового актива и базового актива: 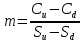 (13) (13)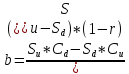 (14) (14)Стоимость реального опциона равна стоимости имитирующего портфеля и определяется по формуле: 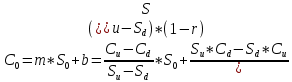 (15) (15)Оценка стоимости реального опциона с применением биноминальной модели предполагает расчет относительных показателей роста и снижения по следующим формулам: 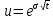 (16), (16),где σ – волатильность, стандартное отклонение, денежного потока. 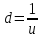 (17) (17)Биноминальная модель относится к сложным моделям оценки стоимости реальных опционов, но она имеет существенные преимущества: высокая точность результатов при большом количестве периодов принятия управленческих решений и нескольких источниках неопределенности. |
