|
|
Урусова Я.А._Мм-1401. Формирование критического мышления при обучении математике учащихся общеобразовательной школы
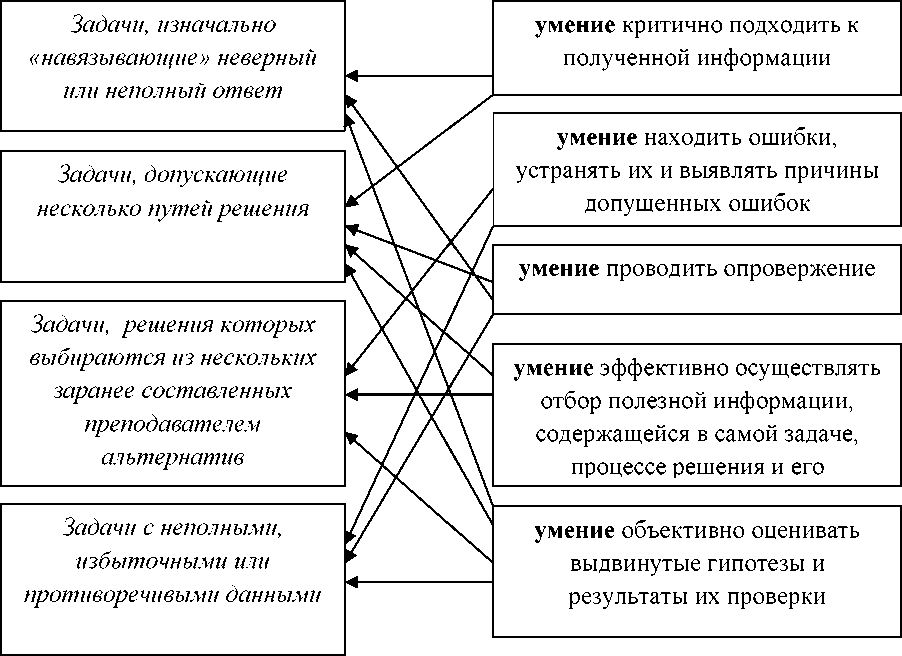
Соответствие различных видов математических
задач и умений критически мыслить (по Е.Г. Журавлевой)
О.В. Андронова предлагает применять на уроках математики технологию развития критического мышления учащихся посредством чтения и письма, разработанную американскими педагогами Дж. Стил, К. Мередитом и Ч. Темплом в середине 90-х годов XX века и используемую в основном традиционно при изучении гуманитарных дисциплин. Одна из основных целей данной технологии - научить ученика самостоятельно мыслить, осмысливать, структурировать и передавать информацию, чтобы 27
другие узнали о том, что новое он открыл для себя. Кроме того, данной технологии присущи различные элементы творчества (эссе, синквейн и т.д.), которые способствуют повышению интереса учащихся к урокам математики, познавательной активности, учебной мотивации и т.д.
Автор подчеркивает, что в данной технологии в процесс обучения включен каждый школьник, а не часть ученического коллектива, что способствует их более качественному, а не поверхностному обучению [1].
Н.Ф. Плотникова связывает формирование критического мышления с процессом обучения и воспитания.
На основе изучения этапов и способов формирования критического мышления Н.Ф. Плотниковой представлена модель формирования критического мышления студентов вузов [50].
В монографии А.В. Федорова [64] представлены результаты анализа научных трудов зарубежных и отечественных ученых по формированию критического мышления учащихся.
Определение уровня развития критичности - важное условие выбора педагогических технологий, методов формирования и развития мышления обучающихся.
Чаще всего у младших школьников различают три уровня проявления критичности мышления [3]: зарождающейся критичности - школьник замечает то, что в изображении объекта познания допущены ошибки, но он еще не может их осмыслить, пояснить; статирующей критичности - ученики находят допущенные в объекте познания ошибки, но не стараются выявить причину их возникновения; корригирующей критичности - учащиеся не только отражают части, компоненты объекта познания во взаимосвязи взаимозависимости и замечают допущенные в них ошибки, но и выявляют причины их появления, а также указывают пути и средства их устранения.
Таким образом, зная методы определения уровня критичности мышления учащихся общеобразовательной школы, необходимо рассмотреть различные приемы и средства формирования критичности мышления
28
учащихся общеобразовательной школы, которые будут раскрыты в следующем параграфе.
Различные приемы и средства формирования критического
мышления учащихся общеобразовательной школы
при обучении математике
По мнению С.В. Лаптинской, что технология развития критического мышления подразумевает привлечение обучаемых к различным способам и приемам оценочной деятельности (самооценка, взаимооценка). Используя технологию критического мышления, педагог создает такие ситуации, проживая которые учащийся осознал бы себя в обществе в большой степени. Ситуация выбора, диалог, работа в группе, дискуссия - учебные ситуации, обычные для формирования критического мышления [25].
Обучение критическому мышлению нужно воспринимать как одну из базовых форм подготовки к успешной жизнедеятельности в информационном и постинформационном обществе [61].
К педагогическим средствам формирования критического мышления отнесены [70]:
включение в образовательные стандарты и программы целей развития мышления и обогащения содержания, которые способствуют условиям становления критичности ума;
выделение профессиональных компетенций и системы умений и навыков логически и критически мыслить;
подготовка учителей, направленная на овладение профессиональными компетенциями в области логического и критического мышления и знаниями о методах и способах их формирования;
координация исследований в области развития мышления и обмен опытом исследователей и учителей об инновациях в технологиях формирования критического мышления путем публикаций, конференций, семинаров, мастер-классов и специальных проектов.
29
Е.А. Ходос и А.В. Бутенко предлагают использовать на уроках «дидактические игры с использованием техник критического мышления» [61].
Формирование данного типа мышления более эффективно при одновременном развитии логического мышления [38].
В.А. Попков и А.В. Коржуев используют классические приемы формирования критического мышления (диспут, рецензирование и оппонирование) [49].
Д.М. Шакирова приводит четыре этапа формирования критического мышления [70]: 1) актуализация знаний, пробуждение интереса, любознательного отношения к теме, определение целей изучения материала; 2) осмысление новой информации, критическое чтение и письмо; 3) размышление, или рефлексия, формирование личного мнения и отношения к материалу; 4) обобщение и оценка информации, проблемы, способов ее решения и проявление собственных возможностей.
Е.П. Мельникова рекомендует применять следующие приемы технологии критического мышления [37]:
1. Написание эссе - еще один современный прием технологии критического мышления, который позволяет раскрыть интересующую тему и подчеркнуть собственное мнение, возникшее после работы с наглядными источниками информации.
2. Технология «Портфолио» помогает обучающимся не только самоопределяться в изучаемом предмете, но и делать практические выводы в любой жизненной ситуации, то есть реализовывать собственную индивидуальность. Портфолио может включать в себя не только материалы студенческих работ, но и листы наблюдения, фрагменты эссе, видеозаписи, проекты и планы выступлений, компьютерные презентации.
Дидактическая модель формирования критического мышления охватывает характеристику деятельности обучаемого, которая включает
30
методику работы с информацией, формы, методы и приемы учения и самооценки.
В качестве примера Д.М. Шакирова приведены такие возможные методы и приемы формирования критического мышления, как [70]:
самоанализ и самооценка уровня собственной готовности к критическому усвоению материала и анализ критического потенциала проблемы;
сочетание репродуктивного и частично-поискового методов учения при выполнении учебных заданий и различных видов критики (критика- аналогия, критика-похвала, критика-озабоченность и т.п.);
поисковые методы учения, которые применяются при выполнении творческих работ;
перенос методов и приемов критического анализа в новые ситуации;
применение мыслительных компетенций при выполнении самостоятельных работ (рецензирование, разрешение критических ситуаций, анализ данных Интернет - источников, книг, публичных выступлений и т.п.).
В Мозырском государственном областном лицее учителями предлагается использовать в работе различные методы и приемы для развития критичности мышления учащихся: мозговой штурм; инсерт; ролевая игра; свободное письмо; синквейн; кластер; взаимоопрос; перекрестная дискуссия [35].
Так, под кластером в методической литературе [1] понимают графический наглядный способ формирования материала (таблица, схема); под инсертом - способ работы с текстом, который подразумевает использование определенных пометок («+» - ранее известное; «А» - новое; «?» - вызывает затруднение); синквейном - метод краткого описания урока с помощью ключевых слов.
Таким образом, в данном параграфе рассмотрены различные приемы и средства формирования критического мышления учащихся общеобразовательной школы при обучении математике. Возникает вопрос
31
рассмотрения методики организации обучения математике с помощью определенных видов заданий, направленных на формирование критичности мышления у учащихся.
§ 4. Организация обучения математике учащихся с помощью задач
на развитие критичности мышления
Учебная задача существенно отличается от многочисленных частных задач, входящих в программу того или иного класса при традиционном обучении. При решении учебной задачи школьник первоначально овладевает общим способом решения частных задач на уровне теоретического обобщения. Задача решается для всех однородных случаев сразу. Разрешение учебной задачи всегда заканчивается построением программы, предписания, алгоритма - получением ориентировочной основы для решения сходных задач. Эта ориентировочная основа является основанием для анализа условия, планирования, осуществляемых учеником при решении задач, для рефлексивных действий, для развития соответствующих особенностей мышления, которые являются показателем развитого мышления [8].
Как показывает практика работы в школе, математику любят в основном те ученики, которые умеют решать задачи. Следовательно, научив детей владеть умением решать задачи, мы окажем существенное влияние на их интерес к предмету, на развитие их мышления.
Напомним, что кроме классификации задач при обучении математике, представленные выше в §1, задачи делят на стандартные и нестандартные. Нестандартная задача - это задача, решение которой не является для решающего известной цепью известных действий, способствуют развитию логического мышления. Для ее решения учащийся сам должен изобрести (составить, придумать) способ решения.
Так, Ю.М. Колягин раскрывает это понятие следующим образом: «Под нестандартной понимается задача, при предъявлении которой учащиеся не
32
знают заранее ни способа ее решения, ни того, на какой учебный материал опирается решение» [23].
Т.И. Лябина предлагает при обучении математике использовать следующую нестандартную задачу для развития критичности [28]:
Задача. На день рождения Малыша фрекен Бок испекла торт. Малыш и торт весили столько же, сколько Карлсон и фрекен Бок. Когда торт съели, Карлсон весил столько же, сколько фрекен Бок и Малыш. Докажите, что Карлсон съел кусок торта, весивший столько же, сколько фрекен Бок до дня рождения.
Решение: Т+М = К+Б. Кт+Тб+Тм+М=К+Б. К+Тк = Б+Тб +М+Тм. Прибавим к обеим частям Тк. К+2Тк =Б+М+Тк+Тм+Тб. К+2Тк=Б+М+Т. т.к. Т+М=К+Б, то К+2Т=К+2Б. 2Т=2Б. Т=Б. ч.т.д.
Из нестандартной задачи, представленной Т.И. Лябиной для развития критичности видно, что автором используются логические операции анализа и синтеза, а также прием составления алгоритма при решении задач.
Н.В. Загурская предлагает для формирования критичности мышления школьников использовать на уроках математики задачи умение анализировать, развитие наблюдательности, самоконтроля.
Автор приводит задания, связанные с темой «Одночлен», которую изучают в 7-м классе [17]:
Задание 1. Выпишите выражения, которые могут быть преобразованы с помощью формулы квадрата суммы:
1) (х-3)(х-3); 2) (2а-5,7Ь)2а; 3) (а-5)(а + 5); 4) (1-а)4;
5) (х2 + y2)2; 6) (d-2)(2-d); 7) (3m + 4n)2; 8) (1,2 - 5xy6)2;
9) (5а-2Ь + 6с)(6с + 5а-2Ь); 10) (-5m - 2,2n)2.
По каким признакам вы выделяли выражения?
Чтобы ваш опыт не пропал даром, составьте памятку для распознавания таких выражений, которые являются квадратами суммы. Сравните вашу памятку со следующей (Рис.1):
33

Рис.1
Отметим, что данное задание может использоваться в 7 классе при изучении темы «Квадрат суммы» после объяснения нового материала.
Задание 2. Составьте два выражения, которые по формуле квадрата суммы преобразовать нельзя.
Обратили ли вы внимание на то, что в прочитанном параграфе много задач, связанных с понятием признака? Что такое признак, вы можете подробнее узнать из беседы психолога «Что такое признак?»
Как видно, данное задание предназначено для работы с учебником, с помощью него у учащихся формируется уметь анализировать и находить в тексте главное.
Задание 3. Представим характерные портреты некоторых одночленов. К заданию выдаются карточки, представленные ниже на Рис.2.
Рассмотрите портреты и вставьте пропущенные слова в следующих определениях: 1. Одночлен, в котором единственный числовой множитель стоит на первом месте и степень любой переменной входит множителем только один раз, называется одночленом ... вида. 2. Сумма показателей всех степеней переменных называется ... одночлена. 3. Числовой множитель одночлена стандартного вида называется . одночлена. 4. Одночлены, буквенные части которых равны, называются . одночленами.
Проверьте себя. Вставленные вами слова должны находиться среди следующих: "стандартный", "нулевой", "степень", "подобные",
"коэффициент", "дробь".
34
Каждый ли одночлен можно привести к стандартному виду?
Проанализируйте процесс приведения к стандартному виду одночлена 25a3bc(0,2)a2cb2.

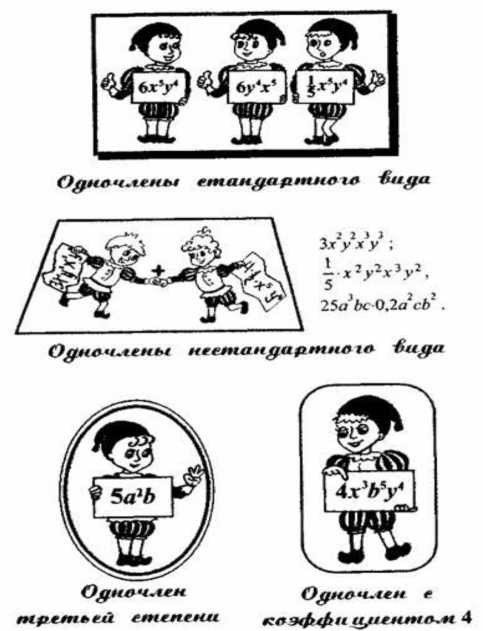

Рис.2
35
Как отмечает Н.В. Загурская, в ходе выполнения задания согласно определения для приведения одночлена к стандартному виду необходимо сгруппировать все числовые множители, затем все степени с одинаковым основанием и выполнить соответствующие умножения. 25а3Ьс(0,2)а2сЬ2 = (25 * 0,2)(а3 * а2')(Ь ** Ь2)(с * с) - на основе коммутативного и ассоциативного свойств умножения; (25 * 0,2)(а3 * а2)(Ь * Ь2)(с * с) = 5 * а5 * Ь3 * с2 - по основному свойству степени. Итак, 5 * а5 * Ь3 * с2 -
стандартный вид исходного одночлена 25а3Ьс(0,2)а2сЬ2.
Автор рекомендует при решении данного задания обратить внимание, насколько проще стандартный вид одночлена по сравнению с исходным. Преобразуя одночлен, фактически получает алгоритм приведения любого одночлена к стандартному виду [17].
Таким образом, в заданиях 1-3, предложенные Н.В. Загурской, для развития критичности мышления учащихся 7 классов используются в основном задания: а) на формирование условия задачи по типу «вопрос- ответ»; б) на восприятие на слух; в) содержащие задачи на развитие различных мыслительных умений (анализ).
Вместе с тем, одним из ценных дидактических средств развития критичности мышления школьников являются математические софизмы, которые можно использовать как с первых ступеней обучения, так, и, на протяжении дальнейшего обучения.
Софизмы - ложные результаты, полученные с помощью рассуждений, которые только кажутся правильными, но обязательно содержат ту или иную ошибку [30].
Софизмы выбираются в зависимости от дидактических целей обучения учащихся и этапа усвоения учебного материала.
Математический софизм тем более замысловат, чем более тонкого характера ошибка в нём проводится, чем менее она предупреждена обычным школьным курсом [9].
Разбор софизма разбивают на два этапа:
36
|
|
|
 Скачать 280.63 Kb.
Скачать 280.63 Kb.




