Урусова Я.А._Мм-1401. Формирование критического мышления при обучении математике учащихся общеобразовательной школы
 Скачать 280.63 Kb. Скачать 280.63 Kb.
|
задании 5 части 1«Простейшие уравнения» есть раздел с заданиями на тему «Логарифмические уравнения», в котором рассматривается много заданий по теме исследования, например, такие как [52]:1. Найдите корень уравнения log5(5 — х) = log53. Так как логарифмы имеют одинаковые основания, то получаем 5 - х = 3, отсюда следует, что х=2. 2. Решите уравнение loqx-549 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них. Решение: на ОДЗ перейдем к уравнению на основание логарифма: lOq ч49 = 2 ^ { (Х — 5)2 = 49, ^ { Х — 5 = ±7, ^ q%-5 2 {х —5>0,х —5*1 {х — 5>0,% — 5*1 ^ x - 5 = 7 ^ x = 12. Итак, на ОДЗ уравнение имеет только один корень. Ответ: 12. В задании 13 (С1) части 2 «Уравнения» есть раздел на тему «Логарифмические и показательные уравнения», рассмотрим одно из заданий [52]: Решите уравнение loq5(2 — х) = loq25x4 . Укажите корни этого уравнения, принадлежащие отрезку [loq9 —; loq98]. 82 Решение. Запишем исходное уравнение в виде: 44 1од5(2 - х) = 1од5Х2 « {х2 = 2 - х’ « {(х + 2) * О - D = О, 5 55 I х2 > О, I х Ф 0. Получим, что х= - 2 или х=1. Поскольку 1од9 — < —2 < 1од98 < 1, получаем, что отрезку [1од9 —; 1од98] 8 8 8 82 8 8 • 8 8 82 принадлежит единственный корень -2. Ответ: -2. В задании 18 (С6) части 2 «Задача с параметром» содержит раздел «Уравнения с параметром», в котором присутствуют задания с логарифмами, например [52]: Определите, при каких значениях параметра а уравнение lx — 2| = а1од21х — 2| имеет ровно два решения. Решение. Пусть |х - 2| = t, тогда t = а1од21, t > 0 .Чтобы исходное урав- нение имело ровно два решения, уравнение t = а1од21 должно иметь един- ственное решение. Если a = 0, то уравнение не имеет решений. Если a < 0 , то уравнение имеет единственное решение (см. рис.3). Если a > 0, уравнение имеет единственное решение тогда и только тогда, когда прямая y = t касается графика функции у = а.1од21 (см. Рис.3 ниже), что задаётся системой соотношений: а 1п2' (а = tln2, (а = eln2, alnt ^ { Int = 1, { t = e. Т2/ Заметим, что найденное значение параметра, действительно, положительно. Ответ: a<0, a= e ln2. I. a 1 =—-. tln2 ^ t = а1од21, t p' = (alog2ty ^ f t = а1од21 45 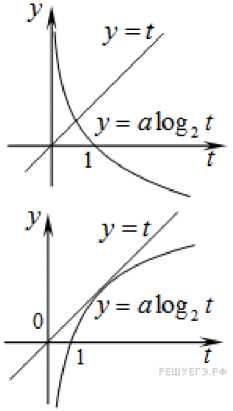 Рис.3 Тема «Логарифмическая функция» В ФГОС среднего (полного) общего образования представлены требованиях к предметным результатам освоения образовательной программы по математике на базовом и углубленном уровнях у учащихся: на базовом уровне [63]: сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира; сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий; владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач; владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств; 46 сформированность представлений об основных понятиях, идеях и методах математического анализа; владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием; сформированность представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин; владение навыками использования готовых компьютерных программ при решении задач. на углубленном уровне сформированность представлений о необходимости доказательств при обосновании математических утверждений и роли аксиоматики в проведении дедуктивных рассуждений; сформированность понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач; сформированность умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат; сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей; владение умениями составления вероятностных моделей по условию задачи и вычисления вероятности наступления событий, в том числе с 47
|
