Машфак. ТВ иМС для МСФ. Исследование связи между показателями, часть из которых являются случайными

• Название: Исследование связи между показателями, часть из которых являются случайными
• Анкор: Машфак
• Дата: 18.11.2022
• Размер: 2.07 Mb.
• Имя файла: ТВ иМС для МСФ.doc
• Тип: Исследование; #795733
• страница: 4 из 11

4. Для полученной реализации выборки подсчиты-

вают значение критерия, т.е.

5. Если ( например, для правосторонней области ), то нулевую гипотезу отвергают; если же ( ), то нет оснований, чтобы отвергнуть гипотезу

Критерий согласия Пирсона – наиболее часто употребляемый критерий для проверки простой гипотезы о законе распределения.

Предположим, что по виду графика статистического распределения

или из каких-либо других соображений, удается выдвинуть гипотезу о множестве функций определенного вида (нормальных, показательных, биномиальных и т.п.), к которому может принадлежать функция распределения исследуемой случайной величины Х. Критерий² Пирсона позволяет производить проверку согласия эмпирической функции распределения с гипотетической функцией распределения F₀(x).

Для проверки гипотезы поступают следующим образом (например,

для непрерывной случайной величины):

• разбивают всю область значений случайной величины на l интервалов

• на основании гипотетической функции F(x) вычисляют вероятность попадания СВ Х (т.е. наблюдения ) в частичные интервалы =

(i =1, 2, ..., l);

• умножая полученные вероятности p_i на объем выборки n, получают теоретические частоты np_iчастичных интервалов ,т.е. частоты, которые следует ожидать, если гипотеза справедлива;

• имеем статистический ряд распределения случайной величины

			…
			…

и теоретический ряд распределения:

		…
		…

Если эмпирические частоты m_i сильно отличаются от теоретических

, то проверяемую гипотезу следует отвергнуть; в противном случае – принять.

• вычисляют выборочную статистику (критерий) ²: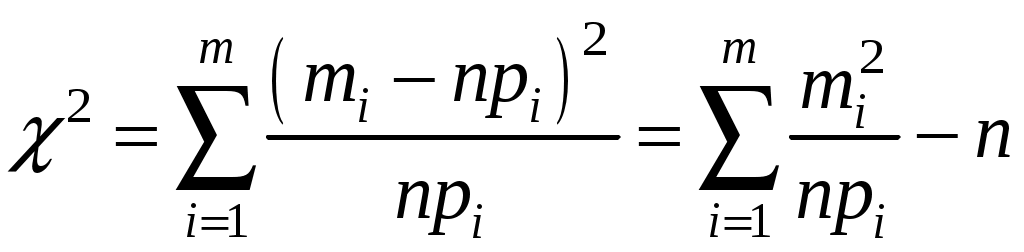

.

В качестве меры расхождения между и ( ) К.Пирсон (1857–1936; англ. математик, статистик, биолог, философ) предложил величину («критерий Пирсона») . Согласно теореме Пирсона, если гипотеза верна, то при статистика имеет -распределение с степенями свободы, где число групп (интервалов) выборки, число параметров предполагаемого распределения. Критерий ² сконструирован таким образом, что чем ближе к нулю наблюдаемое значение критерия ², тем вероятнее, что гипотеза справедлива. Поэтому для проведения гипотезы применяется критерий ² с правосторонней критической областью. Необходимо найти по таблицам квантилей ²-распределения по заданному уровню значимости  и числу степеней свободы  критическое значение удовлетворяющее условию

Правило применения критерия сводится к следующему:

1. 
   По формуле вычисляют – выборочное значение статистики критерия.
   
2. 
   Выбрав уровень значимости критерия, по таблице -распре-
   

деления находят критическую точку (квантиль)

3. Если ²_набл >²_;, то считается, что гипотетическая функция F₀(x) не согласуется с результатами эксперимента, т.е. гипотеза отвергается. Если ²_набл ²_;, то считается, что гипотетическая функция F₀(x) согласуется с результатами эксперимента.

Необходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений (т.е. ). Если в отдельных интервалах их меньше, то число интервалов надо уменьшить путем объединения (укрупнения) соседних интервалов.

Раздел 10. Корреляционно-регрессионный анализ

(двумерная модель)

При исследовании двух зависимых случайных величин X и Yзаме-чено, что известная функциональная зависимость встречается достаточно редко, ибо одна из них или обе подвержены воздействию других случай-ных факторов – в этом случае говорят о статистической зависимости, частным случаем которой и является корреляционная зависимость X и Y.

Корреляционной зависимостью Y от Xназывается функциональная за-висимость условной средней от : .

Это условие называется уравнением регрессии Y на X; функция называется регрессией Y на X, а её график – линией регрессии Y на X.

Аналогично определяется корреляционная зависимость X от Y: . Если обе функции регрессии и линейные, то корре-ляцию называют линейной; при этом обе линии регрессии являются пря-мыми линиями.

На практике часто используются выборочные уравнения линейной регрессии в виде или

Для определения параметров и в уравнении используется получаемая на основании метода наименьших квадратов система двух линейных уравнений:



откуда находятся выражения для и :

, (2.12)

Аналогично находятся параметры и для функции

Очень часто может интересовать не сама зависимость одной перемен-

ной от другой, а именно характеристика тесноты линейной связи между ними, которую можно было бы выразить одним числом. Эта ха-рактеристика называется выборочным коэффициентом линейной корреля-ции r:

, (2.13)

где выборочный корреляционный момент, S_x, S_y – выборочные стандарты величин X и Y соответственно.

Если r > 0, то корреляционная связь между переменными прямая, при r < 0 – обратная.

Свойства коэффициента корреляции r:

1⁰. .

В зависимости от того, насколько |r| приближается к единице, раз-личают связи:

|r| < 0,3 – слабая связь;

|r| = 0,3 – 0,5 – умеренная связь;

|r| = 0,5 – 0,7 – заметная (значительная) связь;

|r| = 0,7 – 0,8 – достаточно тесная связь;

|r| = 0,8 – 0,9 –тесная (сильная) связь;

|r| > 0,9 – очень сильная связь.

2⁰. При |r| = 1 – функциональная зависимость y = f(x).

3⁰. Чем ближе |r| к нулю, тем слабее связь.

4⁰. При r = 0 линейная корреляционная связь отсутствует.

5⁰. r_xy= r_yx – случайные переменные симметричные.

6⁰. Если все значения переменных увеличить (уменьшить) на одно и то же число или в одно и то же число раз, то величина коэффициента кор-реляции не изменится.

Выборочный коэффициент корреляции служит оценкой своего генерального параметра.

Чтобы выяснить, находятся ли случайные величины X и Y генераль-ной совокупности в линейной корреляционной зависимости, надо проверить значимость r. Для этого проверяют нулевую гипотезу о равенстве

нулю коэффициента корреляции генеральной совокупности Н₀: =0, т.е.

линейная корреляционная связь между признаками X и Y случайна. Выдвигается альтернативная гипотеза Н₁: 0, т.е. линейная корреляционная связь между признаками X и Y имеется.

В качестве критерия проверки гипотезы Н₀ принимается случайная величина

.

Величина t при справедливости Н₀ имеет распределение Стьюдента (t-статистика) с = n–2 степенями свободы.

Сравнивая наблюдаемое значение критерия t с критическим значе-нием t_кр, определяемым по таблице по заданному уровню значимости  и по числу степеней свободы, имеем:

 если |t_набл| <t_кр = t_{2; n-2}, то Н₀ принимается, т.е. нет линейной кор-реляционной связи между переменными;

 если |t_набл| t_кр, то Н₀ отвергается в пользу Н₁, т.е. имеется ли-нейная корреляционной связь между переменными.


3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ И

РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
3.1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Пример 3.1. Слово МАТЕМАТИКА составлено из карточек, на каж-дой из которых написана одна буква. Затем карточки смешивают и выни-мают без возврата по одной. Найти вероятность того, что буквы вы-нимают в порядке заданного слова.

Решение.

1-й способ. Событие состоит в получении нужного слова МАТЕМАТИКА. Возможным исходом является полученная последовательность букв, общее число которых . Некоторые буквы в слове повторяются (М-два раза, А-три раза, Т-два раза), поэтому возможны перестановки, при которых слово не изменяется. Их число равно . Таким образом, по формуле (1): .

2-й способ. Укажем события:

А₁- вынута карточка с буквой М;

А₂- вынута карточка с буквой А;

…………………………………….

А₁₀ –вынута карточка с буквой А.

Тогда события и связаны соотношением . События зависимы, т.к. карточки вынимаются без возврата. Поэтому

.