Машфак. ТВ иМС для МСФ. Исследование связи между показателями, часть из которых являются случайными
 Скачать 2.07 Mb.
|
|
Пример 3.2. В магазине выставлены для продажи 20 изделий, среди которых 4 изделия некачественные. Какова вероятность того, что взятые случайным образом 3 изделия будут некачественными? Решение. Рассмотрим событие  - среди взятых случайным образом трёх изделий оказалось три некачественных. Число исходов m, благоприятных свершению события , определяется по формуле  . Число всех возможных испытаний n определим так:  . Тогда вероятность события найдём по формуле классической вероятности (1): .Пример 3.3. Пусть вероятность того, что забег выигрывает Николай, равна  , а вероятность того, что забег выигрывает Пётр, равна  . Какова вероятность того, что забег выиграет один из них?Решение. Введём события: А – забег выигрывает Николай, В – забег выигрывает Пётр, С – забег выиграет один из них. Так как события А и В несовместны, то С = А + В. Тогда по теореме сложения вероятностей имеем:  Пример 3.4. На сборку поступают детали из трёх цехов в отношении 1:3:6. Количество бракованных деталей в продукции цехов соответст-венно равно 5%, 2%, 8%. Определить вероятность того, что: а) наудачу взятая деталь окажется бракованной; б) оказавшаяся бракованной деталь изготовлена во втором цехе. Решение. В качестве гипотез будем рассматривать события  состоящие в том, что взятая наудачу деталь изготовлена i-м цехом. Вероятности этих событий получим по формуле  , если в ка-честве n принять сумму всех частей, а в качестве m – соответствующее количество частей для данного цеха. Используя условия примера, имеем:  Событие А состоит в том, что взятая наудачу деталь – бракованная. Условные вероятности равны:  После описания исходных данных можно ответить на поставленные условием примера вопросы: а) по формуле полной вероятности имеем:  б) используя формулу Байеса  , получим:  Пример 3.5. Дано распределение дискретной случайной величины X:
Найти математическое ожидание, дисперсию (сравнить значения по двум формулам) и среднее квадратичное отклонение. Решение. Математическое ожидание найдём по формуле:  . Дисперсию подсчитаем сначала по формуле:  .Сделаем проверку, подсчитав по другой формуле:  .Ответы совпали. Среднее квадратичное отклонение определим по формуле  .Пример 3.6. В городе имеются 2 оптовые базы. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна 0,3. Составить ряд распределения числа баз, на которых искомый товар отсутствует в данный момент. Решение. Случайная величина Х распределения числа баз, на кото-рых искомый товар отсутствует, имеет биномиальное распределение с параметрами 0,3 и 2. Она принимает целочисленные значения от 0 до 2 с вероятностями  :  , , .Проверим, выполнено ли основное свойство вероятностей:  . Составим ряд распределения вероятностей случайной величины X:
Пример 3.7. Непрерывная случайная величина 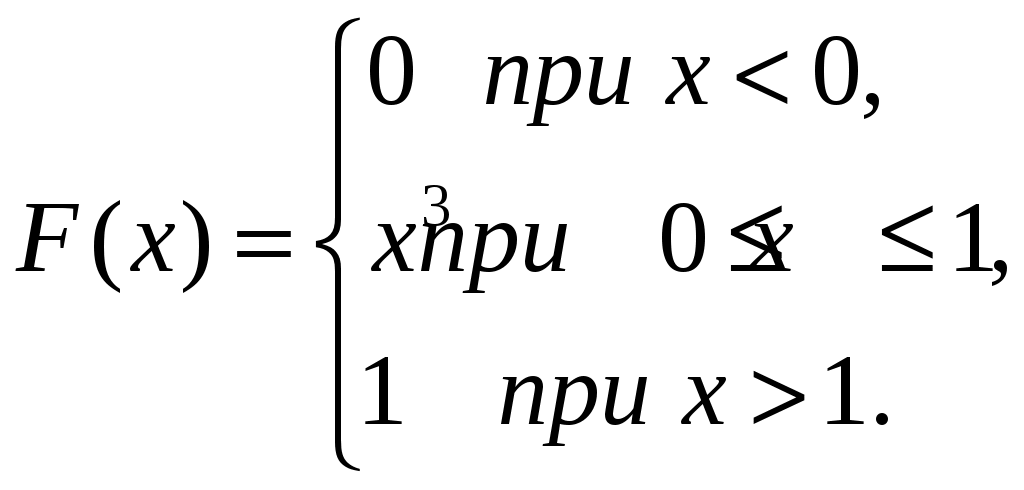 задана интеграль-ной функцией распределения: Требуется: 1. Найти дифференциальную функцию (плотность вероятности)  .2. Найти математическое ожидание  и дисперсию  .3. Построить графики интегральной и дифференциальной функций. Решение. 1. Воспользуемся формулой 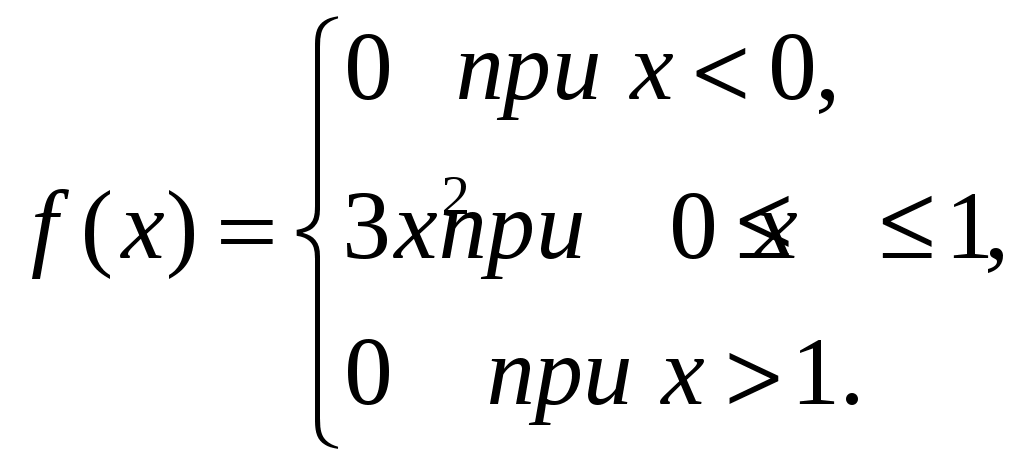  2. Если непрерывная случайная величина  задана функцией , то её математическое ожидание определяется формулой  .Так как функция при  и при  равна нулю, то из пос-ледней формулы имеем: .Дисперсию  определим по формуле  . Тогда  Замечание. Дисперсию можно определить и по формуле  .3. Графики функций 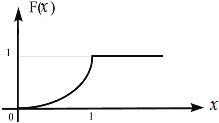 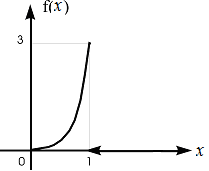и изображены на рис. 3.1 и 3.2.  Рис. 3.1. Интегральная кривая Рис. 3.2. Дифференциальная кривая Пример 3.8. Непрерывная случайная величина имеет нормальное рас- пределение. Её математическое ожидание равно 9, среднее квадратичное отклонение – 2. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (6,10). Решение. Используем формулу (2), учитывая, что M(X) = 9,   По таблице значений функции Лапласа (Приложение 1) находим  ,  . После подстановки получаем значение искомой вероятности:  .Пример 3.9. Множество состояний студентов некоторого вуза с пятилетним сроком обучения следующее: Sl – первокурсник, S2 – второкурс-ник, ... , S5 – выпускник. Студенты могут выбывать из вуза в результате его окончания или отчисления, поэтому дополним систему следующими состояниями: S6 – специалисты, окончившие вуз; S7– лица, обучавшиеся в данном вузе, но не окончившие его. Решение. Для множества учащихся вуза теперь все возможные состояния перечислены. Составим матрицу переходов из одного состояния в другое, предпо-лагая, что исключенные не могут быть восстановлены. Из состояния S1(первокурсник) за год возможны переходы в состоя-ние S2(второкурсник), S1 (остаться на первом курсе) и S7 (выбыл из вуза). Остальные переходы считаем невозможными. Поэтому первая строка матрицы состоит из трех положительных чисел: р1 – вероятности выбыть из института, r1 – перейти на II курс; q1–остаться на Iкурсе; причем p1+r1+q1=1. Осталь-ные вероятности перехода из состояния S1 в другие равны нулю. Для второкурсника (состояние S2)возможны переходы в состояния S3, S2,S7 с вероятностями r2,q2, p2соответственно. Аналогично для состоя-ний S3,S4и т.д. Построим граф состояний данной цепи Маркова и разметим его пере-ходными вероятностями, отличными от нуля (рис. 3.3): 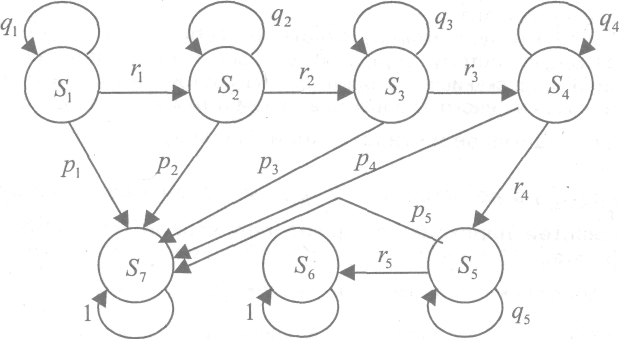 Рис. 3.3. Граф состояний цепи Маркова Составим матрицу вероятностей переходов:
P= |