Машфак. ТВ иМС для МСФ. Исследование связи между показателями, часть из которых являются случайными

• Название: Исследование связи между показателями, часть из которых являются случайными
• Анкор: Машфак
• Дата: 18.11.2022
• Размер: 2.07 Mb.
• Имя файла: ТВ иМС для МСФ.doc
• Тип: Исследование; #795733
• страница: 3 из 11

А. Дискретные случайные величины. Пусть X–дискретная случайная величина, которая в результате п опытов приняла возможные значения х₁, х₂,... , х_п. Допустим, что вид закона распреде­ления величины Xзадан, но

неизвестен параметр θ, которым определяется этот закон. Требуется най-

ти его точечную оценку θ* = θ*(х₁, х₂, ... , х_п).

Обозначим вероятность того, что в результате испытания вели­чина Xпримет значение х_i через р (x_i; θ).

Функцией правдоподобия дискретной случайной величины Xназывают

функцию аргумента θ: L(x₁, x₂, ..., x_n; θ) = р(x₁; θ)  р(x₂; θ)  ...  р(x_n; θ).

Оценкой наибольшего правдоподобия параметра θ называют такое его значение θ*, при котором функция правдоподобия дости­гает максимума.

Функции L и 1nLдостигают максимума при одном и том же значении θ, поэтому вместо отыскания максимума функции L ищут, что удобнее, максимум функции 1nL (логарифмическая функция правдоподобия).

Точку максимума функции 1nL аргумента θ можно искать, на­пример, так:

1. Найти производную .

2. Приравнять производную нулю и найти критическую точку θ* – корень полученного уравнения (уравнения правдоподобия).

3. Найти вторую производную 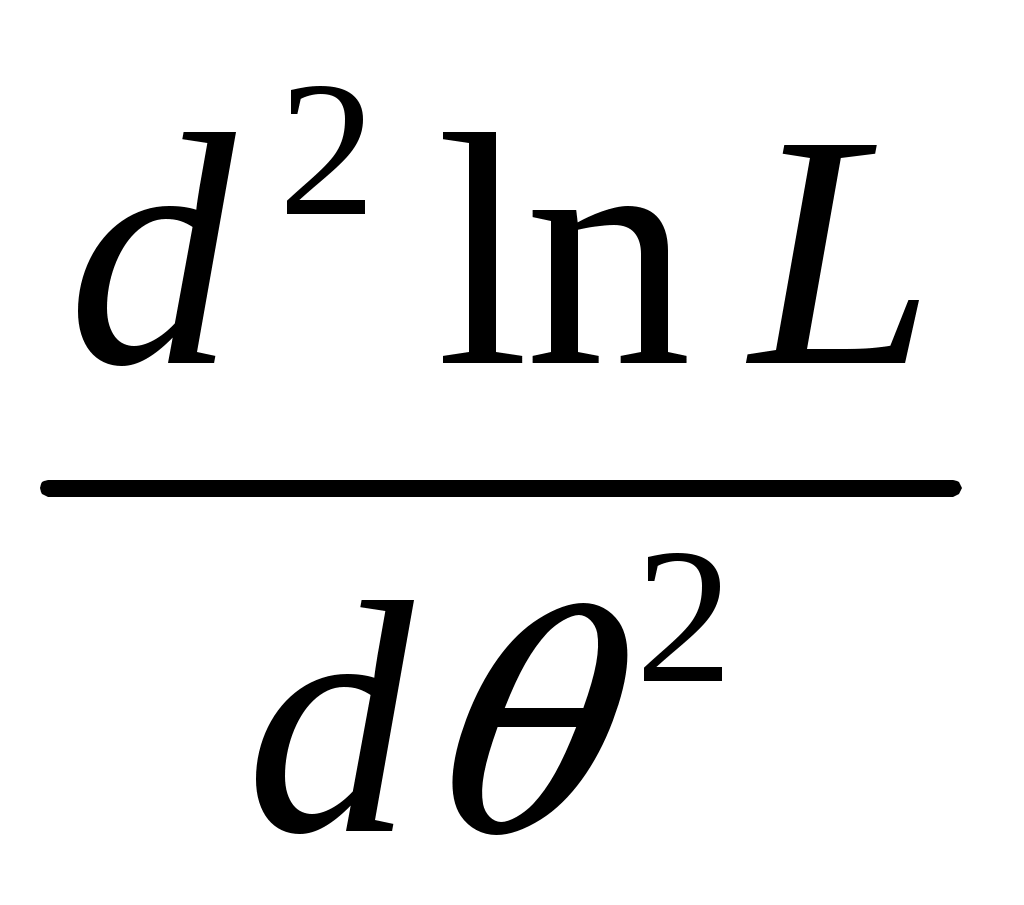; если вторая производная при

θ = θ* отрицательна, то θ* – точка максимума.

Найденную точку максимума θ* принимают в качестве оценки наибольшего правдоподобия параметра θ.

Б. Непрерывные случайные величины. Пусть X– непрерывная случайная величина, которая в результате п испытаний приняла значения х₁, х₂,..., х_п. Допустим, что вид плотности распределе­ния – функции f(x) – задан, но неизвестен параметр θ, которым оп­ределяется эта функция.

Функцией правдоподобия непрерывной случайной величины Xназы-вают функцию аргумента θ: L(x₁, x₂, ..., x_n; θ) = f(x₁; θ) ∙ f(x₂; θ) ∙ ... ∙ f(x_n; θ).

Оценку наибольшего правдоподобия неизвестного параметра распре-

деления непрерывной случайной величины ищут так же, как в случае дис-кретной случайной величины.

Если плотность распределения f(х)непрерывной случайной величины определяется двумя неизвестными параметрами θ₁ и θ₂, то функция правдоподобия есть функция двух независимых аргумен­тов θ₁ и θ ₂:

L= f(x₁; θ₁, θ ₂) ∙ f(x₂; θ ₁, θ ₂) ∙ ... ∙ f(x_n; θ₁, θ ₂).

Далее находят логарифмическую функцию правдоподобия и для отыскания ее максимума составляют и решают систему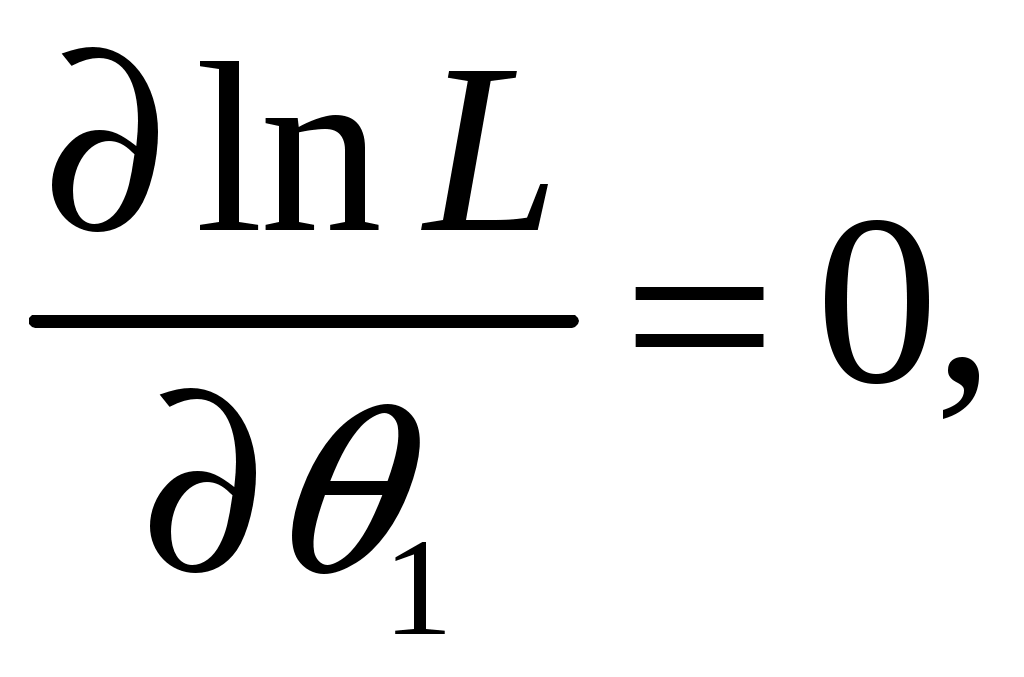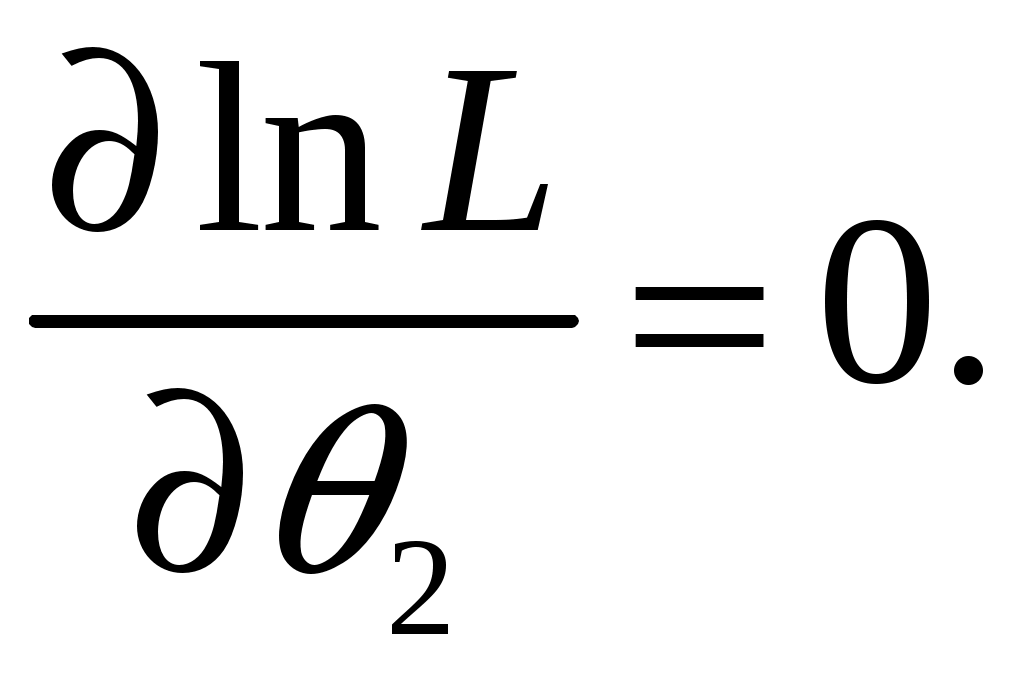





При малом числе наблюдений точечные оценки могут приводить к грубым ошибкам. Чтобы избежать этих ошибок, используют интервальные оценки.

Интервальной оценкой называют оценку, которая определяется дву-

мя числами и – концами интервала, накрывающего оцениваемый параметр . Пусть найденная по результатам выборки объема n статистическая характеристика является точечной оценкой неизвестного параметра . Чем меньше разность , тем лучше качество оценки, тем она точнее. Таким образом, положительное число  характеризует точность оценки

(2.10)

Однако статистический метод не позволяет категорически утверждать, что оценка удовлетворяет неравенству (2.10) в смысле математического анализа. Можно только говорить о вероятности (1–), с которой это неравенство выполняется.

Доверительной вероятностью оценки называют вероятность (1–) выполнения неравенства Обычно доверительная вероятность оценки задается заранее. Наиболее часто полагают (1–) = 0,95; 0,99; 0,9973. Доверительная вероятность точечной оценки показывает, что при извлечении выборки объема n из одной и той же генеральной совокупнос-ти в (1–) 100% случаях параметр  будет накрываться данным интервалом.

Пусть вероятность того, что равна (1–):



(2.11)

Формула показывает, что доверительный интервал накры-

вает неизвестный параметр  с заданной надежностью (1–). Чем меньше длина доверительного интервала , тем точнее оценка.

Длина доверительного интервала 2 определяется двумя величинами: доверительной вероятностью (1–) и объемом выборки n. Таким образом, , (1–) и n тесно взаимосвязаны и, задавая определенные значения двум из них, можно определить величину третьей. Например, пусть

Тогда,

1. Если  известно, то доверительный интервал, накрывающий неизвестное математическое ожидание a с заданной доверительной вероятностью (1–), имеет следующий вид: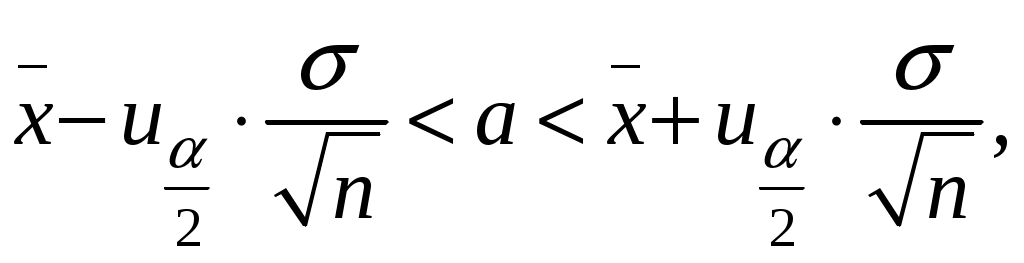



где 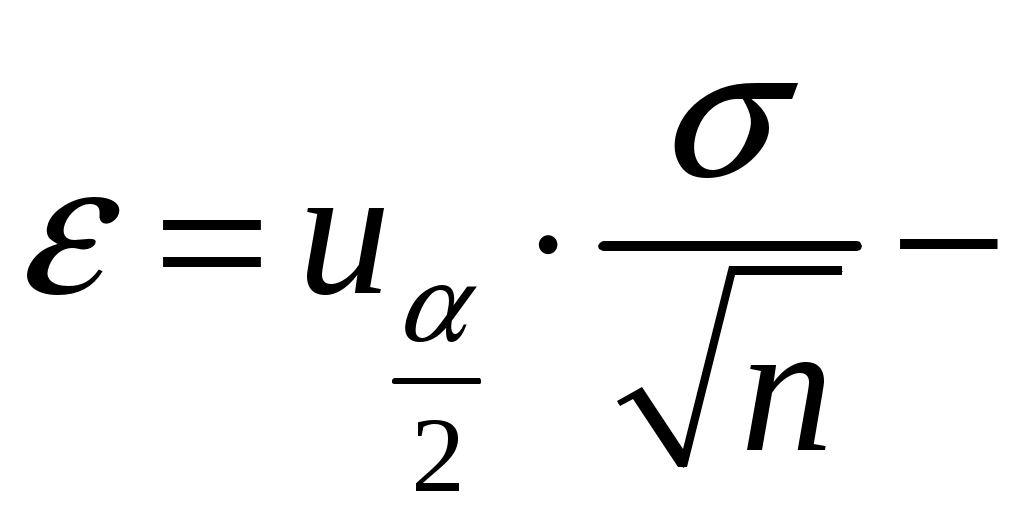– средняя арифметическая результатов измерений;n – объем выборки; квантиль нормированного нормального распределения, определяемый по доверительной вероятности (1–) из Приложения 2; точность (предельная погрешность) точечной оценки математического ожидания.

2. Если же  неизвестно, тогда доверительный интервал, накрывающий неизвестное математическое ожидание а СВ ХN (a,), имеет сле-дующий вид: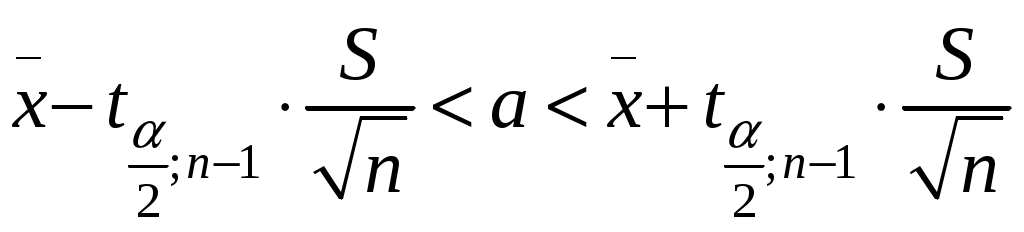

,

где 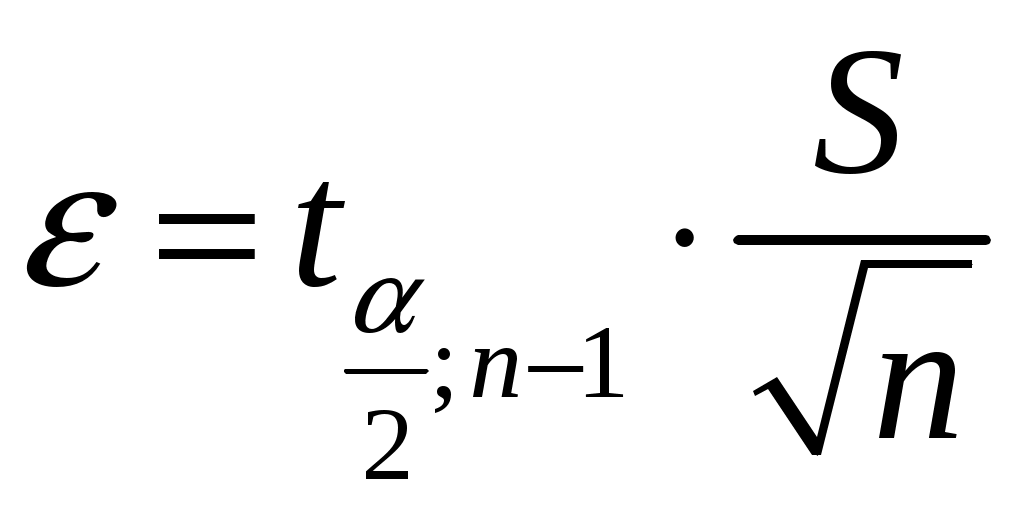– квантиль распределения Стьюдента, определяемый из Приложения 4 по заданной доверительной вероятности =1– и числу степеней свободы  =n–1 (n– объем выборки); – точечные несмещенные оценки параметров нормального распределения; – предельная погрешность точечного оценивания математического ожидания a.

3. Доверительный интервал для среднего квадратического отклонения  задается системой неравенств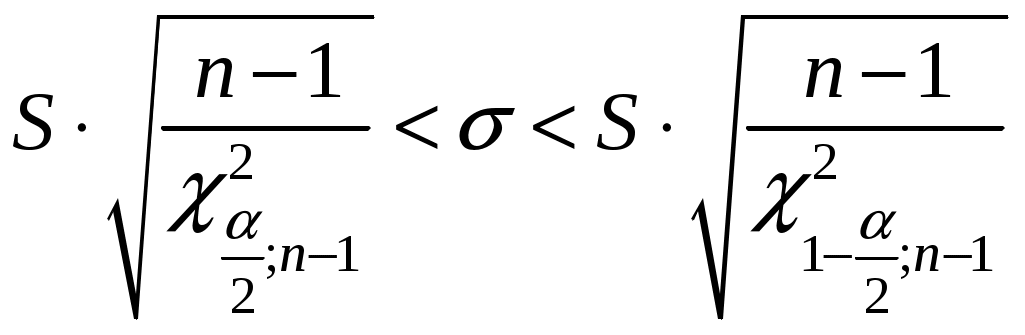

,

где ; – квантили ² распределения, определенные по таблице

распределения ² (Приложение 3) по заданной доверительной вероятности

(1–) и числу степеней свободы  = n–1.

Раздел 8. Статистическая проверка гипотез

Статистическая гипотеза (или просто гипотезой) – всякое высказывание (предположение) о генеральной совокупности, проверяемое по выборке.

Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотезы.

Различают два вида критериев: параметрические и непараметричес-кие. Предположение, которое касается неизвестного значения параметра распределения, входящего в некоторое параметрическое семейство распределений, называется параметрической гипотезой. Предположение, при котором вид распределения неизвестен (т.е. не предполагается, что оно входит в некоторое параметрическое семейство распределений), называется непараметрической гипотезой.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки.

Одну из гипотез выделяют в качестве основной (или нулевой) и обозначают , а другую, являющуюся логическим отрицанием , т.е. про-

тивоположную – в качестве конкурирующей (или альтернативной) ги-

потезы и обозначают

Гипотезу, однозначно фиксирующую распределения наблюдений, на-

зывают простой (в ней идет речь об одном значении параметра), в противном случае – сложной.

Правило, по которому принимается решение принять или отклонить

гипотезу (соответственно, отклонить или принять ), называется статистическим критерием (или просто критерием) проверки гипотезы Проверку гипотез осуществляют на основании результатов выборки , из которых формируют функцию выборки называемой статистикой критерия.

Основной принцип проверки гипотез состоит в следующем. Множество возможных значений статистики критерия разбивается на два непересекающихся подмножества: критическую область , т.е. область отклонения гипотезы и область принятия этой гипотезы. Если фактически наблюдаемое значение статистики критерия (т.е. значение критерия, вычисленное по выборке: ) попадает в критическую область , то основная гипотеза отклоняется и принимается альтернативная гипотеза если же попадает в то принимается а отклоняется. При проверке гипотезы может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов:

• ошибка I-го рода состоит в том, что отвергается нулевая гипотеза

когда на самом деле она верна;

• ошибка ІІ-го рода состоит в том, что отвергается альтернативная гипотеза когда она на самом деле верна.

Вероятность ошибки 1-го рода (обозначается через ) называется уровнем значимости критерия. Очевидно, . Чем меньше тем меньше вероятность отклонить верную гипотезу. Допустимую ошибку 1-го рода обычно задают заранее. В одних случаях считается возможным пренебречь событиями, вероятность которых меньше ( означает, что в среднем в 5 случаях из 100 испытаний верная гипотеза будет отвергнута), в других случаях, когда речь идет, например, о разрушении сооружений, гибели судна и т.п., нельзя пренебречь обстоятельствами, которые могут появиться с вероятностью, равной 0,001. Обычно для используются стандартные значения:

Вероятность ошибки 2-го рода обозначается через :  Величину ( ), т.е. вероятность недопущения ошибки 2-го рода (отвергнуть неверную гипотезу принятую верную ), называется мощностью критерия.

Очевидно, . Чем больше мощность критерия, тем вероятность ошибки 2-го рода меньше, что, конечно, желательно (как и уменьшение ).

Отметим, что одновременное уменьшение ошибок 1-го и 2-го рода возможно лишь при увеличении объема выборок. Поэтому обычно при заданном уровне значимости отыскивается критерий с наибольшей мощностью.

Методика проверки гипотез сводится к следующему:

1. Располагая выборкой формируют нулевую гипотезу и альтернативную

2. 
   В каждом конкретном случае подбирают статистику критерия обычно, из перечисленных ниже:
   

нормальное распределение, распределение хи-квадрата Пирсона, распределение Стьюдента, распределение Фишера-Снедекора.

2. 
   По статистике критерия K и уровню значимости определяют критическую область (и ) в зависимости от вида нулевой и альтернативной гипотез, формы и распределения критерия K. Для ее отыскания достаточно найти критическую точку т.е. границу (или квантиль), отделяющую область от
   

Границы областей определяются из соотношений:

• для правосторонней критической области

• для левосторонней критической области

• для двусторонней критической области S.

Для каждого критерия имеются соответствующие таблицы, по кото-

рым и находят критическую точку, удовлетворяющую приведенным выше

соотношениям.