Машфак. ТВ иМС для МСФ. Исследование связи между показателями, часть из которых являются случайными

• Название: Исследование связи между показателями, часть из которых являются случайными
• Анкор: Машфак
• Дата: 18.11.2022
• Размер: 2.07 Mb.
• Имя файла: ТВ иМС для МСФ.doc
• Тип: Исследование; #795733
• страница: 6 из 11

Пример 3.10. Дана матрица Р цепи Маркова с тремя состояниями

Найти р₃₂(3).

Решение. Согласно (2.2) имеем: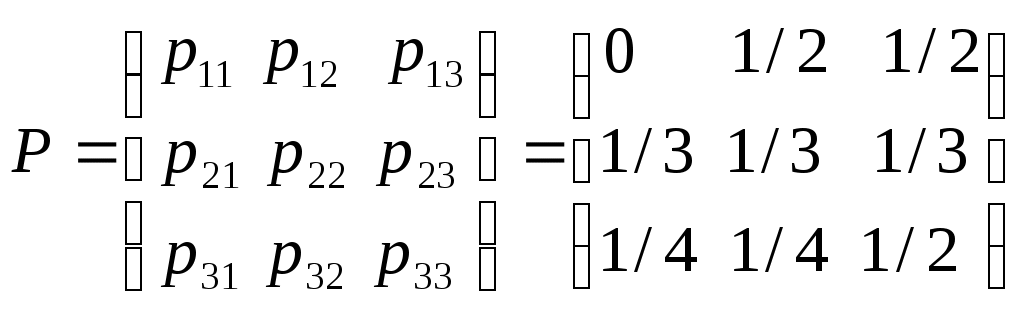

р₃₂(3) = р₃₁ р₁₂(2) + р₃₂ р₂₂(2) + р₃₃ р₃₂(2).

Необходимые вероятности перехода за 2 шага вычисляются следую-щим образом:

р₁₂(2) = р₁₁ р₁₂ + р₁₂ р₂₂ + р₁₃ р₃₂ = 7/24

р₂₂(2) = р₁₁ р₁₂ + р₂₂ р₂₂ + р₂₃ р₃₂= 13/36,

р₃₂(2) = р₃₁ р₁₂ + р₃₂ р₂₂ + р₃₃ р₃₂ = 1/3.

Отсюда р₃₂(3) = 95/288.

Соотношение (2.1) для всех i =1,...,n; j = 1,...,nможно представить

как произведение матриц: P(m) =p(l) p(m–l).

Пример 3.11. Для матрицы Р цепи Маркова с тремя состояниями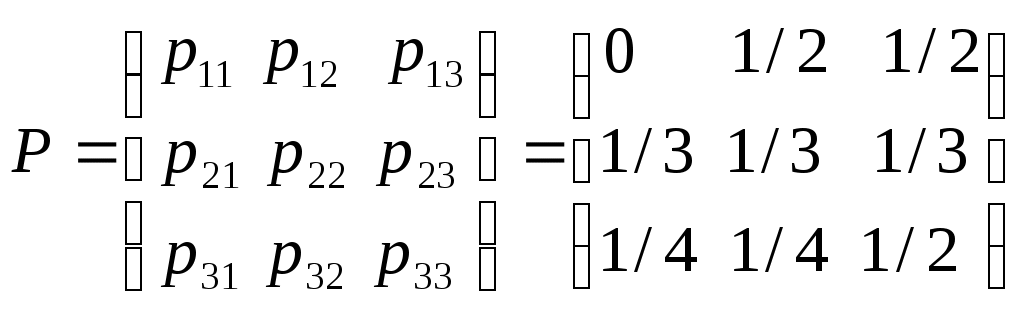

и вектора найти вероятность q₂(2).

Решение.. Согласно (2.5) имеем:

q₂(2) = q₁p₁₂(2) + q₂p₂₂(2) + q₃ р₃₂(2)=49/144.

Пример 3.12. Для многих экономических задач необходимо знать чередование годов с определенными значениями годовых стоков рек. Ко-нечно, это чередование не может быть определено абсолютно точно. Для определения вероятностей чередования (перехода) разделим стоки, введя четыре градации (состояния системы): первую (самый низкий сток), вто-рую, третью, четвертую (самый высокий сток). Будем для определенности считать, что за первой градацией никогда не следует четвертая, а за четвертой – первая из-за накопления влаги (в земле, водохранилищах и т.д.). Наблюдения показали, что в некоторой области остальные переходы возможны и:

а) из первой градации можно попасть в каждую из средних вдвое

чаще, чем опять в первую, т.е. р₁₁ =0,2; p₁₂ =0,4; p₁₃ =0,4; p₁₄ =0;

б) из четвертой градации переходы во вторую и третью градации бывают в 4 и 5 раз чаще, чем возвращение в четвертую, т.е. p₄₁=0; p₄₂=0,4; p₄₃=0,5; p₄₄=0,1;

в) из второй градации переход в другие градации может быть только реже: в первую – в два раза, в третью – на 25%, в четвертую – в четыре раза, чем переход во вторую, т.е. р₂₁ = 0,2; р₂₂ = 0,4; р₂₃ = 0,3; р₂₄ = 0,1;

г) из третьей градации переход во вторую градацию столь же вероя-

тен, как и возвращение в третью градацию, а переходы в первую и четвер-

тую градации бывают в четыре раза реже, т.е. р₃₁ = 0,1; р₃₂ = 0,4;

р₃₃ = 0,4; р₃₄ = 0,1;

Решение. Построим граф состояний данной цепи Маркова и разметим его переходными вероятностями (рис. 3.4):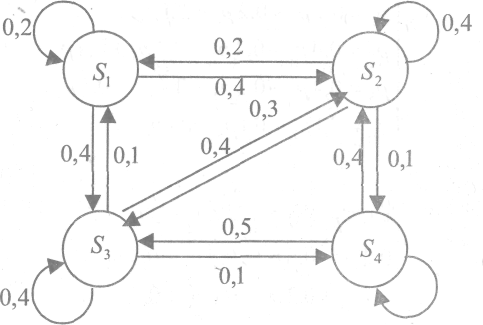



Рис. 3.4. Граф состояний цепи Маркова

Составим матрицу вероятностей перехода:

0,2 0,4 0,4 0

Р= 0,2 0,4 0,3 0,1

0,1 0,4 0,4 0,1

0 0,4 0,5 0,1 .

Найдем среднее время между засухами и полноводными годами для стоков рек. Для этого нужно найти предельное распределение. Ясно, что за два шага можно перейти из любого состояния данной системы в любое другое, так как матрица Р(2) не содержит нулевых элементов.

Н айдем предельные вероятности, исходя из условия: p=pP. Запишем это условие в виде системы:

p₁= p₁p₁₁ + p₂p₂₁ +p₃p₃₁ +p₄p₄₁,

p₂= p₁p₁₂ + p₂p₂₂ +p₃p₃₂ +p₄p₄₂,

p₃= p₁p₁₃ + p₂p₂₃ +p₃p₃₃ +p₄p₄₃,

p₄= p₁p₁₄ + p₂p₂₄ +p₃p₃₄ +p₄p₄₄.

Таким образом,

p₁= 0,2p₁ + 0,2p₂ +0,1p₃,

p₂= 0,4 p₁ + 0,4 p₂ +0,4 p₃ +0,4 p₄,

p₃= 0,4 p₁ + 0,3 p₂ +0,4 p₃ +0,5 p₄,

p₄= 0,1 p₂ + 0,1 p₃ +0,1 p₄

или

-0,8 p₁ + 0,2 p₂ + 0,1 p₃ =0,

0,4 p₁ - 0,6 p₂+ 0,4 p₃ +0,4 p₄ = 0,

0,4 p₁ + 0,3 p₂ - 0,6 p₃ +0,5 p₄ = 0,

0,1 p₂ + 0,1 p₃ - 0,9 p₄ = 0.

Это однородная система линейных алгебраических уравнений. Ее можно решить, например, методом Гаусса:
0,4p₁ - 0,6 p₂ + 0,4p₃ +0,4p₄ = 0,

0,1 p₂ + 0,1 p₃ - 0,9p₄ = 0,

-1,9p₃ + 8,2 p₄ = 0.

Система приведена к треугольному виду. Имеем три уравнения и четыре неизвестных, поэтому добавим условие p₁+р₂+ р₃+р₄= 1, так как система с вероятностью 1 находится в одном из своих состояний.

Тогда имеем:

p₁ = (1/4) (6p₂ – 4p₃ – 4p₄), p₁ = 65/38p₄,

p₂ = 9p₄ – p₃, или p₂ = 89/19p₄,

p₃ = 82/19p₄, p₃= 82/19 p₄,

p₁+p₂+p₃+p₄=1. 65/38p₄+89/19p₄+82/19p₄+p₄=1.

Следовательно, p₄= 38/445; p₃=164/445; p₂=178/445; p₁=65/445.

Периодичность возвращения в состояние S_i равна 1/p_i, а предельные

вероятности засушливых и дождливых лет соответственно равны

p₁ = 65/445» 0,15 и p₄ = 38/445 » 0,08. Следовательно, периодичность засушливых лет в среднем равна 6-7 лет, а дождливых – 12-13 лет.
3.2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Пример 3.9. Дана выборка:

2	4	2	4	3	3	3	2	0	6	1	2	3	2	2	4	3	3	5	1
0	2	4	3	2	2	3	3	1	3	3	3	1	1	2	3	1	4	3	1
7	4	3	4	2	3	2	3	3	1	4	3	1	4	5	3	4	2	4	5
3	6	4	1	3	2	4	1	3	1	0	0	4	6	4	7	4	1	3

Требуется:

1. 
   составить дискретный вариационный ряд;
   
2. 
   построить график дискретного вариационного ряда (полигон);
   
3. 
   составить эмпирическую функцию распределения;
   
4. 
   построить график эмпирической функции распределения;
   
5. 
   вычислить числовые характеристики дискретного вариационного ряда:
   

- выборочное среднее арифметическое ;

- выборочная дисперсия ;

- выборочное среднее квадратичное отклонение ;

- выборочная мода;

- выборочная медиана.

Решение. Составим таблицу, в первом столбце которой указаны ва-рианты, во втором – частоты, в третьем – относительные частоты (частос-ти), в четвертом – накопленные относительные частоты, как сумма относительных частот.

Варианта	Частота	Относительная частота	Накопленная относительная частота
0	4	0,0506	0
1	13	0,1646	0,0506
2	14	0,1772	0,2152
3	24	0,3038	0,3924
4	16	0,2025	0,6962
5	3	0,0380	0,8987
6	3	0.0380	0,9367
7	2	0,0253	0,9747
	79	1,0000	1,0000

Первый и второй, первый и третий столбцы таблицы определяют соответственно дискретный вариационный ряд частот и относительных частот.

При построении полигона относительных частот (рис. 3.5) на оси аб-цисс откладываем значения вариант, а на оси ординат– относительные частоты.

Эмпирическую функцию распределения 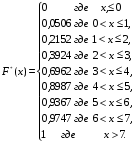находим, используя накопленные относительные частоты:



При построении графика откладываем на оси абсцисс значения вариант, а на оси ординат – значения эмпирической функции распре-деления (рис. 3.6).

Выборочные среднюю и дисперсию найдём по формулам (4) и (5):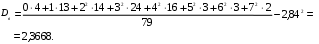

;



Выборочное среднее квадратичное отклонение: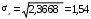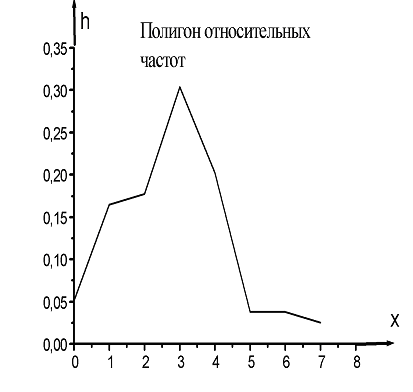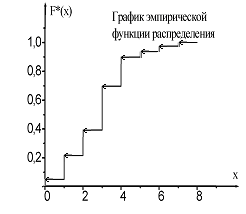





Рис. 3.5 Рис. 3.6
Выборочной модой является значение с максимальной частотой, т.е. .

Выборочной медианой служит 40-е значение вариационного ряда:

.

Пример 3.10. Найти с надёжностью доверительный интер-вал для неизвестного математического ожидания m нормально распреде-лённого признака Х генеральной совокупности, если генеральное среднее квадратичное отклонение выборочная средняя и объём выборки