Машфак. ТВ иМС для МСФ. Исследование связи между показателями, часть из которых являются случайными
 Скачать 2.07 Mb. Скачать 2.07 Mb.
|
|
Задание 4 В городе имеются Nоптовых баз. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна p. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент.
Задание 5 Непрерывная случайная величина X задана интегральной функцией распределения найти дифференциальную функцию распределения найти математическое ожидание построить графики интегральной и дифференциальной функций распределения. 1. 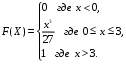 2. 2. 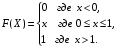 3. 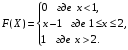 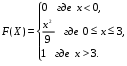 5. 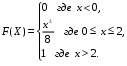 6. 6. 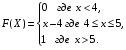 7. 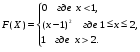 8. 8.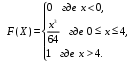 9. 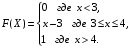 10. 10. 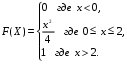 11. 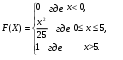 12. 12. 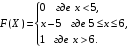 13. 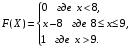 14. 14. 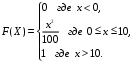 15. 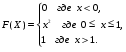 16. 16. 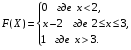 17. 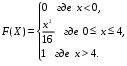 18. 18. 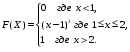 19. 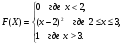 20. 20. 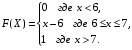 21. 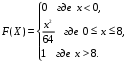 22. 22. 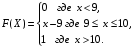 23. 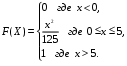 24. 24. 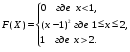 25. 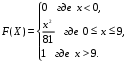 26. 26. 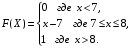 27. 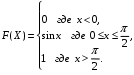 28. 28. 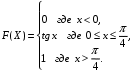 29.  30 . 30 . Задание 6 Непрерывная случайная величина имеет нормальное распределение. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (a,b).
Задание 7 Автомашина может находиться в одном из четырех состояний: – исправна; – неисправна, осматривается; – ремонтируется; – списана. Если машина исправна, то с вероятностью p1 она может сломаться; если машина неисправна, то она с вероятностью p2 ремонтируется или с вероятностью p3 списывается; если же машина ремонтируется, то она с вероятностью p4 становится исправной, либо с вероятностью p5 продолжает ремонтироваться. Остальные переходы считать невозможными. Найти вероятность того, что машина будет исправна в субботу, если известно, что она была исправна в среду. Найти предельные вероятности системы, состоящие из 4-х состояний.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
