Машфак. ТВ иМС для МСФ. Исследование связи между показателями, часть из которых являются случайными

• Название: Исследование связи между показателями, часть из которых являются случайными
• Анкор: Машфак
• Дата: 18.11.2022
• Размер: 2.07 Mb.
• Имя файла: ТВ иМС для МСФ.doc
• Тип: Исследование; #795733
• страница: 2 из 11

2.2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Раздел 6. Эмпирические характеристики выборки

Основными понятиями математической статистики являются гене-ральная совокупность, выборка, эмпирическая функция распределения.

Генеральная совокупность – множество всех мыслимых значений наблюдений (объектов), однородных относительно некоторого признака. Число всех наблюдений, составляющих генеральную совокупность, называется ее объемом и обозначается N.

Выборка – совокупность случайно отобранных наблюдений (объектов). Объем выборки n (n<< N).

Операция, заключенная в расположении значений признака Х по возрастанию, называется ранжированием опытных данных. Значение которое принимает признак, называется вариантой. Число элементов в каждой группе называется частотой варианта Число наблюдений варианты m_i называется частотой встречаемости.

Отношения частот к объему выборки называются относительными частотами (частностями) вариант: _i = m_i/n.

Накопленная (кумулятивная) частота показывает, сколько наблюдалось элементов выборки со значениями признака, меньшими x_i. Отношение накопленной частоты к общему объему выборки, т.е. называется относительной накопленной частотой.

Совокупность вариант х_i и соответствующих им частот m_i и (или) относительных частот называется статистическим распределением вы-борки.

Последовательность вариант, записанных в возрастающем порядке,

называется вариационным рядом.

Дискретным вариационным рядом называется ранжированная последовательность вариантов с соответствующими частотами.

Для наглядного представления статистического распределения пользуются графическим изображением вариационных рядов: полигоном и гистограммой.

Полигон частот (частностей) – ломаная, отрезки которой соединяют точки (х_i,m_i) [ ].

Гистограмма относительных частот (или просто гистограмма)– сту-

пенчатая фигура, состоящая из смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине h, а вы-

соты равны . Ширину интервала hможно определить по формуле

Стерджесса: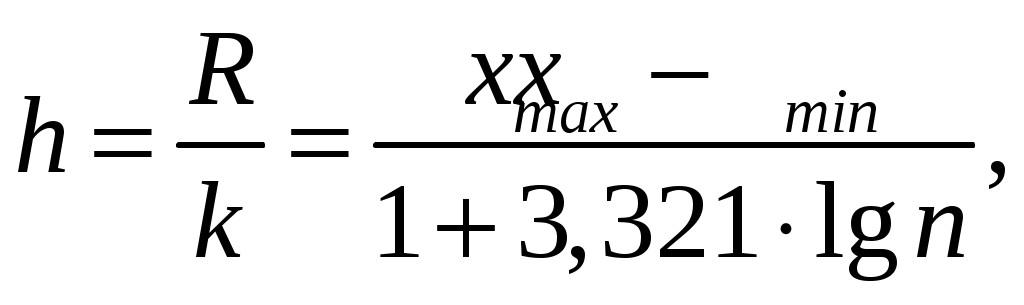



где х_mах – максимальное, х_min – минимальное значения вариант, n – объем выборки, R– размах варьирования, k – число интервалов ( ).

Гистограмма является аналогом дифференциальной функции случайной величины.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения х относительную частоту события :



где – число вариант, меньших х; – объём выборки.

Свойства функции :

1^о.

2^о. – неубывающая функция.

3^о.

4^о. непрерывна слева.

5^о. = 0 при = 1 при

Функция является "ступенчатой", имеются разрывы в точках, которым соответствуют наблюдаемые значения вариантов. Величина скач- ка равна относительной частоте варианта.

Аналитически 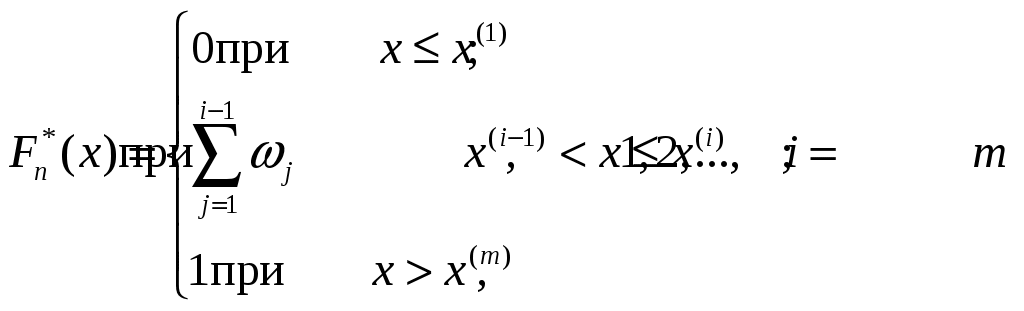задается следующим соотношением:



где

– соответствующие относительные частоты;

– элементы вариационного ряда (варианты).

Выборочной средней называется величина

= . (2.6)

Средняя арифметическая имеет те же единицы измерения, что и вари-

анты.

Свойства средней арифметической:

1° cредняя арифметическая постоянной равно самой постоянной:



2º сумма отклонений результатов наблюдений от их средней арифметической равна нулю: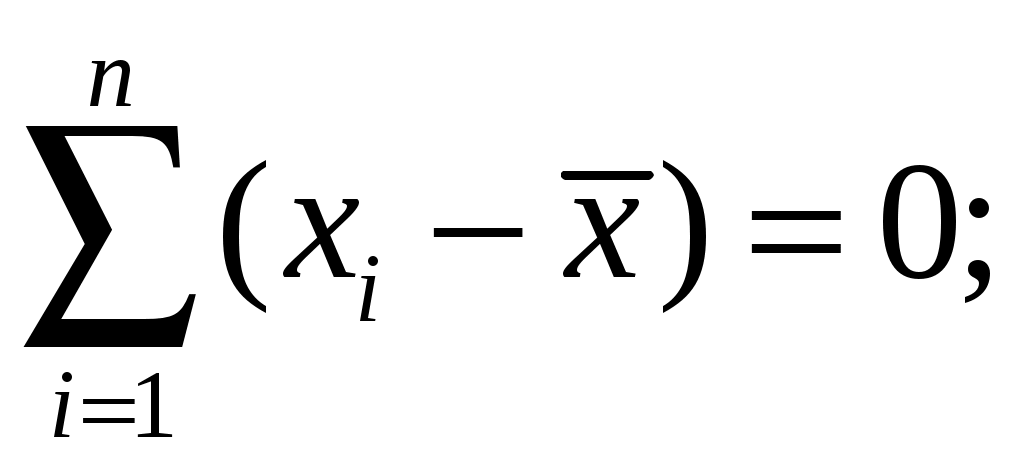

3º если все результаты наблюдений умножить на одно и то же число С, то имеет место равенство т.е. постоянную С можно выносить за знак средней арифметической;

4º если все результаты наблюдений увеличить (уменьшить) на одно

и то же число С, то средняя арифметическая увеличится (уменьшится) на то же число: =

5º если все частоты вариантов умножить на одно и то же число, то средняя арифметическая не изменится;

6º средняя арифметическая алгебраической суммы соответствующих друг другу значений, принадлежащих двум группам наблюдений, равна алгебраической сумме средних арифметических этих групп:

7º если ряд наблюдений состоит из двух непересекающихся групп наблюдений, то средняя арифметическая 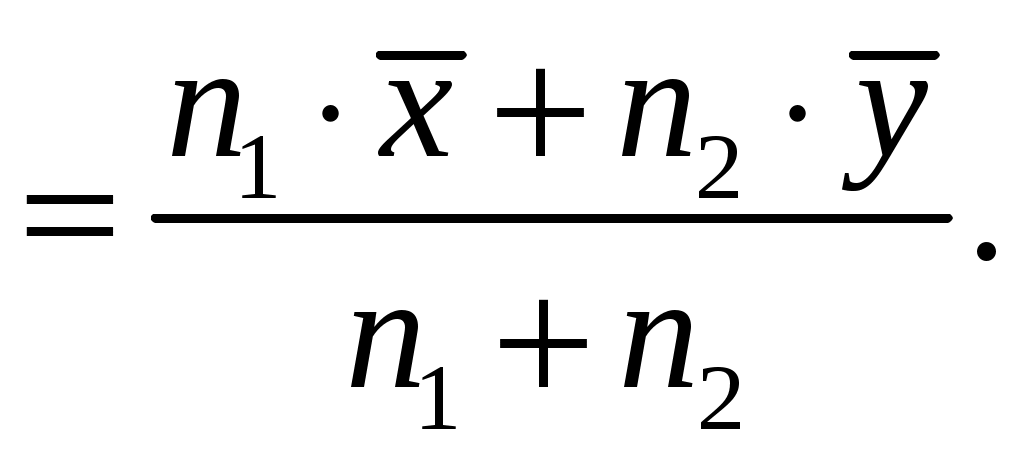всего ряда наблюдений равна взвешенной средней арифметической групповых средних и , причем весами являются объемы групп и соответственно:



Математическое ожидание (Х) дискретной случайной величины Х является постоянной величиной в отличие от которая не обладает этим свойством. Несмотря на принципиальные различия, (Х) и имеют между собой много общего (в частности, они обладают одинаковыми свойствами) и поэтому естественно считать последнюю выборочным аналогом математического ожидания.

Для изучения степени изменчивости признака вводят показатели вариации:

размах вариации (варьирования) R= x_max – x_min;

выборочная дисперсия 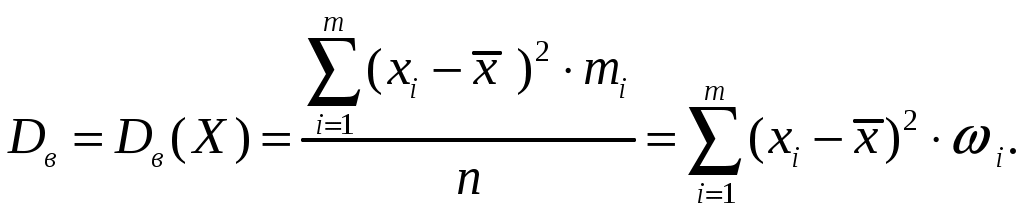(2.7)

Можно показать справедливость следующих выражений, являющихся аналогами формулы (2.7) соответственно: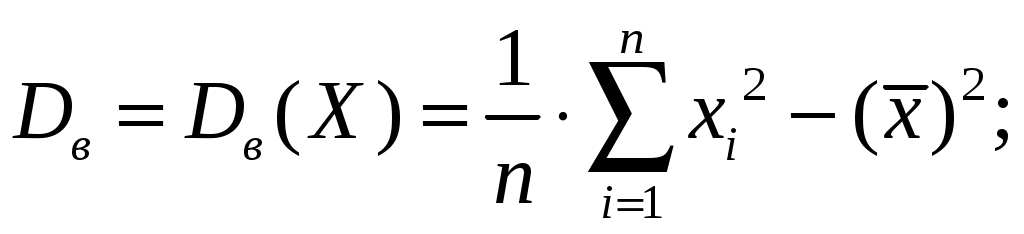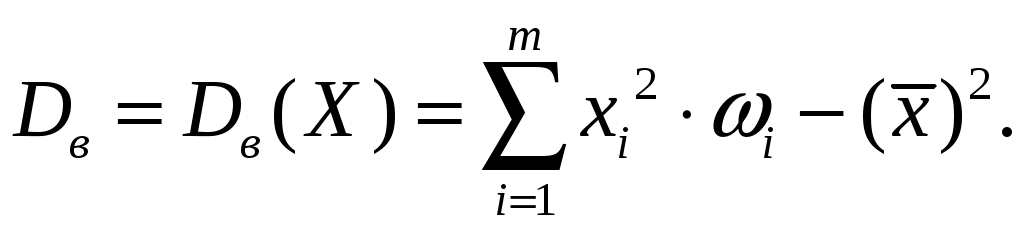





Коэффициент вариации cv – это отношение среднего квадратичного

отклонения к средней величине признака, выраженное в процентах:

Cv = .

Если выборка мала (n 30), то используют выборочную исправленную дисперсию: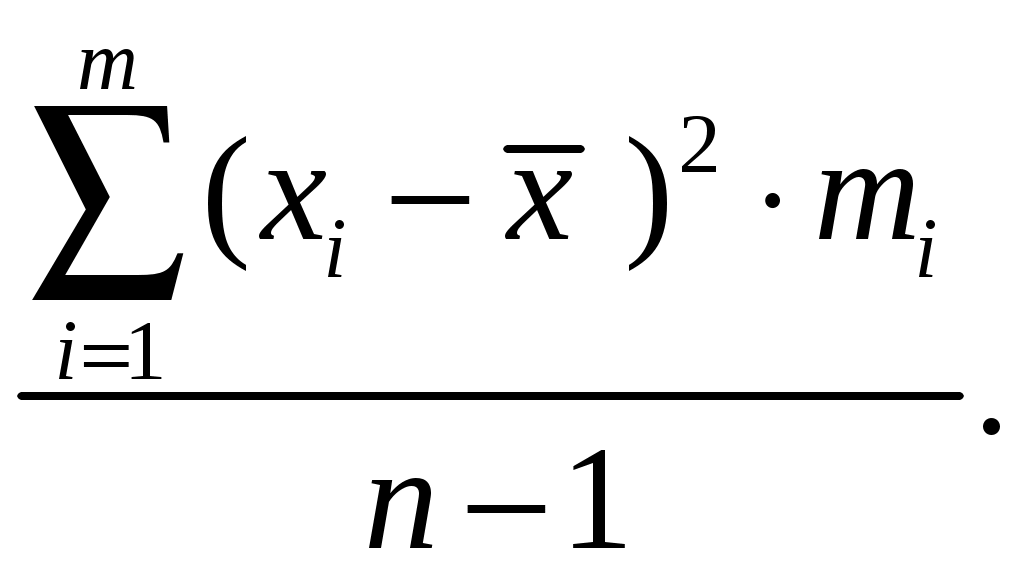

(2.8)

Замечание. В случае интервального вариационного ряда под понимается середина i-го частичного интервала.

Выборочное среднее квадратичное отклонение или (2.9)

Свойства выборочной дисперсии:

1° дисперсия постоянной величины равна нулю:

2º если все результаты наблюдений увеличить (уменьшить) на одно и то же число С, то дисперсия и среднее квадратическое отклонение не изменятся:

3° дисперсия равна средней арифметической из квадратов значений признака минус квадрат средней арифметической:

4° если все результаты наблюдений умножить на одно и то же число С, то имеют место равенства:

5^о если все частоты вариантов умножить на одно и то же число, то

дисперсия и среднее квадратическое отклонение не изменятся.

Моменты распределения представляют собой систему числовых характеристик, с помощью которых можно описать все особенности вариации признака (среднюю тенденцию, рассеяние, форму распределения и т.д.).

Эмпирическим начальным моментом 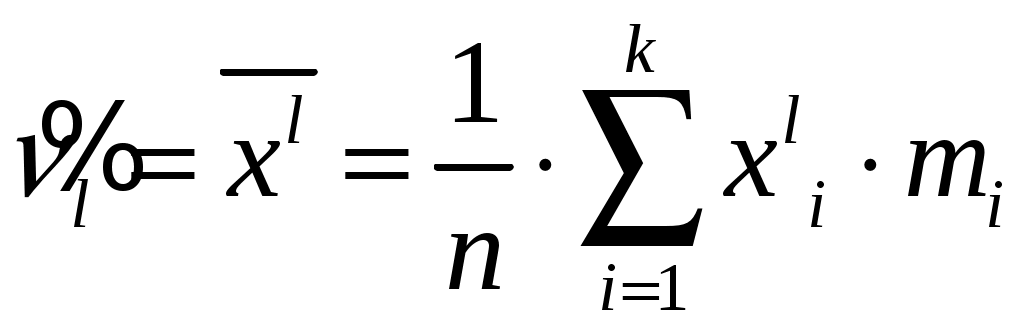порядка l называют взвешенную среднюю арифметическую l-х степеней вариантов:

;

и т.д.

Эмпирическим центральным моментом порядка называют взвешенную среднюю арифметическую l-x степеней отклонений вариантов от их средней:

;

; ; и т.д.

Эмпирический центральный момент 3-го порядка используется при

построении показателя асимметрии распределения

Если в вариационном ряду то большую частоту имеют варианты, меньшие, чем такой ряд является отрицательно асимметричным.

Эмпирический эксцесс характеризует крутизну распределе-

ния.

Раздел 7. Точечные и интервальные оценки

Числовые значения, характеризующие генеральную совокупность, на-зываются параметрами. Одна из задач математической статистики – опре-деление параметров большого массива по исследованию его части.

Статистическое оценивание может выполняться двумя способами:

1) точечная оценка – оценка, которая дается для некоторой опреде-ленной точки;

2) интервальная оценка – по данным выборки оценивается интервал, который покрывает истинное значение с заданной вероятностью.

Точечная оценка – это выборочная характеристика, определяемая од-

ним числом и используемая в качестве приближенного значения неизвест-ной характеристики генеральной совокупности. Так, статистической оценкой плотности распределения непрерывной случайной величины является гистограмма.

Качество оценки устанавливается по трем свойствам: быть состоя-тельной, эффективной и несмещенной.

Точечная оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру при любом объеме выборки.

Точечная оценка называется состоятельной, если при увеличении объема выборки выборочная характеристика стремится к соответствующей характеристике генеральной совокупности.

Несмещенная точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками.

Несмещенной оценкой генеральной средней (математического ожи-дания) является выборочная средняя , а генеральной дисперсии – ис-правленная выборочная дисперсия.

Интервальная оценка – числовой интервал, который определяется дву-мя числами – границами интервала, покрывающий неизвестный параметр генеральной совокупности.

Доверительный интервал – интервал, в котором с той или иной зара-нее заданной вероятностью находится неизвестный параметр генеральной совокупности.

Доверительная вероятность  – такая вероятность, что событие ве-роятности 1– можно считать невозможным; = 1– – это уровень значи-мости.

Пусть СВ Х имеет, например, нормальное распределение ХN(a,), где параметры а и  неизвестны. С целью их определения производится эксперимент, в результате которого фиксируется n значений случайной величины Х: х₁, х₂, ... , х_n. Результаты измерения х₁, х₂, ... , х_n рассматривают как выборку объема n из бесконечной генеральной совокупности. На основании этой выборки необходимо «оценить» (найти приближенные значения) двух параметров – математического ожидания а и среднего квадратического отклонения . Вообще говоря, по результатам выборки, какого бы большого размера она ни была, нельзя определить точные значения неизвестных параметров а и , но можно найти их приближенные значения , которые называются оценками.

Для нахождения приближенных значений неизвестных параметров а и  нормального закона будем рассматривать функции вида:

и

которые называются выборочными функциями или статистиками.

Задача оценки неизвестных параметров а и  сводится к нахождению таких статистик и которые могут быть использованы для приближенного определения значений неизвестных параметров а и .

Можно показать, что если ХN(a,), то точечные оценки неизвестных параметров a и находятся по формулам (2.6) и (2.8). Эти оценки обладают свойствами несмещенности, состоятельности и эффективности.

Обозначим через неизвестную вероятность события в одном испытании. Для оценивания проведем n независимых испытаний, в которых событие произошло m раз. Тогда случайная величина



называется частностью (относительной частотой) события А, которая является состоятельной, несмещенной и эффективной оценкой вероятности .

В общем виде выборочное среднее является состоятельной ине-смещенной оценкой математического ожидания (генеральной средней ) генеральной совокупности

Выборочная дисперсия является состоятельной, но смещенной оценкой генеральной дисперсии D(X).

Исправленная дисперсия является состоятельной и несмещенной оценкой для генеральной дисперсии D(X).

Метод моментов точечной оценки неизвестных параметров заданно-го распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.

Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка. Например, можно прирав­нять начальный теоретический момент первого порядка к начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка к центральному эмпирическому моменту второго порядка:

v₁ = ,µ₂ =

Учитывая, что v₁ = М(X), 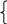= µ₂ = D(Х), = D_в, имеем:

М(X) =

D(Х) = D_в.

Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив систему относительно неизвестных параметров, тем самым получим их точечные оценки.

Метод наибольшего правдоподобия точечной оценки неизвестных параметров заданного распределения сводится к отысканию макси­мума

функции одного или нескольких оцениваемых параметров.