Машфак. ТВ иМС для МСФ. Исследование связи между показателями, часть из которых являются случайными
 Скачать 2.07 Mb. Скачать 2.07 Mb.
|
|
ББК 60.6я73 ВВЕДЕНИЕ Теория вероятностей – математическая наука, изучающая закономер-ности случайных явлений. Она изучает случайные события и случайные величины. Первые работы, в которых появились основные понятия теории ве-роятностей, представляли собой попытки создания теории азартных игр. Этот период относится к ХVI –XVII векам. Статистика возникла существенно раньше теории вероятностей. Еще в глубокой древности проводились переписи населения и велись земельные кадастры. На протяжении веков статистика искала свой математический аппарат и нашла его в теории вероятностей. В результате возник такой раздел математики, как математическая статистика, изучающая прибли-женные методы отыскания законов распределения и числовых харак-теристик по результатам эксперимента. В математической статистике принято выделять три основных на-правления исследований: - оценка параметров генеральной совокупности; - проверка статистических гипотез (некоторых априорных предпо-ложений); - исследование связи между показателями, часть из которых являют-ся случайными. Проведение экономических исследований, оценка хозяйственной дея-тельности предприятий, микро- и макроэкономических показателей, прог-ноз этих показателей на будущее невозможны без использования матема-тического аппарата теории вероятностей и математической статистики. Этот аппарат позволяет получать наиболее вероятные количественные зна-чения экономических показателей, обучать методам обработки и анализа результатов эксперимента и выработать навыки математического иссле-дования прикладных вопросов, устанавливать связь между различными случайными параметрами и принимать обоснованные решения в экономи-ке. Указания содержат рабочую программу, справочный материал, со-держащий минимум теоретических сведений в виде формул, свойств и алгоритмов, образцы решения типовых заданий, предлагаемых для выпол-нения аудиторных и домашних контрольных работ, рекомендуемую литературу. 1. РАБОЧАЯ ПРОГРАММА КУРСА (РАЗДЕЛА) «Теория вероятностей и математическая статистика» ЧАСТЬ 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Раздел 1. Предмет и задачи теории вероятностей. Области применения в экономике. Случайные величины. Вероятности событий 1.1. Основные понятия комбинаторики: комбинаторные правила сложения и умножения, перестановки, сочетания из n по m, размещения из n по m, сочетания с повторениями. 1.2. Случайные события, частота и вероятность. Классический способ подсчета вероятностей. Статистическое определение вероятности. Геометрические вероятности. Пространство элементарных событий. Случайное событие как подмножество в пространстве элементарных событий. 1.3. Алгебра событий. Аксиомы вероятности и вероятностное пространство. Следствия из аксиом. Основные формулы для вычисления вероятностей. Независимые события. Условные вероятности. Теорема умножения вероятностей. Формулы полной вероятности и Байеса вероятностей гипотез. 1.4. Схема повторных независимых испытаний (схема Бернулли). Формула Бернулли. Наиболее вероятное число успехов в схеме Бернулли. Приближенные формулы Лапласа. Функции Гаусса и Лапласа. Предельная теорема и приближенная формула Пуассона. Раздел 2. Случайные величины 2.1. Случайная величина как функция на пространстве элементарных событий. Функция и плотность распределения вероятностей случайной величины. Свойства функции и плотности распределения вероятностей случайных величин. Независимость случайных величин. 2.2. Функции от одной или нескольких случайных величин. Арифметические операции над случайными величинами. 2.3. Дискретная случайная величина (ДСВ) и ее закон распределения. Основные числовые характеристики ДСВ: математическое ожидание, дисперсия, стандартное отклонение, ковариация и коэффициент корреляции. Математическое ожидание функции от ДСВ. 2.4. Свойства математического ожидания и дисперсии. Примеры классических дискретных распределений (биномиальное, пуассоновское, геометрическое) и вычисление их числовых характеристик. Пуассоновость суммы независимых пуассоновских случайных величин. Непрерывные и абсолютно непрерывные случайные величины. Свойства функции плотности. Математическое ожидание и дисперсия непрерывной случайной величины. Математическое ожидание функции от абсолютно непрерывной случайной величины. 2.5. Равномерное распределение на отрезке, показательное (экспоненциальное) распределение, распределение Коши, нормальное и логнормальное распределения, их числовые характеристики. Нормальность суммы независимых нормальных случайных величин. Правило «трех сигм» в общем случае. Начальные и центральные моменты случайной величины. Асимметрия и эксцесс. Мода, медиана и квантили непрерывного распределения. Раздел 3. Случайные векторы 3.1. Совместное распределение случайных величин. Случайный вектор. Зависимые и независимые случайные векторы. Функция и плотность распределения случайного вектора и их свойства. Одинаково распределенные случайные векторы. Связь функции распределения случайного вектора с функциями распределения его компонент. 3.2. Дискретные случайные векторы. Вероятность попадания дискрет-ного случайного вектора в заданное множество. Закон распределения двумерного дискретного случайного вектора и его связь с распределениями компонент. 3.3. Абсолютно непрерывные случайные векторы. Вероятность попадания абсолютно непрерывного случайного вектора в заданное множество. Связь функции плотности распределения случайного вектора с функциями плотности его компонент. Функция плотности и независимость компонент случайного вектора. Равномерное распределение в ограниченной области в пространстве 3.4. Числовые характеристики дискретных и абсолютно непрерывных случайных векторов. Математическое ожидание функции от компонент случайного вектора. Ковариационная матрица случайного вектора. Неотрицательная определенность ковариационной матрицы. 3.5. Нормальное распределение в R2. Плотность двумерного нормаль-ного распределения, приведение к каноническому виду. Нормальные случайные векторы и их свойства. 3.6. Условные распределения и условные плотности. Условное математическое ожидание и его свойства. Формула полного математического ожидания. Условная дисперсия. Формула полной дисперсии. Ковариация и коэффициент корреляции. Раздел 4. Предельные теоремы теории вероятностей 4.1. Закон больших чисел. Неравенство Чебышева. Теоремы Чебышева и Бернулли. Последовательности случайных величин. Сходимость по вероятности. 4.2. Центральная предельная теорема (ЦПТ) в форме Ляпунова для одинаково распределенных слагаемых и в общем случае. Применение ЦПТ. Раздел 5. Цепи Маркова 5.1. Определение и способы задания цепей Маркова. Вероятности и матрица переходов. Многошаговые вероятности переходов и теорема о матрице многошаговых переходов. Предельные вероятности. Теорема Маркова о предельных вероятностях. Часть II. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА Раздел 6. Эмпирические характеристики и выборки 6.1. Основные задачи математической статистики. Генеральная совокупность. Вариационный ряд. Статистическое распределение выборки. По-лигон и гистограмма. Эмпирическая функция распределения и ее график. 6.2. Выборочные числовые характеристики: среднее, дисперсия, мода, медиана, моменты высших порядков (асимметрия, эксцесс). Раздел 7. Точечные и интервальные оценки 7.1. Статистические оценки параметров распределения. Несмещенно-сть, состоятельность и эффективность точечных оценок. Оценка неизвест-ной вероятности по частоте. Точечные оценки для математического ожидания и дисперсии. 7.2. Метод моментов. Метод максимального правдоподобия. 7.3. Доверительные вероятности и интервалы. Приближенные доверительные интервалы для оценки генерального среднего и дисперсии. Раздел 8. Статистическая проверка гипотез 8.1. Статистическая проверка гипотез. Параметрические и непараметрические гипотезы. Ошибки I и II рода. Уровень значимости и мощность критерия. Проверка гипотез о равенстве средних и дисперсий двух нормально распределенных генеральных совокупностей. Простые и сложные гипотезы. 8.2. Хи-квадрат критерий Пирсона. Проверка гипотезы о соответствии наблюдаемых значений предполагаемому распределению вероятностей (дискретному или непрерывному). Сравнение параметров двух нормальных распределений. Раздел 9. Дисперсионный анализ 9.1. Однофакторный дисперсионный анализ. Общая, факторная и остаточная суммы квадратов отклонений. Выборочные дисперсии. Сравнение нескольких средних методом дисперсионного анализа. 9.2. Понятие о двухфакторном дисперсионном анализе. Раздел 10. Корреляционно-регрессионный анализ (двумерная модель) 10.1. Функциональная, стохастическая и корреляционная зависимос-ти. Эмпирическая ковариация и коэффициент корреляции. 10.2. Основные положения регрессионного анализа. Парная линейная регрессионная модель. Предпосылки регрессионного анализа. Нелинейная регрессия. 2. СПРАВОЧНЫЙ МАТЕРИАЛ 2.1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ Раздел 1. Предмет и задачи теории вероятностей. Области применения в экономике. Случайные величины. Вероятности событий Комбинаторика есть теория конечных множеств, изучающая вопросы, связанные с количеством комбинаций, подчиненных тем или иным усло-виям, которые можно составить из заданного конечного множества объектов произвольной природы. Наиболее употребительны комбинации без повторений: перестановки, сочетания и размещения. Число всевозможных перестановок из n различных элементов равно Сочетаниями из n элементов по m в каждом называются такие ком-бинации, из которых каждая содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга, по крайней мере, одним элементом; общее число различных сочетаний определяется формулой  где где Размещениями из n элементов по m называются такие комбинации, из которых каждая содержит m элементов и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения. Общее их число находят по формуле  где где Правило умножения. Если требуется выполнить одно за другим ка-кие-то k действий, которые можно выполнить соответственно Правило сложения. Если два взаимно исключающие друг друга дей-ствия могут выполняться соответственно m или n способами, то выпол-нить любое одно из этих действий можно m+n способами. Случайное событие – это любой факт, который в результате испыта- ния может произойти или не произойти. Испытание (опыт, эксперимент) в этом определении понимается как выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. Испытание может производиться человеком, но может осуществляться и независимо от чело- века. Человек в этом случае выступает в роли наблюдателя. События обозначаются прописными (заглавными) буквами латин-ского алфавита А, В, С, …. Достоверное событие – если в результате испытания оно обязательно должно произойти. Невозможное событие – если в результате испытания оно вообще не может произойти. События называются несовместными, если наступление одного из них исключает появление других в том же испытании. В противном случае события – совместные. Несколько несовместных событий образуют полную группу событий, если в результате испытания появится хотя бы одно из них. События, составляющие полную группу событий, называются равно-возможными, если в данном испытании ни одно из них не является более возможным, чем другое. Противоположные события – два события А и Предполагается, что на рассматриваемом множестве событий могут быть определены: сумма событий А и В (обозначается А+В =С) – событие С, состоящее в том, что произойдет хотя бы одно из событий А и В; произведение событий А и В (обозначается АВ = D) – событие D, состоящее в том, что произойдут оба события А и В. Событие испытания считается элементарным, если его нельзя пред-ставить с помощью определенных выше операций через другие события. Численная мера возможности наступления события А называется его вероятностью и обозначается Классическое определение вероятности события А: где n – общее число равновозможных исходов испытания (элементарных событий), m – число равновозможных исходов, благоприятствующих со-бытию А. Статистическое определение вероятности события А: (вероятностью события А называется число, около которого группируют-ся значения частоты данного события в различных сериях большого числа испытаний). Два события А и В называются независимыми, если вероятность со- бытия А не зависит от того, произошло событие В или нет. В противном случае события А и В называются зависимыми. Вероятность события В, найденная при условии, что событие А прои-зошло, называется условной вероятностью и обозначается Если события А и В несовместны, то стей); совместны, то независимы, то зависимы, то Если события 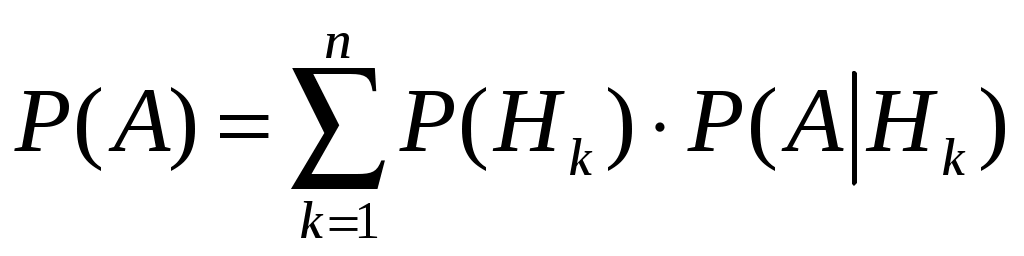 (формула полной вероятности), (формула полной вероятности),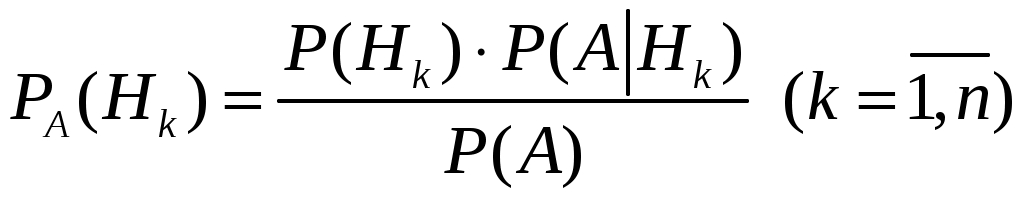 (формула Байеса). (формула Байеса).Раздел 2. Случайные величины Случайной величиной (СВ) Х называется величина, которая произвольно принимает одно из возможного множества своих значений, заранее неизвестное. Эти значения могут быть расположены дискретно (дискретная случайная величина) или заполнять интервалы (непрерывная случайная величина). Случайная величина обозначается конечными заглавными буквами латинского алфавита Х, Y, Z,…, а их значения – соответствующими строч-ными буквами х, у, z,.... Всякое соотношение, устанавливающее связь между возможными зна-чениями случайной величины и соответствующими им вероятностями, называется законом распределения случайной величины. Для дискретной случайной величины закон распределения может быть задан в виде таблицы (ряда распределения), графически (многоугольника или полигона распределения вероятностей) и аналитически. Для того чтобы задавать вероятности значений различных случайных величин, и притом задавать их одним и тем же способом, в теории ве-роятностей используют функцию распределения случайной величины (интегральный закон распределения). Пусть Х – случайная величина, х – произвольное действительное чис- ло. Вероятность того, что Х примет значение, меньшее х, называется функ- цией распределения вероятностей случайной величины: Свойства функции распределения: 10. 20. 30. 40. того, что случайная величина примет значение х, равна скачку функции распределения в точке х). Плотностью вероятности или плотностью распределения f(x) непре-рывной случайной величины Х называется производная ее функции рас-пределения: f(x) = F(x) (ее также называют дифференциальной функцией распределения). Свойства плотности вероятности: 10. f(x) 0. 20. Площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице. 30. Р(а Х b) = Математическим ожиданием дискретной случайной величины Х на-зывается сумма произведений всех её конечных возможных значений на их вероятности: 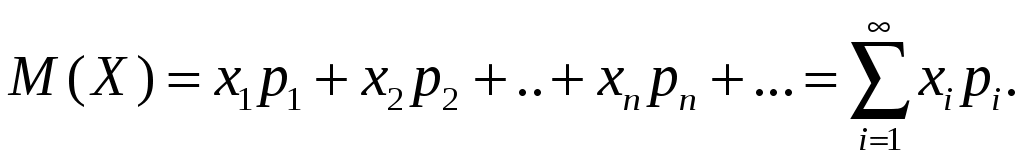 Для непрерывной случайной величины математическое ожидание имеет вид: где Дисперсией (рассеянием) СВ Х называют математическое ожидание квадрата отклонения Х от её математического ожидания: Для непрерывной случайной величины 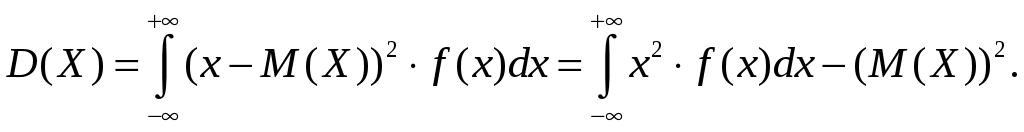 Свойства математического ожидания (а, b – константы, X, Y – случай-ные величины): 10. М(а) = а. 20. М(bX) = bМ(X). 30. М(a + bX) = a + bМ(X). 40. М(X + Y) = М(X)+М(Y). 50.М(X – М(X)) = 0. Случайные величины X и Y независимы, если Р(Х = х, Y = y) = P(X=x) Р(Y= y) для любых значений х и у. 60. М(X Y) = М(X) М(Y), если Х и Yнезависимы. 70. М[(X – М(X)) (Y – М(Y)] = 0. Свойства дисперсии: 10. D(а) = 0. 20. D(bX) = b2 D(X). 30. D(a + bX) = b2D(X). 40. D(X + Y) = D(X) + D(Y), если Х и Y независимы. Корень квадратный из дисперсии Распределение Бернулли Производится один опыт (или наблюдение), в котором может прои-зойти или не произойти событие А. Вероятность того, что событие А произойдет, равна числу p. Один такой опыт, в котором возможны лишь два исхода, называемые «успех» и «неудача», называют испытанием Бер-нулли. Пусть случайная величина Х характеризует появление события А в данном опыте, т.е.  Тогда говорят, что СВ Х распределена по закону Бернулли и Производится n независимых опытов, в каждом из которых может произойти (с вероятностью p) или не произойти (с вероятностью 1–p) не-которое событие А, т.е. производится n независимых испытаний Бер-нулли. Повторные независимые испытания называют схемой Бернулли (схема названа в честь Я. Бернулли, доказавшего свою теорему в 1713 г. для такой последовательности испытаний). Рассмотрим случайную величину Х, равную числу «успехов» в схеме Бернулли. Найдем вероятность Pk того, что в n испытаниях Бернулли бу-дет k «успехов», или, что то же самое, что случайная величина Х примет значение, равное k. Рассмотрим событие Вk, состоящее в том, что Х=k, т.е. событие А поя- вится в опытах ровно k раз. Событие Вk может осуществляться различными способами. Разложим событие Вk на сумму произведений событий, состоящих в появлении или непоявлении события А в отдельном опыте. Будем обозначать через Аi появление события А в i-м опыте; Каждый вариант появления события Вk (т.е. каждый член суммы раз-ложения Вk) должен состоять из k появлений события А и n-k непояв-лений, т.е. из k событий А и n-k событий  – числу способов, какими можно из n опытов выбрать k, в которых произошло событие А. Вероятность каждой такой комбинации по теореме умножения для независимых событий равна – числу способов, какими можно из n опытов выбрать k, в которых произошло событие А. Вероятность каждой такой комбинации по теореме умножения для независимых событий равна Таким образом, Имеем: Эту формулу называют формулой Бернулли, а относительно случай-ной величины Х говорят, что она имеет биномиальное распределение. Закон Пуассона Дискретная случайная величина Х распределена по закону Пуассона, если вероятность того, что она примет конкретное значение m, опреде-ляется соотношением 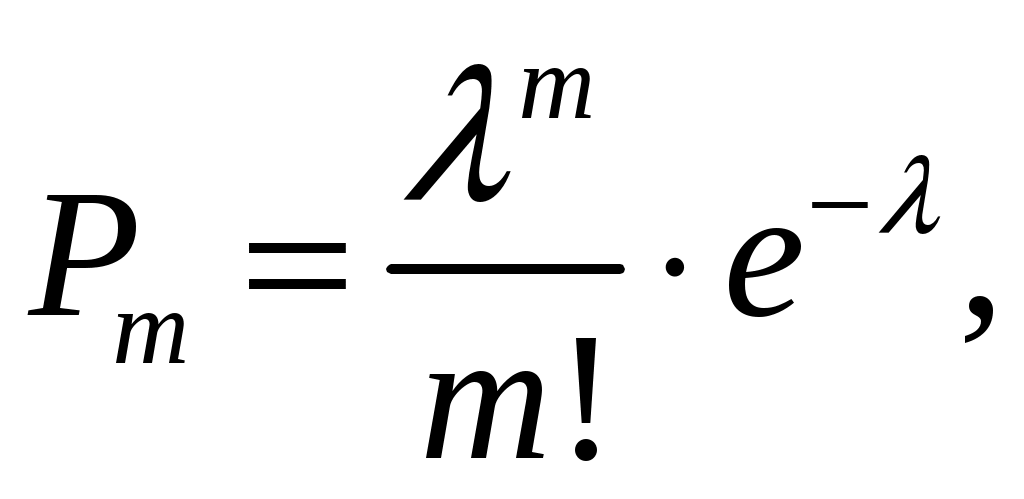 где где Закон равномерной плотности Непрерывная случайная величина Х называется равномерно распре-деленной на промежутке [a,b], если ее плотность вероятности на этом про-межутке постоянна, а вне промежутка равна нулю (рис. 1). 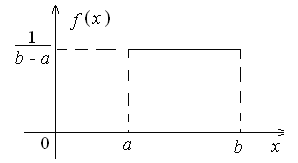 Рис. 1. График плотности Имеем: Нормальный закон распределения Непрерывная случайная величина Х имеет нормальное распределение с параметрами m и  . .Нормальный закон распределения (также называемый законом Гаусса) играет исключительную роль в теории вероятностей. Главная особенность, выделяющая нормальный закон среди других законов распределения вероятностей, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Рассмотрим смысл параметров нормального распределения. Параметр m является центром симметрии распределения. При изменении знака разности (x–m) на обратный выражение для плотности нормального распределения не меняется. Если изменять значения параметра m, то кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы. Таким образом, центр рассеивания характеризует положение распределения на оси абсцисс (рис. 2). 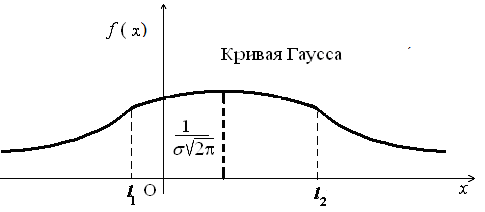 Рис. 2. График плотности Параметр Вероятность попадания случайной величины на заданный интервал выражается через плотность распределения:  . .Последний интеграл не выражается через элементарные функции. Упростим сначала подынтегральное выражение, сделав замену переменной 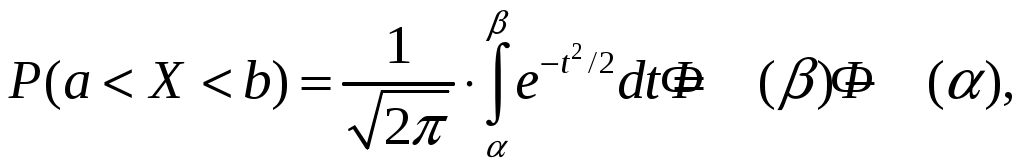 (2.2) (2.2)где 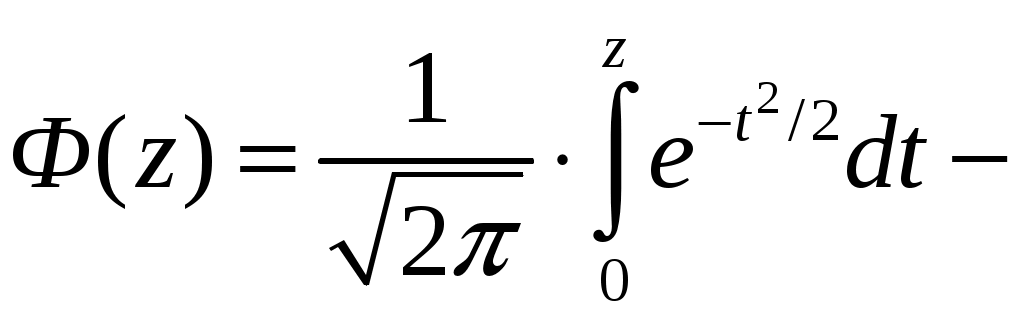 функция распределения с параметрами 0 и 1 (функция Лапласа). Эта функция затабулирована и приведена в Приложе-нии 1 (заметим, что эта функция приведена лишь для положительных значений z. Для отрицательных значений z следует воспользоваться свой-ством четности функции, т.е. функция распределения с параметрами 0 и 1 (функция Лапласа). Эта функция затабулирована и приведена в Приложе-нии 1 (заметим, что эта функция приведена лишь для положительных значений z. Для отрицательных значений z следует воспользоваться свой-ством четности функции, т.е. Имеем:M(X) = m, D(X) = 2. Правило трех сигм: если случайная величина Х имеет нормальный за- кон распределения с параметрами m и 2, то практически достоверно (вероятность 0,9973), что ее значения заключены в интервале (m–3, m+3). Показательное (экспоненциальное) распределение Непрерывная случайная величина Х имеет показательное (экспонен-циальное) распределение, если ее плотность распределения имеет вид:  где >0 – параметр распределения (рис. 3). Имеем: M(X) = 1/, D(X) = 1/2,(X) = 1/. Раздел 3. Случайные векторы Мерой взаимосвязи двух случайных величин Х и Y может служить ко- эффициент ковариации: Cov(X,Y)= xy = M[(X–M(X))(Y–M(Y))] =M(XY) –M(X)M(Y). 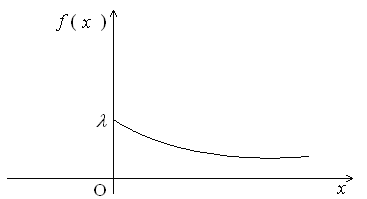 Рис. 3. График плотности Если случайные величины Х и Y независимы, то Cov(X,Y)=0 (при этом обратное утверждение, вообще говоря, неверно!). Более точной мерой линейной зависимости между величинами яв-ляется безразмерный коэффициент корреляции xy: xy =  Свойства коэффициента корреляции: 10. -1 20. 30. Если Х и Y – независимые величины, то xy = 0. В этом случае говорят, что эти величины не коррелируют. Если xy и Y коррелированы. Раздел 5. Цепи Маркова Случайной функцией (процессом) X(t) называется функция, значение которой при каждом значении аргумента t является случайной величиной. Случайная функция X(t) называется строго стационарной, если вероят- ностные характеристики случайной функции X(t+t) при любом t тожде- ственно совпадают с соответствующими характеристиками случайной функции X(t). Случайная функция X(t) называется стационарной в широком смысле, если ее математическое ожидание, дисперсия и автоковариационная (авто-корреляционная) функция не меняются во времени. Пусть имеется некоторая система (некоторый объект) S, которая в каж-дый момент времени находится в одном из состояний. Состояние системы меняется с течением времени случайным, заранее непредсказуемым об-разом. Это значит, что в системе S протекает случайный процесс. Случайный процесс, протекающий в системе S, называется марков-ским («процессом без последействия» или «без памяти»), если он обладает следующим свойством: для каждого момента времени t0 вероятность лю-бого состояния системы в будущем (при t>t0) зависит только от ее сос-тояния в настоящем (при t=t0) ине зависит от того, когда и каким образом система пришла в это состояние, т.е. как развивался процесс в прошлом. Марковские случайные процессы делятся по различным признакам в зависимости от того, как и в какие моменты времени система S может менять свои состояния. Состояния системы могут изменяться либо дискрет-но, либо непрерывно. Случайный марковский процесс называется процессом с дискретными состояниями, если возможные состояния системы S1,S2,S3,, можно пере-числить (пронумеровать) одно за другим, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) перескакивает из одного состояния Si в другое состояние Sj (например, работа часового механизма). Случайный марковский процесс с непрерывным, постепенным изменени-ем состояний называется марковским с непрерывными состояниями (процесс движения корабля, самолета, автомобиля, процесс непрерывного производства). Случайный марковский процесс называется процессом с дискретным временем, если переходы системы из состояния в состояние возможны только в точно определенные, заранее фиксированные моменты времени t1, t2,… . В промежутки времени между этими моментами система S сохраня-ет свое состояние. Случайный процесс называется процессом с непрерывным временем, если переход системы из состояния в состояние возможен в любой, напе-ред неизвестный, случайный момент времени t. Любой марковский процесс описывают с помощью вероятности состо- яний и переходных вероятностей. В системе с дискретными состояниями переход из состояния в состо- яние может происходить либо в определенные фиксированные моменты, либо в случайные моменты времени. Пусть имеется система S, которая может находиться в состояниях S1, S2,S3,,Sn, причем переходы из состояния в состояние возможны только в моменты времени t1,t2, ,tk, . . Так как времена t1, t2, фиксированы, то случайный процесс можно рассматривать как функцию целочисленного аргумента k (k =1, 2, ) (номера шага). Случайный процесс, происходя-щий в системе, состоит в том, что в последовательные моменты времени t1,t2, система S оказывается в разных состояниях, например, следующим образом: S1S3S5S2 , где стрелками указано направление перехода из состояния в состояние. В моменты времени t1,t2, система может не только менять свое состояние, но и оставаться в прежнем состоянии, например S1S1S3S5S2S1 . Процесс, протекающий в такой системе, можно рассматривать как по-следовательность (цепочку) событий или состояний, который может быть изображен следующим образом: Число в скобках означает номер шага, нижний индекс обозначает но-мер состояния. Переход из одного состояния в другое осуществляется слу-чайным образом и может быть описан с помощью вероятности. В некото-рых системах вероятность перехода в другие состояния не зависит от того, в каком состоянии была перед этим система. В других системах такое ут-верждение оказывается неверным. Случайная последовательность событий с фиксированным шагом на-зывается дискретной марковской цепью, если для каждого шага вероят-ность перехода из любого состояния Si в любое другое состояние Sj не зависит от того, когда и как система пришла в состояние Si. Следовательно, цепью Маркова является марковский случайный процесс с дискретным временем и дискретным конечным множеством состояний. Она является простым случайным процессом. Если переход системы из одного дискретного состояния в другое происходит не в строго фиксированные, а в случайные моменты времени, то применяется схема марковского процесса с дискретными состояниями и непрерывным временем. Такая схема или такой процесс называется непре-рывной цепью Маркова или марковским процессом. Пусть имеется некоторая система S с дискретными состояниями S1, S2,S3,,Sn. Будем изображать каждое состояние кругом, а возможные пере-ходы (перескоки) из состояния в состояние – стрелками. Стрелками отме-чаются только непосредственные переходы из состояния в состояние. Если же система может перейти из состояния S1 в состояние S3 только через S2, то стрелками отмечаются только переходы из S1 в S2 и из S2 в S3, но не из S1 в S3 . При этом в некоторых случаях ставят буквенные (вероятности переходов из состояния в состояние) или цифровые обозначения (время переходов, интенсивности переходов, т.е. среднее число переходов в еди- ницу времени и др.). Пусть система S может находиться в одном из состояний S1,S2,,Sn. Для Марковских процессов с дискретным временем в некоторый k-й мо- мент времени (tk на k-м шаге) система будет в одном из возможных состояний, т.е. осуществляется одно событие из полной группы несовместных событий или называются вероятностями состояний системы на k-м шаге. Так как име-ется полная группа несовместных событий, то Для марковских случайных процессов с непрерывным временем (не-прерывных марковских цепей) аргументом функции вероятности состоя-ния будет не номер шага, а текущее время, т.е. для n состояний имеется nвероятностей В случае дискретной марковской цепи для любого шага существуют еще вероятности перехода системы из одного состояния в любое другое. Эти вероятности называются переходными вероятностями марковской цепи. Некоторые из переходных вероятностей оказываются равными нулю. Это значит, что из данного состояния в другое состояние система не может перейти никогда. Вероятность перехода из состояния Si в состояние Sjобозначается Так как состояния, чаще всего, нумеруют целыми числами и обозна- чают i, j, то вероятности перехода обозначают pij. Если переходные вероятности не зависят от номера шага, то мар-ковская цепь называется однородной, в противном случае – неоднородной. Переходные вероятности цепи Маркова за один шаг рij, имеют два индекса, поэтому их записывают в виде матрицы Р=[рij], которую называют матрицей вероятностей перехода или просто переходной матри-цей: 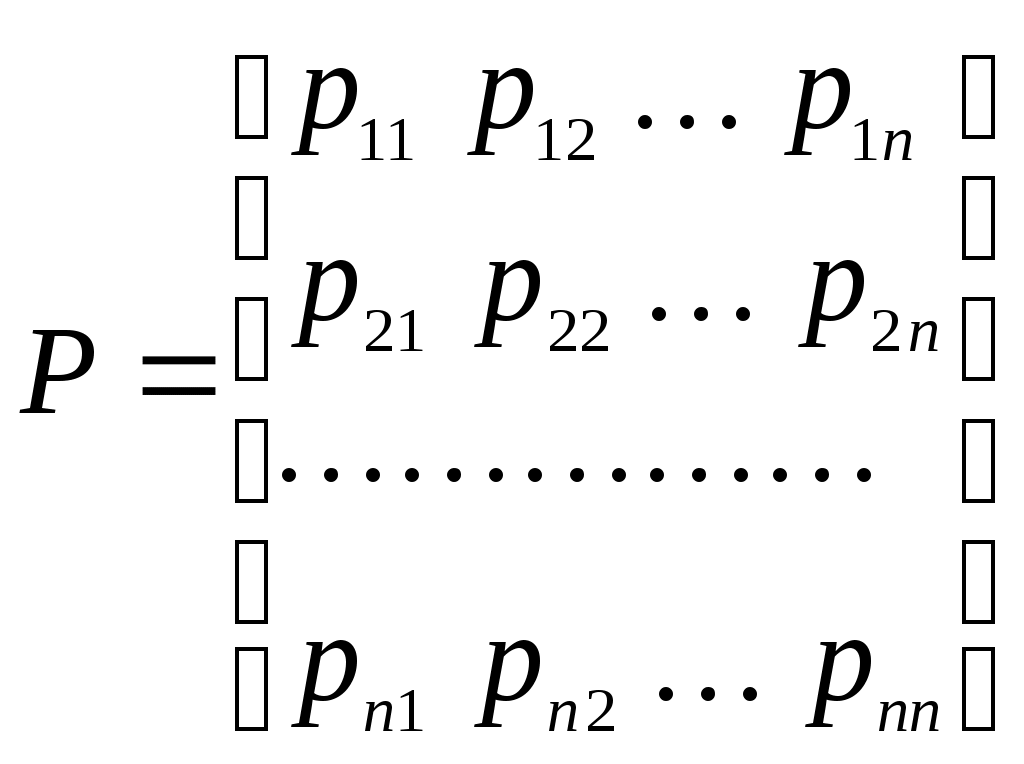 . .В зависимости от того, конечно или бесконечно число состояний, то и сама матрица Р – либо конечна, либо бесконечна. Элементы матрицы обла- дает следующими свойствами: 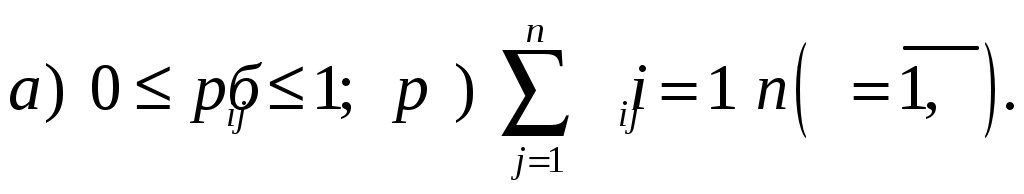 Матрицы с такими свойствами часто называют стохастическими. Матрицы переходов позволяют вычислить вероятность любой траек-тории (реализации) цепи Маркова с помощью теоремы умножения вероят-ностей. Для однородных цепей Маркова матрицы переходов не зависят от времени. Имея матрицу переходных вероятностей, и зная начальное сос-тояние системы, можно найти вероятности состояний на любом k-м шаге для дискретной марковской цепи. Рассмотрим однородную цепь Маркова с n состояниями. Для полу-чения вероятности перехода из состояния Si в состояние Sjза m шагов в соответствии с формулой полной вероятности следует просуммировать произведения вероятности перехода из состояния Si в промежуточное состояние Skза l(0 l m) шагов на вероятность перехода из Skв Sjза оставшиеся т–lшагов: (суммирование ведется по всем постоянным k) Например, переход из состояния i в состояние j за m=2 шага осуще-ствляется следующим образом: 1-й шаг – переход из iв некоторое проме- жуточное состояние k, 2-й – переход из k в j. В частности, полагая l=1 и l= m –1, получим две формулы: Формулы (2.3) и (2.4) в общем случае позволяют найти вероятность перехода за любое число шагов, если предварительно определены вероят-ности перехода за меньшее число шагов. При фиксированном значении m запись массива вероятностей pij(m) можно оформить в виде следующей матрицы: 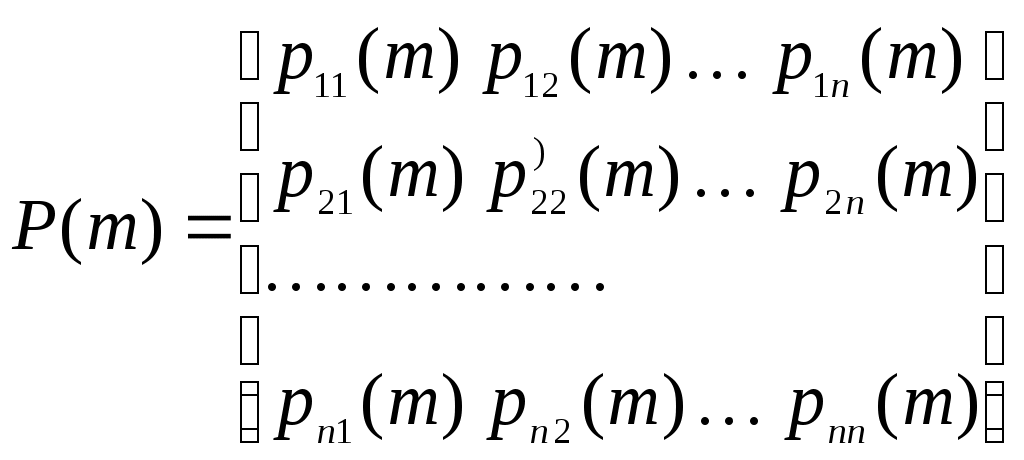 . .Таким образом, имеем: P(2) = p(l) p(l) = p2, P(3) = p(2) p(l) = p(1) p(2) = p3,…, P(m) = p(m–1) p(l) = p(1) p(m–1) = pm, что дает возможность найти вероятности перехода между состояниями за любое число шагов, зная матрицу переходов за 1 шаг. Зная матрицу переходов за m шагов и начальное положение системы, можно найти вероятность находиться на шаге m в любом состоянии Sj(j= 1,2,..., n): где p0(i) – вероятность находиться в начальный момент времени в состо-янии Si; pij(m) –вероятность перейти из состояния Siв состояние Sjза mшагов – элемент матрицы P(m). Рассмотрим вероятности перехода из данного исходного состояния в данное заключительное. Предположим, что исходное состояние испытате-лю не известно. Пусть дано распределение вероятностей исходного состоя-ния в виде где 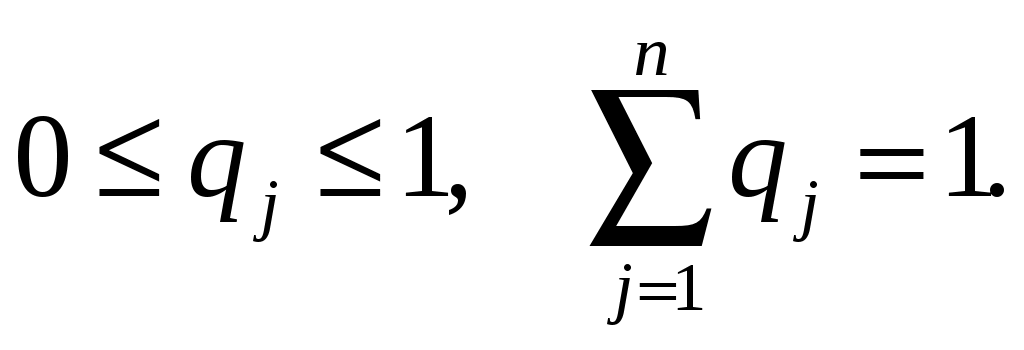 Случай, когда исходное состояние полностью определено, соответ- ствует тому, что одна из компонент стохастического вектора Пусть чала функционирования окажется в j-м состоянии, если его начальное состояние задано вектором При этом Возникают вопросы: что будет происходить с системой при m ®¥? будут ли вероятности pl(m),p2(m),...,pn(m)стремиться к каким-то пределам? Эти пределы, если они существуют, называются предельными вероят-ностями состояний. Существует теорема: а) если в цепи Маркова из каждого состояния можно перейти (за то или иное число шагов) в каждое другое, то предельные вероятности состо- яний существуют и не зависят от начального состояния системы; б) вектор p, составленный из предельных вероятностей, должен удовлетворять соотношению p= p Р. Таким образом, при m ®¥ всистеме устанавливается некоторый пре- дельный стационарный режим, который состоит в том, что система слу-чайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени: каждое из состояний осуществляется с неко-торой постоянной вероятностью. Среднее время пребывания в состоянии Siза время Т равно piT, где рi–предельная вероятность состояния Si. Среднее время возвращения в состояние Siравно 1/pi. |
