Машфак. ТВ иМС для МСФ. Исследование связи между показателями, часть из которых являются случайными
 Скачать 2.07 Mb.
|
|
Решение. Так как по условию задачи задана  , то для нахождения доверительного интервала воспользуемся формулой  Все величины, кроме t, нам известны из условия. Для нахождения t воспользуемся соотношением  По таблице функции Лапласа (Приложение 1) находим, что  соответствует значение  Подставив в формулу для доверительного интервала значения пара- метров, получим:  или  Пример 3.11. Проверить гипотезу о числовом значении математического ожидания нормального распределения. Решение. Имеем  причем числовое значение а неизвестно, а числовое значение дисперсии  известно.Случай 1: Этап1.  Этап2.Зададимся уровнем значимости  .Этап3. В качестве критерия возьмем величину 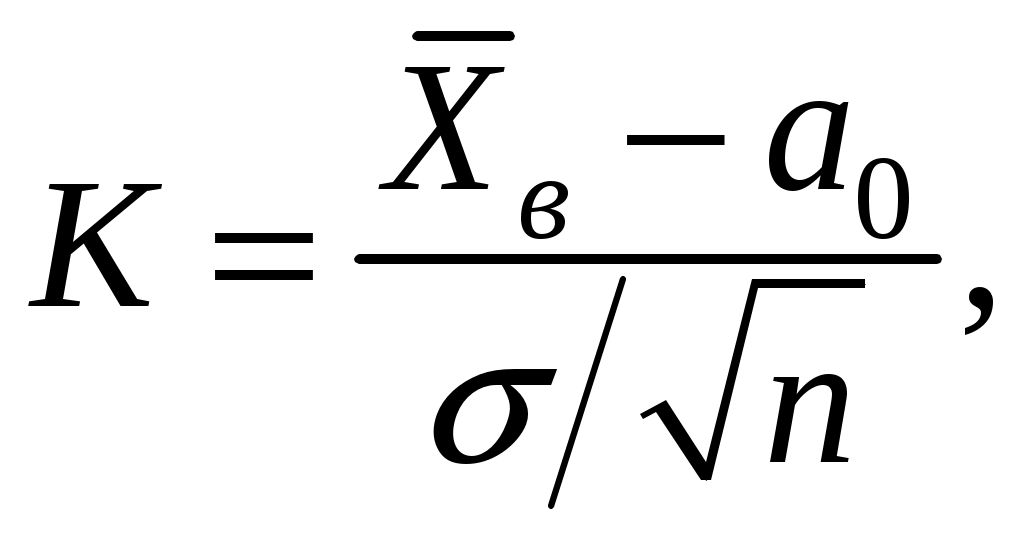 значение которой зависит от выборочных данных, является случайной и при выполнении гипотезы 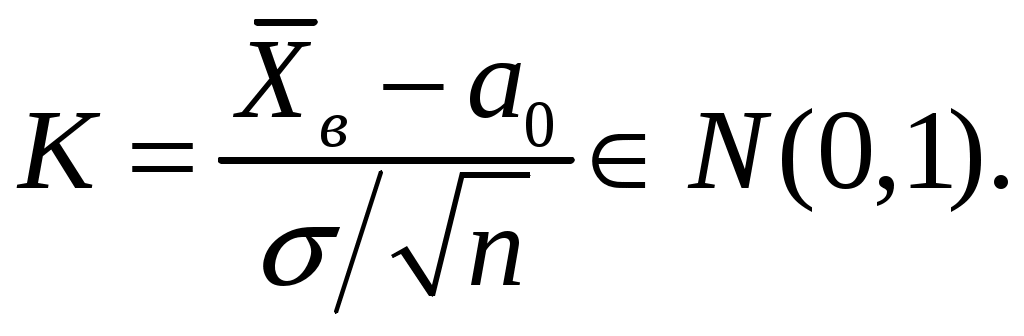 подчиняется нормальному распределению N(0,1), т.е.  Этап4. Построим критическую область, она будет правосторон-ней: ее образует интервал  , где  определяется из условия  Находим значение , удовлетворяющее уравнению  Этап5. Используя вместо  конкретные числа, находим  а затем численное значение  критерия. Если  то гипотеза  отвергается и принимается гипотеза  Случай 2: Этап1.   Этап2. Зададимся уровнем значимости  Этап3. В качестве критерия, как и в случае 1, возьмем величину 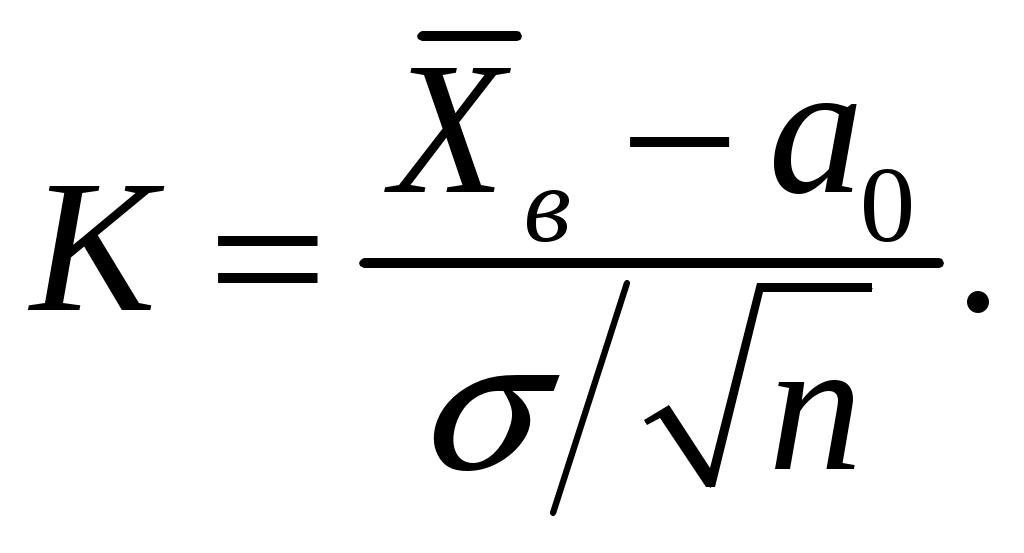 Этап 4. Критическая область будет двусторонней: ее образуют ин-тервалы 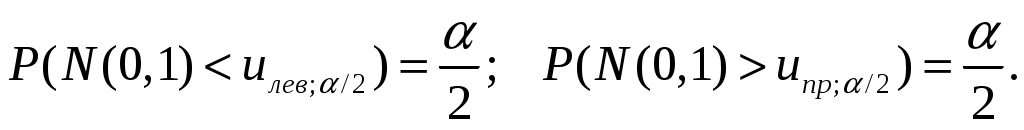 и  , где критические точки  и  находятся из условия Находим из условия  В силу симметричности функции плотности распределения  имеем  .Этап5. Находим числовое значение критерия. Если попадает в интервал  или  то гипотеза отвергается и принимается альтернативная. Пример 3.12. Проверить гипотезу о числовом значении математичес-кого ожидания при неизвестной дисперсиинормального распределения. Решение. Имеем 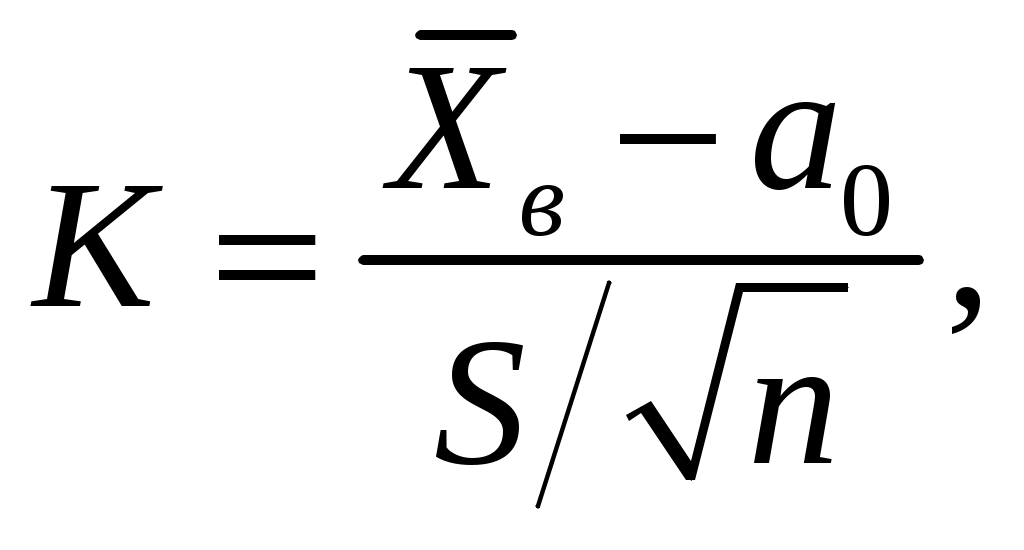причем числовое значение а неизвестно, а числовое значение дисперсии также неизвестно. В этом случае за ос-нову проверки гипотезы  где а0 – заранее заданное число, положен критерий имеющий при выполнении гипотезы t-распределение с числом степеней свободы  . Задаваясь уровнем значимости  построим критическую область для проверки гипотезы при следующих альтернативных гипотезах.Случай 1: Альтернативная гипотеза  Критическая область является правосторонней: ее образует интервал  где точка  определяется из условия  В Приложении 4 приведены значения t. Так как функция плотности t-распределения симметрична относительно нуля, то искомая точка определяется как  .Вычислим значение критерия . Если  , то гипотеза отвергается и принимается гипотеза Случай 2: Альтернативная гипотеза имеет вид Критическая область состоит из двух интервалов  и  где критические точки  и  определяются из условий   Обращаясь к Приложению 4, находим:  ,  Вычислим значение критерия . Если попадает в интервал или  , то гипотеза отвергается и принимается альтернативная гипотеза Если  [ ], то принимается основная гипотеза  Пример 3.13. Проверить гипотезу о числовом значении дисперсии нормального распределения. Решение. Выборочная оценка 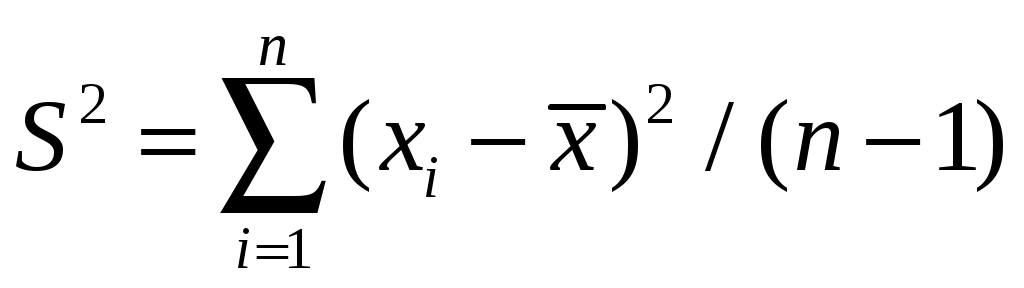 дает приближенное представление 2. Используя эту оценку, проверим гипотезу  где  – заранее заданное число. В качестве критерия возьмем случайную величину 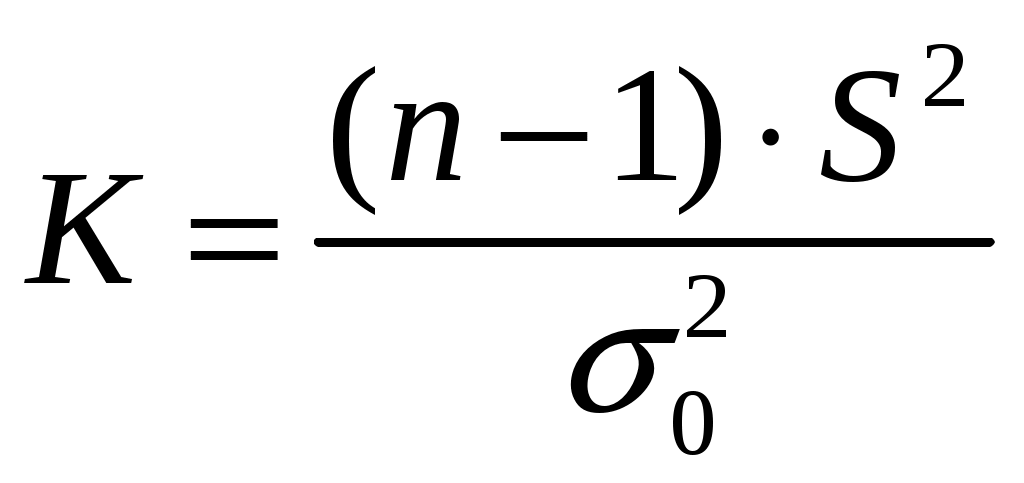 ,имеющую при выполнении гипотезы 2-распределение с числом степеней свободы  . Зададимся уровнем значимости и перейдем к построению критических областей для проверки гипотезы H0 при следующих двух альтернативных гипотезах H1.Случай 1: В качестве альтернативной гипотезы примем  Критическая область является правосторонней и определяется интервалом  где критическая точка  находится из условия  . Следовательно, искомая критическая точка  находится как Находим . Если  то гипотеза H0 отвергается и прини-мается гипотеза H1. Случай 2: В качестве альтернативной гипотезы примем  В этом случае критическая область состоит из двух интервалов  и  где критические точки  и  определяются из условий   Обращаясь к соответствующей таблице, находим   Если значение попадает в один из интервалов или  , то гипотеза H0 отвергается и принимается гипотеза H1. В противном случае нет оснований отвергнуть гипотезу H0.Пример 3.14. Проверить нулевую гипотезу о том, что заданное зна-чение  является математическим ожиданием нормально распре-деленной случайной величины при 5%-м уровне значимости для двусто-ронней критической области, если в результате обработки выборки объёма n = 64 получено выборочное среднее  , а генеральное среднее квад-ратичное отклонение равно  равно 1.Решение. В данной задаче речь идёт о проверке гипотезы о числовом значении математического ожидания нормального распределения при известной дисперсии, т.е. о сравнении гипотетической (предполагаемой) генеральной средней 21 с выборочной средней 16 при известном среднем квадратичном отклонении  .Нулевая гипотеза в этой задаче имеет вид:  : , а альтерна-тивная –  : . Уровень значимости задан:  .В качестве критерия в этом случае рассматривается функция  .Функция  подчинена нормальному закону распределения  . Критическая область будет двусторонней, её образуют интервалы  и  , определяемые из условий  и  .Если , то  , т.е. имеем вероятность попадания слу-чайной величины  в левостороннюю или правостороннюю критические области. В этом случае вероятность непопадания случайной величины в правостороннюю критическую область можно представить следующим образом: .Так как  , а  – функция Лап-ласа в точке  , то  . На основании таблицы значений функции Лапласа (Приложение 1) находим:  . Точка  расположена симметрично и равна -1,96. Следовательно, критическая область состоит из интервалов  и  . Рассчитаем  : .Значение попадает в критическую область, поэтому гипотеза : отвергается и принимается альтернативная гипотеза Н1. |