Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
1.2. Определение устойчивости цифровых систем в форме z-преобразованияДля устойчивости дискретной системы необходимо и достаточно, чтобы все корни характеристического уравнения замкнутой системы (полюса передаточной функции замкнутой дискретной системы) удовлетворяли условию: 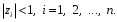 (1.1) (1.1)Если хотя бы один корень 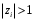 , система будет неустойчивой. Значением какого-либо корня , система будет неустойчивой. Значением какого-либо корня 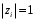 при всех остальных при всех остальных 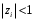 определяется граница устойчивости дискретной системы [3, 10, 13]. определяется граница устойчивости дискретной системы [3, 10, 13].Графически область устойчивости дискретной системы на плоскости Z корней характеристического уравнения изображается единичным кругом на рисунке 1. 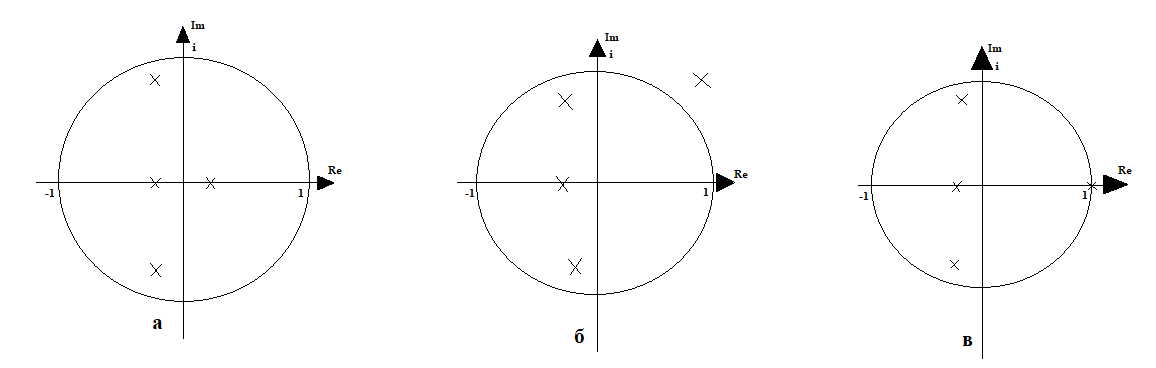 Рис. 1. Области устойчивости на плоскости Z: a – устойчивой, б – неустойчивой, в – на границе устойчивости. Таким образом, исследование устойчивости сводится к изучению расположения корней характеристического уравнения дискретной системы относительно единичной окружности. Сопоставим, как выглядят передаточные функции для дискретных и непрерывных систем. Передаточная функция – функция комплексного переменного z, произведение которого на z - преобразование входного сигнала системы дает z -преобразование выходной величины. Для непрерывных систем передаточная функция имеет вид дробно-рациональной функции от s преобразования Лапласа: 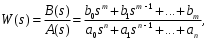 (1.2) (1.2)где a0, a1, …, an, b0,b1, …, bn - коэффициенты; A(s) и B(s) – изображение по Лапласу; m, n – целые положительные числа (m ≤ n). Характеристическое уравнение 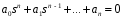 представляет собой степенное уравнение, при этом число корней уравнения равно степени полинома - n. представляет собой степенное уравнение, при этом число корней уравнения равно степени полинома - n.Для того чтобы получить преобразование Лапласа импульсивного сигнала на выходе системы, воспользуемся уравнением последовательности идеальных импульсов: 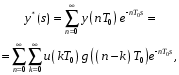 (1.3) (1.3)где T0 – такт квантования; k, n – индексы дискретного времени k = t / T0 = 0, 1, 2, …; g - импульсная реакция (весовая функция); s – переменная преобразования Лапласа (s = σ + iω) или сигнал, u – входной сигнал объекта. Подставив в эту формулу параметр q = n - k: 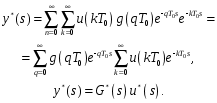 (1.4) (1.4)Отсюда 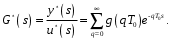 (1.5) (1.5)Переходя к переменной 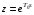 , введем дискретную функцию по переменной z: , введем дискретную функцию по переменной z: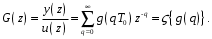 (1.6) (1.6)Динамические свойства линейной стационарной системы с сосредоточенными параметрами полностью определяются его дифференциальным уравнением, имеющим вид 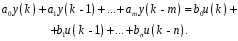 (1.7) (1.7)Тогда дискретная передаточная функция будет иметь вид: 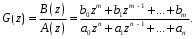 (1.8) (1.8)Характеристическое уравнение 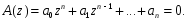 (1.9) (1.9)представляет собой трансцендентное уравнение, при этом число корней уравнения бесконечно, так как они имеют периодический характер [3, 12]. Устойчивость линейных дискретных систем с постоянными коэффициентами может быть изучена как в плоскости s, так и в плоскости z. В плоскости s критерием устойчивости может быть то, что полюсы системы находятся в ее левой половине. В дискретных системах предполагают, что система является устойчивой, если полюс расположен на плоскости z в области меньшей единице. Этот критерий плоскости z вытекает из того факта, что левая половина плоскости s отображается внутренней частью единичной окружности по плоскости z[4, 11]. Это следует из рисунка 1 и соотношения 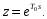 (1.10) (1.10) |
