Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич

• Название: Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
• Дата: 14.12.2022
• Размер: 0.49 Mb.
• Имя файла: Диплом Лоренц Степанова.docx
• Тип: Исследование; #844826
• страница: 10 из 11

3.5. Критерий устойчивости Шур - Кона

Пример 10. Определить устойчивость дискретной системы, если передаточная функция в форме z – преобразования, имеет вид: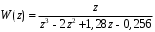

.

Решение: По условию данного критерия, линейная дискретная система устойчива, если коэффициенты характеристического уравнения удовлетворяют всем отрицательным определителям с нечетными индексами и положительными определителям с четными индексами.

Характеристическое уравнение имеет вид: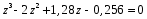

.

Составляем определители Шур - Кона по формулам (2.29), (2.30):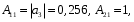



Следовательно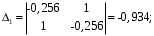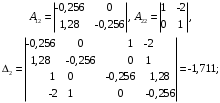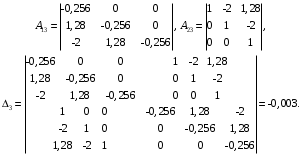







Все полученные определители оказались отрицательными, что опровергает условию критерия Шур - Кона. Следовательно, система является неустойчивой.

Пример 11. Определить устойчивость дискретной системы, если передаточная функция в форме z – преобразования, имеет вид: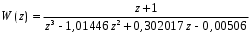

.

Решение: По условию данного критерия, линейная дискретная система устойчива, если коэффициенты характеристического уравнения удовлетворяют всем отрицательным определителям с нечетными индексами и положительными определителям с четными индексами.

Составляем определители Шур - Кона по формулам (2.29), (2.30):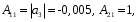



Следовательно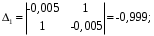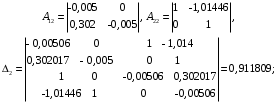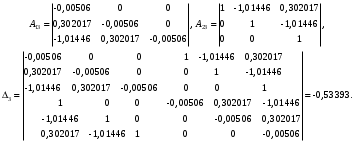







Определители с нечетными индексами оказались отрицательными, а с определитель с четным индексом – положительным, что подтверждает условию критерия Шур - Кона. Следовательно, система является устойчивой.

3.6. Применение критерия устойчивости Гурвица

Пример 12. С помощью критерия Гурвица определить устойчивость дискретной системы, если передаточная функция дискретной системы имеет вид: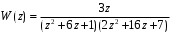

.

Решение: Согласно данному критерию линейная дискретная система устойчива, если при 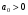определитель Гурвица и все его диагональные миноры положительны. Значит, первым делом необходимо найти а₀.

Характеристическое уравнение системы имеет вид: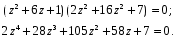



Все коэффициенты характеристического уравнения положительны, следовательно, выполняется необходимое условие устойчивости. Но оно является недостаточным, т.к. характеристическое уравнение имеет 4-й порядок. Следующим шагом будет нахождение всех диагональных миноров определителя Гурвица 4-го порядка.

В характеристическом уравнении выше a₀=2>0. Теперь проверяем главные миноры данной матрицы: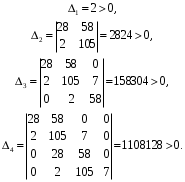



Таким образом, при a₀>0 все главные миноры определителя Гурвица положительны, что соответствует условию критерия устойчивости. Следовательно, система является устойчивой.

Пример 13. С помощью критерия Гурвица определить устойчивость дискретной системы, если передаточная функция дискретной системы в форме z – преобразования: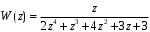

.

Решение: Согласно данному критерию линейная дискретная система устойчива, если при 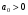определитель Гурвица и все его диагональные миноры положительны. Значит, первым делом необходимо найти а₀.

Характеристическое уравнение системы имеет вид: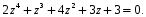



Все коэффициенты характеристического уравнения положительны, следовательно, выполняется необходимое условие устойчивости. Но оно является недостаточным, т.к. характеристическое уравнение имеет 4-й порядок. Следующим шагом будет нахождение всех диагональных миноров определителя Гурвица 4-го порядка.

В характеристическом уравнении выше a₀=2>0. Теперь проверяем главные миноры данной матрицы: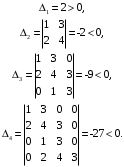



Таким образом, при a₀>0 все главные миноры определителя Гурвица, кроме первого отрицательны, что не соответствует условию критерия устойчивости. Следовательно, система является неустойчивой.