Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
ГЛАВА 2. КРИТЕРИИ УСТОЙЧИВОСТИ ЦИФРОВЫХ СИСТЕМ УПРАВЛЕНИЯ2.1 Определение критериев устойчивостиКритерии устойчивости – это косвенные методы анализа устойчивости, которые дают ответ об устойчивости системы без определения корней характеристических уравнений четвертого и более высокого порядка. Критерии устойчивости делятся на алгебраические и частотные [3, 16]. Алгебраическими критерияминазываются критерии, которые основаны на проверке определенных соотношений, составленных из коэффициентов характеристического уравнения. Поэтому при использовании алгебраических критериев нужно иметь только характеристическое уравнение. Если исследование устойчивости проводится с помощью алгебраических критериев, нужно, прежде всего, проверить выполнение необходимого условия устойчивости, так как его проверка не требует никаких вычислений и при невыполнении этого условия дальнейших исследований проводить не нужно [15, 16]. Необходимое условие устойчивости. Для того чтобы система была устойчива, необходимо, чтобы коэффициенты ее характеристического уравнения были одного знака: a0 > 0, a1 > 0 … an > 0, (2.1) Если необходимое условие не выполняется, то система неустойчива. Если же необходимое условие выполняется, то система при п ≥ 3 (п — порядок системы) может быть устойчивой и неустойчивой и для установления устойчивости нужно воспользоваться каким-либо критерием устойчивости. Как уже установлено, в случае систем первого и второго порядков необходимое условие является и достаточным. К алгебраическим критериям относятся такие критерии, как критерий Джури, Гурвица и Льенара-Шипара, который еще называют модификацией критерия Гурвица. Частотными критериями называются критерии устойчивости, основанные на построении частотных характеристик и так называемой кривой Михайлова. Частотными называют такие критерии, как критерий Михайлова, Найквиста и логарифмический частотный критерий. Эти критерии являются графоаналитическими и получили широкое распространение, т.к. позволяют легко исследовать устойчивость систем высокого порядка, а также имеют простую геометрическую интерпретацию и наглядность. Рассмотрим принципы применения алгоритмов на тестовых примерах реальных объектов с различной конфигурацией нулей и полюсов. 2.2. Критерий устойчивости ДжуриДанный критерий был назван в честь американского ученого Калифорнийского университета Э. Джури в 1955 году [11, 14]. В настоящее время нет принципиальных трудностей вычисления корней характеристического уравнения с использованием электронно-вычислительных машин, однако при необходимости экономить машинное время целесообразно пользоваться критерием устойчивости Джури, алгоритм которого состоит в следующем: 1) Пусть задан характеристический полином (1.9) при a0 > 0. Введём понятие обратного полинома, получаемого путём перестановки коэффициентов исходного в обратном порядке. 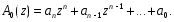 (2.2) (2.2)2)Разделим (1.9) на обратный ему полином (2.2). В итоге получим частное от деления число 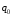 и остаток и остаток 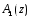 - полином n-1 степени: - полином n-1 степени: 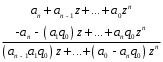 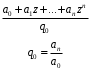 (2.3) (2.3)Домножая полученный результат 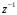 , получаем: , получаем: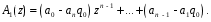 (2.4) (2.4)3) Затем делим остаток 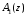 на обратный ему на обратный ему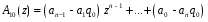 (2.5) (2.5)и определяем новые 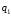 и и 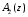 : :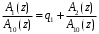 (2.6) (2.6)Выполняя деление полиномов 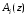 на обратные или на обратные или 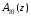 , получаем последовательность , получаем последовательность 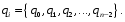 (2.7) (2.7)Необходимым и достаточным условием устойчивости цифровой системы являются неравенства: 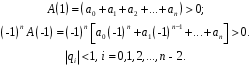 (2.8) (2.8) |
