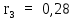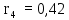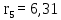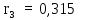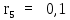Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
 Скачать 0.49 Mb.
|
3.4. Применение критерия устойчивости РаусаПример 8. С помощью критерия Гурвица определить устойчивость дискретной системы, если передаточная функция дискретной системы имеет вид: 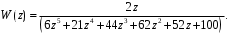 Решение: Согласно критерию Рауса линейная дискретная система устойчива, если при 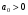 коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. были положительными. Значит, первым необходимо создать таблицы Рауса.Таблица 2. Расчет коэффициентов примера 7 с помощью критерия Рауса
Первый столбец содержит один отрицательный элемент c15 = -243,26, что опровергает условия критерия. Следовательно, дискретная система является неустойчивой. Пример 9. С помощью критерия Гурвица определить устойчивость дискретной системы, если передаточная функция дискретной системы имеет вид: 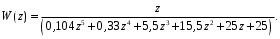 Решение: Согласно критерию Рауса линейная дискретная система устойчива, если при 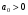коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. были положительными. Значит, первым необходимо создать таблицы Рауса.Таблица 3. Расчет коэффициентов примера 8 с помощью критерия Рауса
Первый столбец не содержит отрицательный элементов, что подтверждает выполнение условия критерия. Следовательно, дискретная система является устойчивой. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
