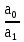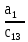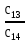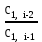Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
2.3. Критерий устойчивости РаусаЭтот критерий устойчивости был в 1877 г. предложен английским математиком Э. Раусом в виде некоторого правила (алгоритма), которое наиболее просто поясняется в таблице 1. В первой строке таблицы 1 записывают в порядке возрастания индексов коэффициенты характеристического уравнения (1.17), имеющие четный индекс: a0, a2, a4, a6, …; во второй строке - коэффициенты (1.17) с нечетным индексом: a1, a3, a5, a7, … . Любой из остальных коэффициентов таблицы определяют как 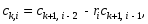 (2.9) (2.9)где 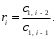 (2.10) (2.10)где k — индекс, означающий номер столбца, i — индекс, означающий номер строки таблицы 1. Таблица 1. Алгоритм критерия Рауса
Заметим, что число строк таблиц Рауса равно степени характеристического уравнения плюс единица (n+1). После того как таблица Рауса заполнена, по ней можно судить об устойчивости системы. Условие устойчивости Рауса формулируется так: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т. е. при a0 > 0 были положительными: 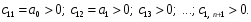 (2.11) (2.11)Если не все коэффициенты первого столбца положительны, то система неустойчива, а число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса. Критерий Рауса особенно удобен, когда заданы числовые значения коэффициентов характеристического уравнения (2.11). В этом случае определение устойчивости можно выполнить довольно быстро даже при характеристических уравнениях высокого порядка. Форма алгоритма, с помощью которого составляют таблицу Рауса, очень удобна для программирования ЭВМ, поэтому критерий Рауса нашел широкое применение при исследовании влияния на устойчивость либо коэффициентов характеристического уравнения, либо отдельных параметров системы, не очень сложным образом входящих в эти коэффициенты, с помощью быстродействующих ЭВМ. Достоинство данного критерия заключается простоте использования независимо от порядка характеристического уравнения. Он удобен для использования на ЭВМ. Его недостатком является малая наглядность, трудно судить о степени устойчивости системы, насколько далеко отстоит она от границы устойчивости [15]. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||