Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
1.3. Билинейное преобразование.Билинейное преобразование 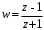 (1.11) (1.11) или 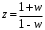 (1.12) (1.12)переводит точки единичной окружности на плоскости zв точки, лежащие на мнимой оси плоскости w, и наоборот. Любой точке, распложенной внутри этой окружности, согласно соответствует точка левой полуплоскости w, а точки, находящиеся вне окружности, отображаются в точки, принадлежащие правой полуплоскости w. Следовательно, условие устойчивости дискретной САУ, связанное с принадлежностью z-корней характеристического уравнения C(z)=0 единичному кругу, равносильно условию принадлежности левой w-полуплоскости корней уравненияC(w)=0, полученного из исходного уравнения путем билинейного преобразования: 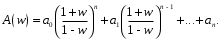 (1.13) (1.13)Расположение полюса в плоскости z определяет характер протекания процесса во временной области, так же как и местонахождение полюса в плоскости s [3]. Утверждение 1. При преобразовании 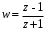 (1.14) (1.14)внутренность единичного круга на z-плоскости преобразуется в левую полуплоскость, его внешность — в правую полуплоскость и окружность (единичного радиуса) — в мнимую ось на w-плоскости. Доказательство. Представим комплексную переменную z в тригонометрической форме и подставим в (1.11): 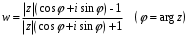 (1.15) (1.15)Преобразовав и разделив выражение справа на вещественную и мнимую части, получим 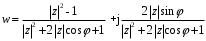 (1.16) (1.16)Так как 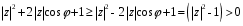 при при 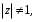 то вещественная часть то вещественная часть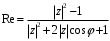 (1.17) (1.17)отрицательна при |z|<1, положительна при |z|>1 и равна нулю при |z|=1. Следовательно, при преобразовании (1.9) внутренность единичного круга z -плоскости переходит в левую полуплоскость, а его внешняя часть — в правую полуплоскость z-плоскости. Окружность единичного радиуса |z|= 1 переходит в мнимую ось. Действительно, при |z|=1 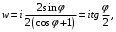 (1.18) (1.18)и при изменении 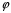 от от 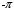 до до 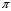 переменная v пробегает значения от переменная v пробегает значения от 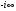 до до 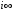 . Утверждение доказано. . Утверждение доказано.Разрешим равенство (1.12) относительно z и подставим полученное выражение в характеристическое уравнение (1.12): 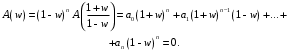 (1.19) (1.19)Представим это преобразованное характеристическое уравнение в стандартной форме: 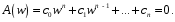 (1.20) (1.20)Выражения для коэффициентов этого уравнения через коэффициенты исходного характеристического уравнения получим, если в (1.19) раскроем скобки и произведем приведение подобных членов, а затем приравняем коэффициенты при одинаковых степенях в (1.19) и (1.20). Для п = 1,2,3 имеем: п = 1: со = ao - a1, c1=ao + a1;(1.21а) п = 2: с0 = a0 - a1 + а2,c1 = 2(а0 - а2), с2 = а0 + a1 + а2; (1.22б) п = 3: с0 = а0 - a1 + а2 - а3,c1 = 3(а0 + а3) - а1 -а2, с2 = 3(а0 - а3) + а1 - а2, с3 = а0 + a1 + а2 + а3. (1.23в) В силу утверждения 1, если корни исходного характеристического уравнения располагаются внутри единичного круга, то корни преобразованного характеристического уравнения (1.20) располагаются в левой полуплоскости. Таким образом, для того чтобы дискретная система была устойчива, необходимо и достаточно, чтобы все корни преобразованного характеристического уравнения (1.20)располагались в левой полуплоскости (имели отрицательную вещественную часть). Использование z-преобразования позволяет преобразовать трансцендентный полином в степенной, что позволяет упростить процесс исследования дискретных систем управления. Кроме того, отображает основную полосу на плоскость Z, отрезок мнимой оси 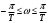 в окружность единичного радиуса, а левую часть полосы в круг единичного радиуса. в окружность единичного радиуса, а левую часть полосы в круг единичного радиуса.Решение такой задачи может быть осуществлено с использованием известных критериев, разработанных для оценки устойчивости непрерывных систем, например, критерий Гурвица или Льенара-Шипара, которые будут рассмотрены ниже. |
