Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
2.4. Критерий устойчивости Шур - КонаДанный критерий позволяет анализировать устойчивость дискретных систем по характеристическому уравнению системы, записанному в форме z-преобразования. По уравнению (1.9) запишем коэффициенты в виде определителя 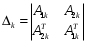 (2.29) (2.29)где 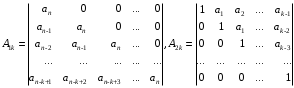 (2.30) (2.30)Дискретная система управления будет устойчивой, если коэффициенты уравнения (1.9) удовлетворяют всем определителям Шур-Кона, имеющего ∆k < 0 для нечетных k и ∆k > 0 для четных k. В этом случае система будет устойчивой [16]. Рассмотрим частные случаи: 1) При k = 1 уравнение (2.29) будет иметь вид: 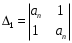 (2.30) (2.30)где A11 = an, A21 = 1. 2) При k = 2 уравнение (2.29) будет иметь вид: 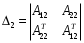 (2.31) (2.31)где 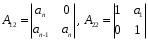 (2.32) (2.32)Тогда (2.31) записывается в виде 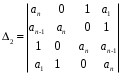 (2.33) (2.33)3) При k = 3 уравнение (2.29) будет иметь вид: 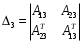 (2.34) (2.34)где 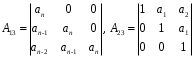 (2.35) (2.35)Тогда (2.34) записывается в виде 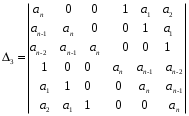 (2.36) (2.36)4) При k = 4 уравнение (2.29) будет иметь вид: 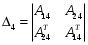 (2.37) (2.37)где 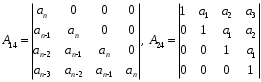 (2.38) (2.38)Тогда (2.34) записывается в виде 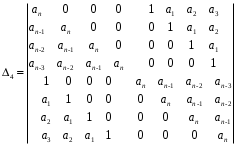 (2.39) (2.39)2.5. Критерий устойчивости ГурвицаОн был разработан немецким математиком Адольфом Гурвицом в 1895 году. Данные критерий был представлен в форме определителей, составляемых из коэффициентов характеристического уравнения системы. Рассмотри алгоритм его использования: Записываем характеристическое уравнение вида (1.9). 2. Составляем определитель Гурвица. 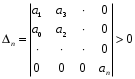 (2.12) (2.12)3. Определяем устойчивость также как и для непрерывных систем. Линейная дискретная система устойчива, если при 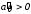 определитель Гурвица и все его диагональные миноры положительны [15, 16]. определитель Гурвица и все его диагональные миноры положительны [15, 16].Рассмотрим частные случаи. При n = 1 характеристическое уравнение имеет вид: 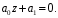 (2.13) (2.13)Определитель Гурвица имеет вид: 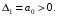 (2.14) (2.14)При n = 2 характеристическое уравнение имеет вид: 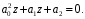 (2.15) (2.15)Определители Гурвица имеют вид: 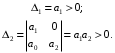 (2.16) (2.16)Как видно из рассмотренных выше случаев, при n≤2 необходимое условие устойчивости также является достаточным. При n = 3 характеристическое уравнение имеет вид: 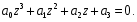 (2.17) (2.17)Определители Гурвица имеют вид: 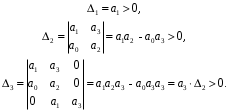 (2.18) (2.18)При n = 4 характеристическое уравнение имеет вид: 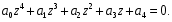 (2.19) (2.19)Определители Гурвица имеют вид: 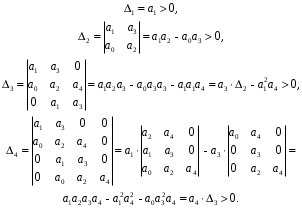 (2.20) (2.20)При 2 Критерий Гурвица применяется при n ≤ 4, т.к. при больших порядках возрастает число определителей, и процесс их нахождения становится более трудоемким. В этом случае используют ряд модификаций данного критерия, одна из которых называется критерием Льенара-Шипара. 2.6. Критерий устойчивости Льенара – ШипараКритерий устойчивости Льенара-Шипара, являющийся модификацией рассмотренного выше критерия Гурвица, был предложен П. Льенаром и Р. Шипаром в 1914 году. Его используют для определения устойчивости характеристических уравнений высоких порядков (n ≥ 5). Рассмотри алгоритм его использования: 1. Записываем характеристическое уравнение (1.9). 2. Составляем определитель Гурвица (2.12). 3. Определяем устойчивость также как и для непрерывных систем. Линейная дискретная система устойчива, если при 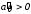 определитель Гурвица и его четные (нечетные) диагональные миноры положительны, т.е.: определитель Гурвица и его четные (нечетные) диагональные миноры положительны, т.е.:При n=2m: 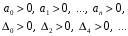 (2.21) (2.21)При n=2m+1: 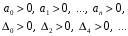 (2.22) (2.22)Рассмотрим частные случаи. При n = 5 характеристическое уравнение имеет вид: 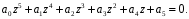 (2.23) (2.23)Вычисляем определители с четными индексами: 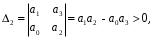 (2.24) (2.24)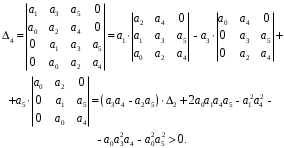 (2.25) (2.25)При n = 6 характеристическое уравнение имеет вид: 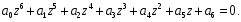 (2.26) (2.26)Вычисляем определители с нечетными индексами: 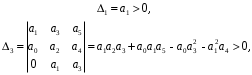 (2.27) (2.27)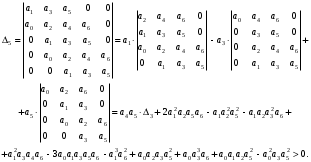 (2.28) (2.28)Данный критерий требует раскрытие меньшего числа определителей, чем у критерия Гурвица, поэтому особенно удобен при исследовании устойчивости систем управления высших порядков [15, 16]. |
