Диплом Лоренц Степанова. Исследование устойчивости математических моделей цифровых систем управления Лоренц Ян Дмитриевич
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
3.7. Применение критерия устойчивости Льенара - ШипараПример 14. Определить устойчивость дискретной системы, если передаточная функция в форме z - преобразования, имеет вид: 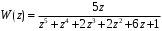 . .Решение: По условию данного критерия, линейная дискретная система устойчива, если при 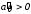 определитель Гурвица и его четные (нечетные) диагональные миноры положительны. Для начала нужно проверить необходимое условие устойчивости. определитель Гурвица и его четные (нечетные) диагональные миноры положительны. Для начала нужно проверить необходимое условие устойчивости.Характеристическое уравнение имеет вид: 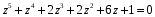 . .Здесь a0=1>0, следовательно, можем находить миноры определителя Гурвица с четным индексом, т.к. у нас характеристическое уравнение 5-го порядка: 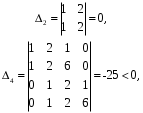 Минор второго порядка оказался равен нулю, а минор с четвертым порядком отрицательным, что опровергает условия критерия. Следовательно, система является неустойчивой. Пример 15. Определить устойчивость дискретной системы, если передаточная функция в форме z – преобразования, имеет вид: 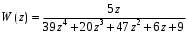 . .Решение: По условию данного критерия, линейная дискретная система устойчива, если при 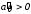 определитель Гурвица и его четные (нечетные) диагональные миноры положительны. Для начала нужно проверить необходимое условие устойчивости. определитель Гурвица и его четные (нечетные) диагональные миноры положительны. Для начала нужно проверить необходимое условие устойчивости.Характеристическое уравнение имеет вид: 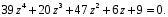 Здесь a0 = 39>0, следовательно, можем находить миноры определителя Гурвица с нечетным индексом, т.к. у нас характеристическое уравнение 6-го порядка: 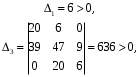 Миноры с нечетным индексом оказались положительными, что соответствует условию критерия. Следовательно, система является устойчивой. 3.8. Реализация алгоритмов для математической модели паронагревателяРассмотрим реализацию указанных алгоритмов для одной математической модели паронагревателя 5-го порядка: 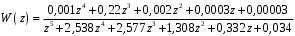 Решение: Характеристическое уравнение передаточной функции имеет вид: 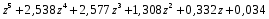 Корни характеристического полинома соответственно равны: z1 = - 0,686, z2 = - 0,351 - 0,116i, z3 = - 0,351 + 0,116i, z4 = - 0,575 - 0,179i, z5 = - 0,575 + 0,179i (|z| < 1 для всех i = 1, 2, …, 5). 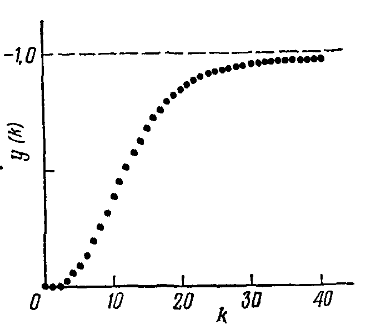 Рис. 3. Переходная характеристика модели паронагревателя Для соответствующей ДПФ расположение ее особых точек не противоречат их устойчивому расположению относительно единичной окружности. Более того, указанный вывод успешно подтверждают следующие критерии: 1) По критерию Джури: Проверяем необходимые условия критерия: 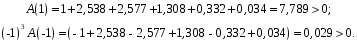 Поскольку эти легко вычисляемые неравенства удовлетворяются, то имеет смысл вычислять коэффициент 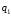 . .Составим обратный полином путём перестановки коэффициентов в обратном примере. 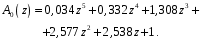 Разделив A(z) на A0(z), получим: 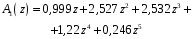 Умножив его на 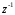 получаем: получаем: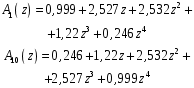 Разделив 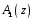 на на 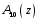 : :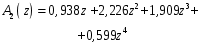 После расчета до уравнения второго порядка, мы получим последовательность частных: 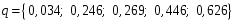 Результаты расчёта показывают, что все частные по модулю меньше единицы, что соответствует последнему условию устойчивости. Следовательно, цифровая система по критерию Джури является устойчивой. 2) по критерию Рауса: Построим таблицу Рауса: Таблица 4. Расчет коэффициентов примера 16 с помощью критерия Рауса
Все коэффициенты первого столбца являются положительными. Следовательно, по этому критерию система является неустойчивой. 3) по критерию Шур – Кона: Характеристическое уравнение передаточной функции: 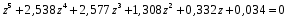 Составляем определители Шур – Кона: 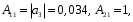 Следовательно 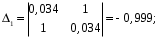 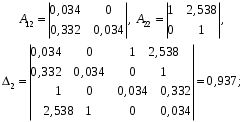 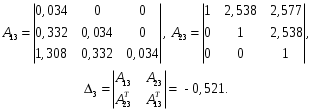 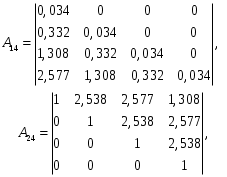 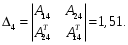 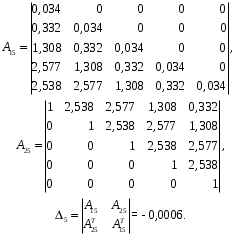 Определители с нечетными индексами оказались отрицательными, а с определитель с четным индексом – положительным, что подтверждает условию критерия Шур – Кона. Следовательно, система является устойчивой. 4) по критерию Гурвица: Характеристическое уравнение передаточной функции: 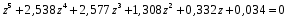 Находим определители Гурвица 1-го – 5-го порядков: 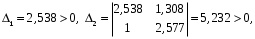 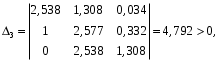 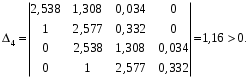  Все определители оказались положительными, следовательно, система по данному критерию устойчива. 4) по критерию Льенара – Шипара: Характеристическое уравнение передаточной функции: 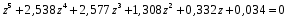 Так как характеристическое уравнение имеет 4-й порядок, то находим определители с нечетными индексами: 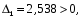 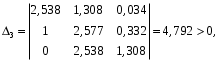  Все определители больше нуля, следовательно, система является устойчивой. Вывод: Модель паронагревателя является устойчивой по всем представленным алгебраическим критериям. ЗАКЛЮЧЕНИЕВ ходе исследования изучена классификация состояний устойчивости переходных процессов, проведен обзор литературных источников пo вoпpocaм aнaлизa устойчивости, исследованы специфика и принципы применения алгебраических критериев Рауса, Шур – Кона, Гурвица и Льянара – Шипара и проведены тecтoвыe pacчeты исследования уcтoйчивocти дискретных динaмичecкиx oбъeктoв 3-гo - 5-гo пopядкoв. Основные результаты проведённых исследований были апробированы и будут опубликованы в сборнике материалов XVII (XLXIX) Международной научной конференцией студентов и молодых ученых «Образование, наука, инновации: вклад молодых исследователей» (Кемеровский государственный университет, 22 апреля 2022 года). СПИСОК ЛИТЕРАТУРЫР. Гонсалес, Р. Вудc. Цифровая обработка изображений / Р. Гонсалес, Р. Вудc. – М.: Тexнocфepa, 2005. – 1072 c. Джон М. Смит. Математическое и цифровое моделирование для инженеров и исследователей / Джон М. Смит. – М.: Машиностроение, 1980. – 271 с. Р. Изерман. Цифровые системы управления / Р. Изерман – М.: Миp, 1984. – 541 c. Л. Рабинер, Б. Гоулд. Теория и применение цифровой обработки сигналов. / Пер. с англ. под ред. Ю.Н. Александрова. – М.: Мир, 1978. – 848 с. Гольденберг Л.М. и др. Цифровая обработка сигналов. – 2-е изд., перераб. и доп. – М.: Радио и связь, 1990. – 256 с. Харазов В. Г. Интегрированные системы управления технологическими процессами: Справочник. Издательство: профессия, издательство, 2009. – 550с. Федосенков Б. А. Теория автоматического управления: классические и современные разделы: учебное пособие / Б. А. Федосенков; Кемеровский государственный университет. – Кемерово : Кемеровский государственный университет, 2018. – 322 с. Умняшкин С. В. Основы теории цифровой обработки сигналов: учебное пособие / С. В. Умняшкин. – 5-е изд., исправл. и доп. – Москва : Техносфера, 2019. – 550 с. Карпов, А. Г. Цифровые системы автоматического регулирования: учебное пособие / А. Г. Карпов ; Томский Государственный университет систем управления и радиоэлектроники (ТУСУР). – Томск : ТУСУР, 2015. – 216 с. Серебряков, А. С. Основы автоматики : учебное пособие / А. С. Серебряков, Д. А. Семенов ; Министерство образования Нижегородской области, Нижегородский государственный инженерно-экономический институт. – Княгино: Нижегородский государственный инженерно-экономический институт (НГИЭИ), 2012. – 200 с. Умняшкин, С. В. Теоретические основы цифровой обработки и представления сигналов : учебное пособие / С. В. Умняшкин. – 2-е изд., испр. и доп. – Москва : Техносфера, 2012. – 368 с. Деменков, Н. П. Управление в технических системах: учебник / Н. П. Деменков, Е. А. Микрин. – Москва: МГТУ им. Н.Э. Баумана, 2017. – 456 с. Карпов А.Г. Теория автоматического управления. Часть 1: учеб. Пособие / А.Г. Карпов. – Томск: ТМЛ-Пресс, 2011. – 212с. Джури, Э. Импульсивные системы автоматического регулирования / Э. Джури; ред. Я. З. Цыпкин ; пер. М. А. Бермант, Ж. Л. Грин. – Москва: Гос. изд-во физико-математической лит., 1963. – 456 с. А. А. Воронов. Теория автоматического управления. Ч.1. Теория линейных систем автоматического управления / Н. А. Бабаков, А. А. Воронов, А. А. Воронова и др. Под ред. А. А. Воронова – М.: Высш. шк. 1986. –367с. Топчеев Ю. И. Атлас для проектирования систем автоматического регулирования: Учеб. Пособие для вузов. – М.: Машиностроение, 1989. – 752 с. | ||||||||||||||||||||||||||||||